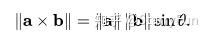向量的叉乘 a ^ b
高中数学中我们可以得到公式 a * b = |a| * |b| * sin<a,b>
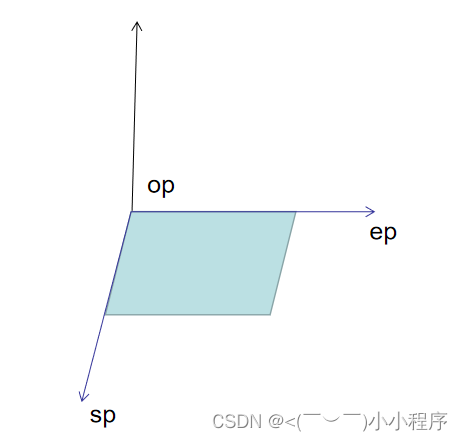
可以使用叉乘获取两个向量的左右位置,如下图所示
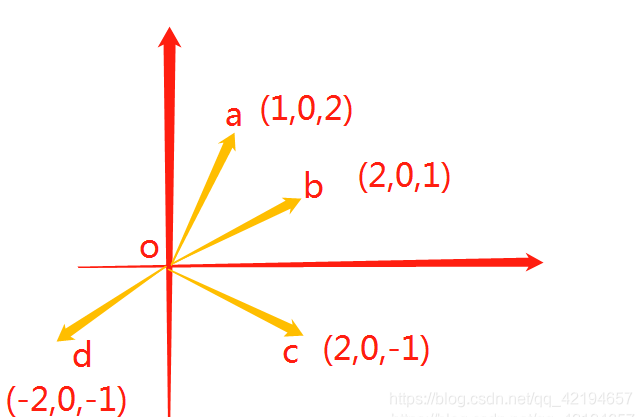
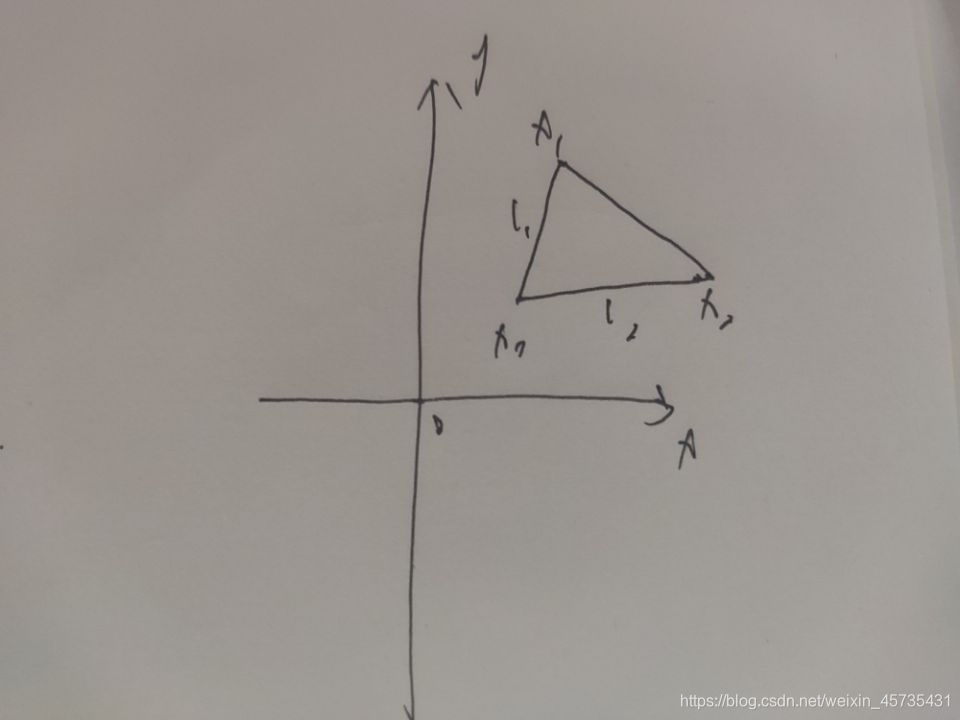
案例一(案例中将y去掉,相当于俯视坐标系之后x,z):
Vector3 a = new Vector3 (1,0,2);Vector3 b = new Vector3 (2,0,1);Vector3 c = new Vector3 (2,0,-1);Vector3 d = new Vector3 (-2,0,-1);// Use this for initializationvoid Start () {Debug.LogError(Vector3.Angle(a,b));//36.8699Debug.LogError(Vector3.Cross(a,b).y);//3Debug.LogError(Vector3.Cross(b,d).y);//0Debug.LogError(Vector3.Cross(a,c).y);//5Debug.LogError(Vector3.Cross(a,d).y);//-3}
上面的代码中我们可以看出来 ∠aob = 36.8699°
根据点乘公式:向量a * 向量b = |a| * |b| * sin36.8699° = 根5 * 根5 * sin36.8699° = 3;