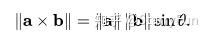这两天纠结一个问题,矢量叉乘能否反求矢量?
a ⃗ × b ⃗ = c ⃗ \vec{a}\times\vec{b}=\vec{c} a×b=c
如果已经知道矢量 a ⃗ \vec{a} a和矢量 c ⃗ \vec{c} c,能否求解得到矢量 b ⃗ \vec{b} b呢?
想了很久,答案是不行的, a ⃗ × b ⃗ = c ⃗ \vec{a}\times\vec{b}=\vec{c} a×b=c可以看作 [ a ] b ⃗ = c ⃗ [a]\vec{b}=\vec{c} [a]b=c,也即
[ 0 − a z a y a z 0 − a x − a y a x 0 ] [ b x b y b z ] = [ c x c y c z ] \begin{bmatrix} 0& -a_z & a_y\\ a_z&0 & -a_x\\ -a_y&a_x &0\end{bmatrix} \begin{bmatrix}b_x\\b_y\\b_z\end{bmatrix} =\begin{bmatrix}c_x\\c_y\\c_z\end{bmatrix} ⎣⎡0az−ay−az0axay−ax0⎦⎤⎣⎡bxbybz⎦⎤=⎣⎡cxcycz⎦⎤
相当于求解一个线性方程组,由于 [ a ] [a] [a]的行列式 d e t [ a ] = 0 det[a]=0 det[a]=0,所以 b ⃗ \vec{b} b至少是没有唯一解的。
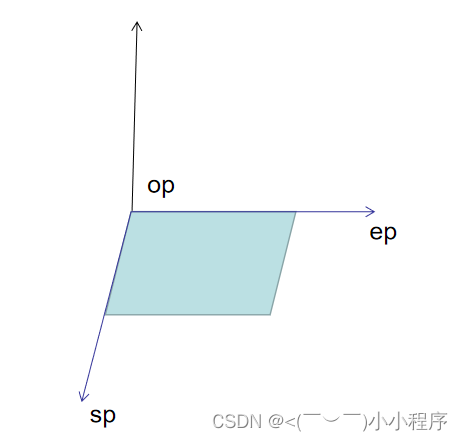
从几何直观上也非常好解释,矢量 a ⃗ \vec{a} a要找一个矢量 b ⃗ \vec{b} b让它们张成的平面的法向矢量等于 c ⃗ \vec{c} c,是可以找无数个的。

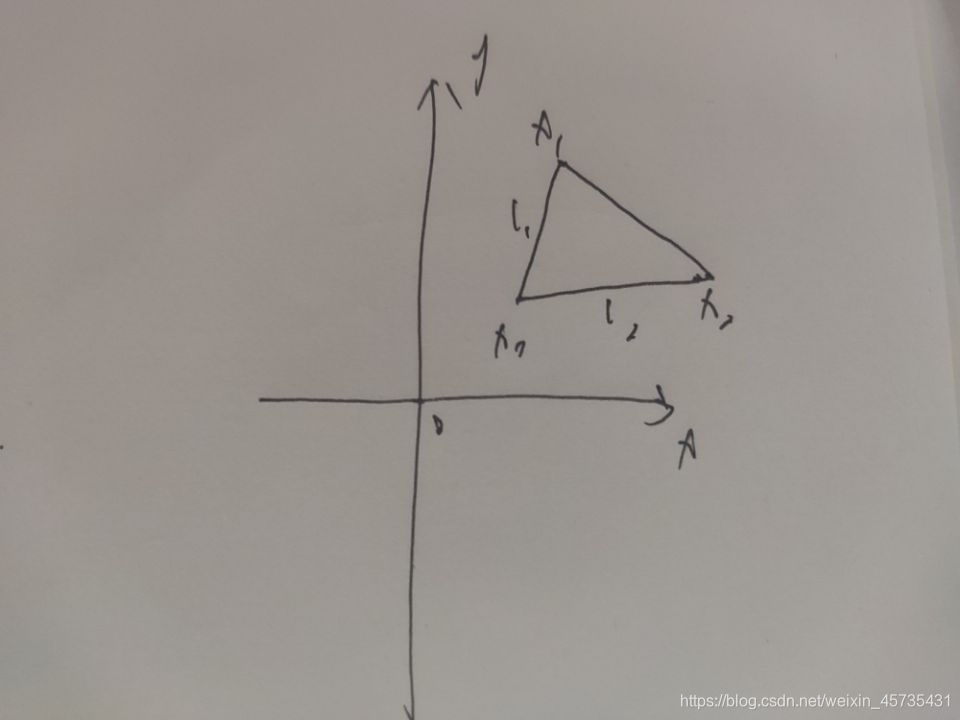
矢量 a ⃗ \vec{a} a和矢量 b ⃗ \vec{b} b在同一平面,确定唯一方向的矢量 c ⃗ \vec{c} c,矢量 c ⃗ \vec{c} c的大小等于矢量 a ⃗ \vec{a} a和矢量 b ⃗ \vec{b} b构成的三角形的面积,如上图所示可以有 b 1 b1 b1、 b 2 b2 b2、 b 3 b3 b3多个矢量可以选择,保证三角形的面积是恒定的,所以解是不唯一的。
放在实际的应用中,线速度等于角速度叉乘矢径。
r ⃗ ˙ = ω ⃗ × r ⃗ {\dot{\vec{r}}}=\vec{\omega}\times\vec{r} r˙=ω×r
知道线速度和矢径,也是无法求出角速度的。