今天刚开始做向量题，碰到下面这题

解析如下

哥们感觉解释的很笼统，也不是很能理解，在查阅了各种资料以及拿餐巾纸叠来叠去以后终于搞明白了，总结如下：

首先，题目的意思是：

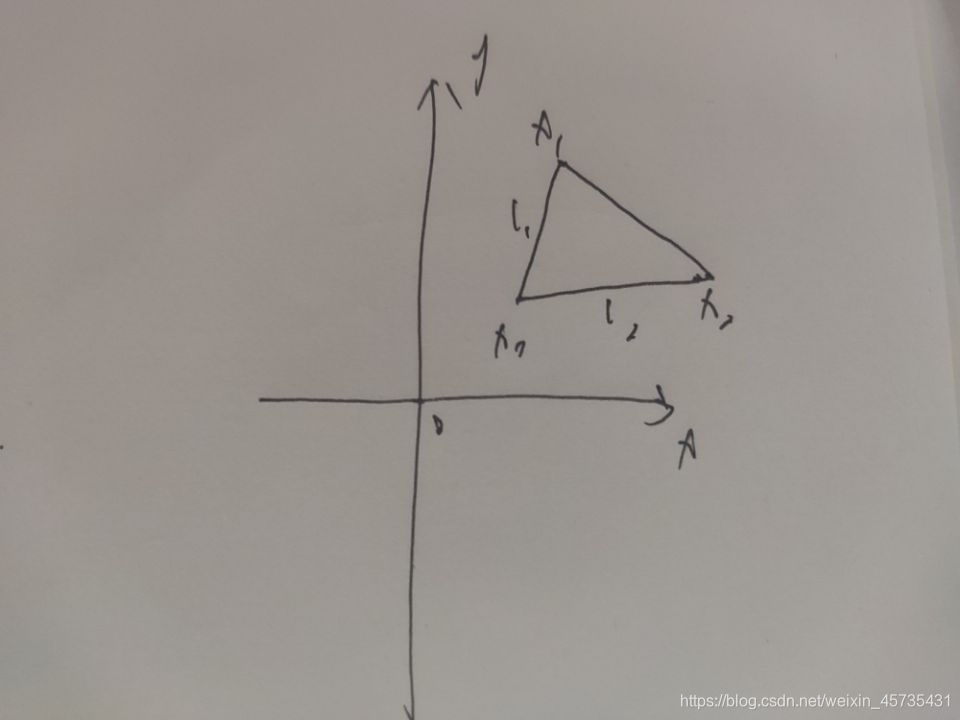
直线L为两个平面的交线，与另一个平面π随意交于一个点M，然后在平面π内，过M点做直线L₁，L₁与直线L垂直，求L₁

思路分析：我们首先画一个平面π，然后任意定一个点M，过M任意画一条直线L，再在平面π中，过M取一条唯一能和直线L垂直的直线L₁

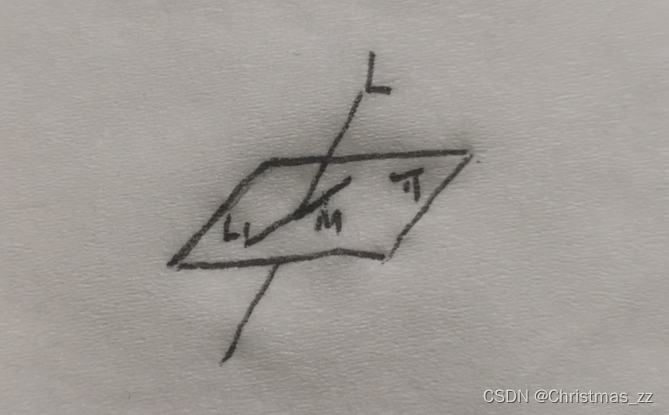
有一说一哥们画的真的很生动，看不明白的扣yzz

接着分析：图是画出来了，那怎么求L₁这条直线呢？该题目中我们可以很容易的联立三个平面把M点坐标求出来，是（0，-1，0），有交点的情况下就可以考虑使用点向式方程来求直线的解析式：

那现在问题的矛头就指向了求直线L₁的方向向量，这就是我疑惑开始的地方，上面的解析中，L₁的方向向量是通过平面π的法向量和L的方向向量的向量叉乘得到的，为啥呢？再往上看，L的方向向量为啥由确定L的两个平面的法向量叉乘得到的呢？

这里就是一个需要关键理解的地方：向量叉乘的几何意义是什么？

网上有很多说法，比如为了维护乘法交换律结合律啥的，有点没看懂，但是有一个人提到了从平面角度去理解，说向量叉乘的结果可以理解为由这两个向量叉乘的模所得到的平行四边形的面积，再往大了说就是，两个向量叉乘可以唯一确定一个平面，而在这时标志一个平面的唯一关键因素就是这个平面的法向量，所以两个向量的叉乘的方向是得到的平面的法向量，方向就是通过右手定则来定。这一点很重要，换个说法来理解：如果我们想得到一条和已知两个向量都垂直的向量，让他们叉乘就OK了。

带着这个思路再来看一下这题，我们要求L₁的方向向量，已知L₁的方向向量必和平面π的法向量垂直，又已知L₁的方向向量和L的方向向量垂直，所以L₁的方向向量就是这两个垂直向量的叉乘，那现在的矛头就又指向了求L的方向向量，那么现在就很简单了，L是两个平面的交线，所以必和那两个平面的法向量垂直，所以L的方向向量就是那两个平面的法向量的叉乘，这题就解决了。

当然啊可能本身只是一道很简单的题被哥们想复杂了，如果有哪里讲的不对的或要改进的地方一定要告诉我。