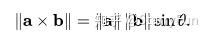矢量叉乘，向量外积

原创不易，路过的各位大佬请点个赞

1. 矢量叉乘定义

定义两个向量$\mathbf{a}$和$\mathbf{b}$，他们的叉乘可以写为
$$\mathbf{a}\times \mathbf{b}$$

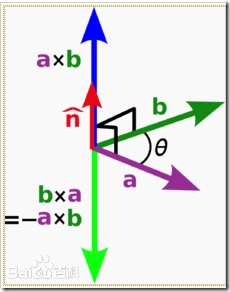
本质上向量叉乘为向量旋转，满足右手螺旋准则；
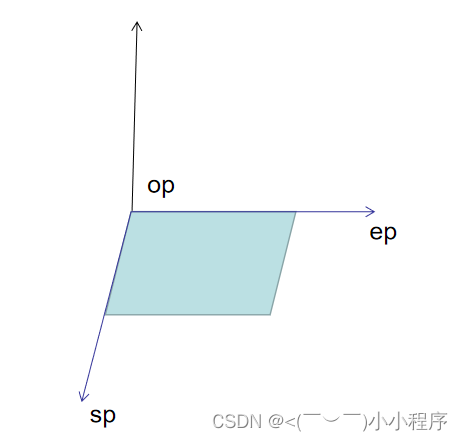
叉乘结果是一个向量，向量模长是向量A，B组成平行四边形的面积；向量方向是垂直于向量A,B组成的平面；也叫向量积

与点乘不同之处是：点乘结果是一个数，表示两个向量的投影关系，也叫数量积
$$\mathbf{a}\cdot \mathbf{b}=|\mathbf{a}||\mathbf{b}|\cos \theta$$

2. 模长

$$|\mathbf{c}|=|\mathbf{a}\times \mathbf{b}|=|\mathbf{a}||\mathbf{b}|\sin \theta$$
$|\mathbf{c}|$长度在数值上等于以$\mathbf{a}$，$\mathbf{b}$，夹角为θ组成的平行四边形的面积。
而c的方向垂直于$\mathbf{a}$与$\mathbf{b}$所决定的平面，$\mathbf{c}$的指向按右手定则从a转向b来确定。

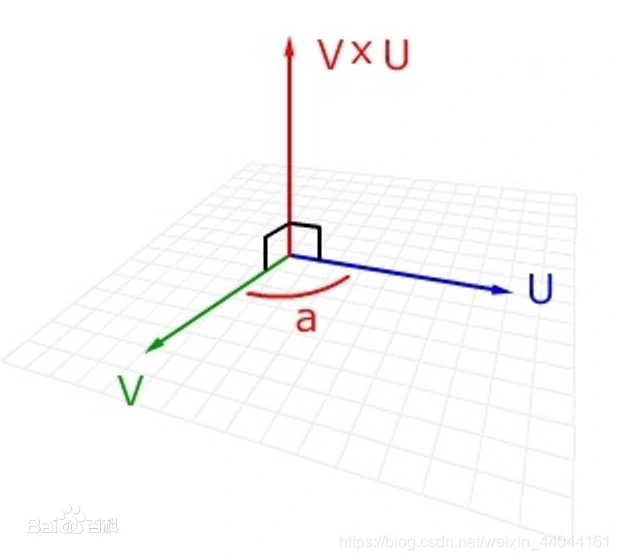
3. 方向

$\mathbf{a}$向量与$\mathbf{b}$向量的向量积的方向与这两个向量所在平面垂直，且遵守右手定则。（一个简单的确定满足“右手定则”的结果向量的方向的方法是这样的：若坐标系是满足右手定则的，当右手的四指从$\mathbf{a}$以不超过180度的转角转向b时，竖起的大拇指指向是$\mathbf{c}$的方向。）

4. 坐标运算

向量$\mathbf{a}$的坐标表示
$$\mathbf{a}=(a_x,a_y,a_z)$$
向量$\mathbf{a}$的坐标轴矢量表示
$$\mathbf{a}=a_{x}i+a_{y}j+a_{z}k$$

其中矢量的x轴、y轴、z轴的单位矢量i、j、k、满足以下关系

$$\begin{gathered} i\times j=k=-j\times i \\ j\times k=i=-k\times j \\ k\times i=j=-i\times k \\ i\times i=j\times j=k\times k=0 \end{gathered}$$
其中的0为零矢量。
附加点乘的运算规则
$$\begin{gathered} i\cdot j=k=-j\times i \\ j\cdot k=i=-k\cdot j \\ k\cdot i=j=-i\cdot k \\ i\cdot i=j\cdot j=k\cdot k=1 \end{gathered}$$

$$\begin{array}{rl}\mathbf{a}\times \mathbf{b}& =\left|\begin{array}{ccc}i& j& k\\ a_x& a_y& a_z\\ b_x& b_y& b_z\end{array}\right|\\ & =\left|\begin{array}{cc}{a}_y& a_z\\ b_y& b_z\end{array}\right|i-\left|\begin{array}{cc}{a}_x& a_z\\ b_x& b_z\end{array}\right|j+\left|\begin{array}{cc}{a}_x& a_y\\ b_x& b_y\end{array}\right|k\\ & =(a_y{b}_z-a_z{b}_y)i+(a_z{b}_x-a_x{b}_z)j+(a_x{b}_y-a_y{b}_x)k\end{array}$$

6. 叉乘矩阵（斜对称矩阵）

每一个矢量都一个对应的斜对称矩阵，$\mathbf{a}$
$$[\mathbf{a}\times ]=\left[\begin{array}{ccc}0& -a_y& a_z\\ a_y& 0& -a_x\\ -a_z& a_x& 0\end{array}\right]$$

则两个矢量的叉乘可以写为
$$\begin{array}{rl}\mathbf{a}\times \mathbf{b}& =[\mathbf{a}\times ]\mathbf{b}\\ & =\left[\begin{array}{ccc}0& -a_y& a_z\\ a_y& 0& -a_x\\ -a_z& a_x& 0\end{array}\right]\left[\begin{array}{c}{b}_x\\ b_y\\ b_z\end{array}\right]\end{array}$$

性质：（$A=[\mathbf{a}\times ]$）
1- $A^T=-A$
2- $A$，$B$为斜对称矩阵，则$A+B$为斜对称矩阵
3- $k$为偶数，$A^k$为对称矩阵； $k$为奇数，$A^k$为斜对称矩阵；

6. 叉乘运算规则

1、交换律： $a\times b=-b\times a$

2、分配律： $a\times （b+c)=a\times b+a\times c$

3、与标量r相乘： $ra\times b=r(a\times b)$

4、不满足结合律，但满足雅可比恒等式：： $a\times （b\times c）+b\times （c\times a）+c\times （a\times b）=0$。

5 、 两个非零向量a和b平行，当且仅当$a\times b=0$。

6、 拉格朗日公式
$（a\times b）\times c=b（a\cdot c）-a（b\cdot c）$
$a\times （b\times c）=b（a\cdot c）-c（a\cdot b）$
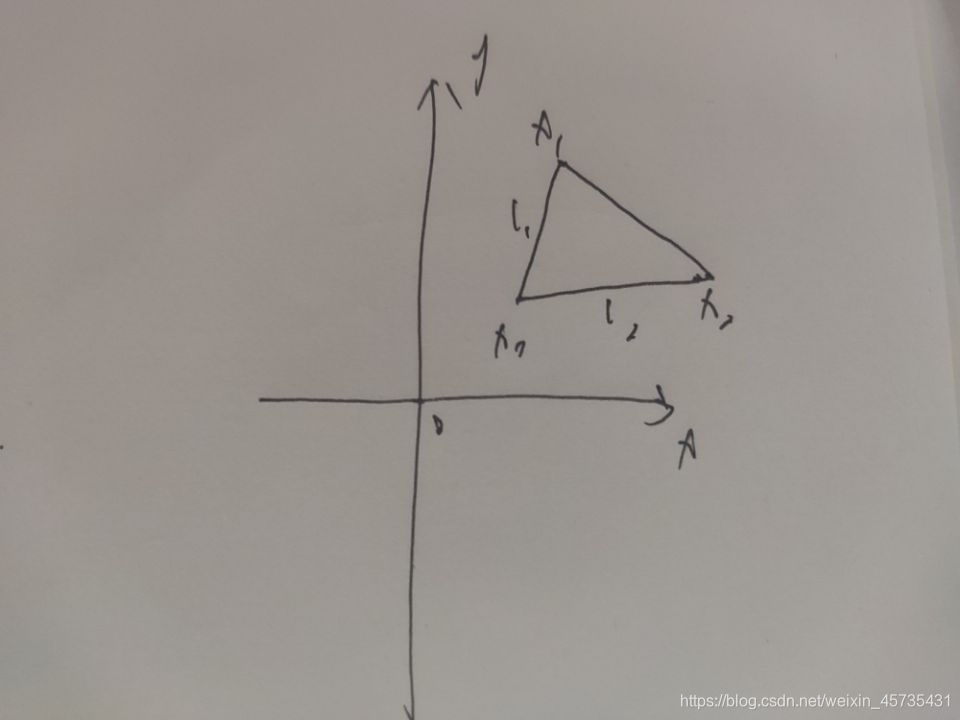
证明如下图

原创不易，路过的各位大佬请点个赞