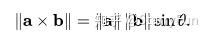点乘与叉乘

article/2025/10/14 8:53:25

0. 几何含义

0.1 点乘

点乘，又称向量的内积，结果为一个数，计算公式如下：

上述公式的推导过程如下：

因此，通过点乘可以得出两个向量之间的夹角，向量垂直时，点乘结果为0.

0.2 叉乘

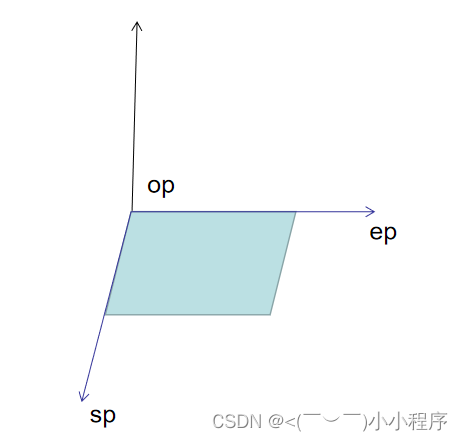
叉乘，又称向量的外积，运算结果为一个向量，该向量z与向量a，b组成的平面垂直，计算公式如下：

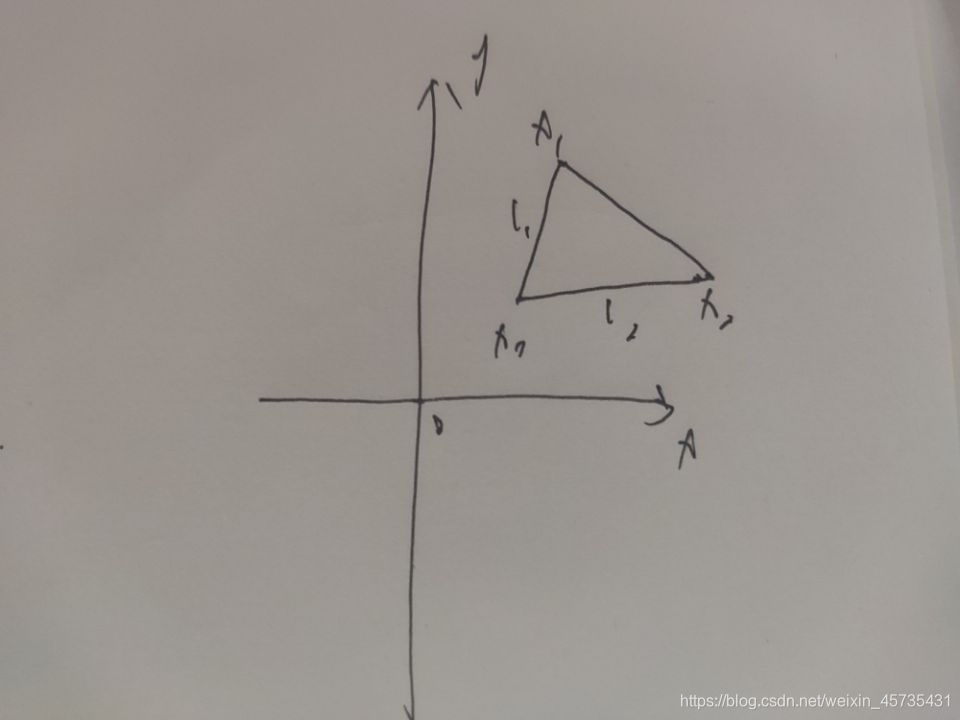
向量叉乘得到是向量组成平面的法向量，法向量行列式的值可以解释为这两个向量a, b共起点时，所构成平行四边形的面积。

1. numpy实现

1.1 向量点乘

numpy中使用dot函数来完成向量之间的点乘（对应元素相乘再相加）

1.2 矩阵点乘

numpy中使用multiply函数来实现矩阵之间的点乘（对应位置元素相乘），也可使用 * 运算符实现相同的功能。此时两个矩阵的尺寸大小必须相等。

1.3 矩阵叉乘

numpy中使用matmul函数来实现矩阵之间的叉乘（对应位置元素相乘），也可使用 @ 运算符实现相同的功能。此时第一个矩阵的列数等于第二个矩阵的行数。

总结：

对于向量，使用dot函数完成向量的点乘

对于矩阵，使用multiply函数和 * 运算符完成矩阵的点乘，使用matmul函数和@运算符完成矩阵的叉乘。

2. pytorch实现

2.1 矩阵点乘

pytorch中使用mul函数来完成二维矩阵之间的点乘，同时 * 运算符也可实现相同的功能。

>>> x
tensor([[-0.9263,  0.3411, -0.0781, -0.9598],[-1.1215,  0.9547, -0.2663,  0.6355],[-0.2772,  0.2032, -1.4178, -1.8679]])
>>> torch.ones([3, 4])
tensor([[1., 1., 1., 1.],[1., 1., 1., 1.],[1., 1., 1., 1.]])
>>> y = torch.ones([3, 4]) 
>>> x * y
tensor([[-0.9263,  0.3411, -0.0781, -0.9598],[-1.1215,  0.9547, -0.2663,  0.6355],[-0.2772,  0.2032, -1.4178, -1.8679]])
>>> torch.mul(x, y)
tensor([[-0.9263,  0.3411, -0.0781, -0.9598],[-1.1215,  0.9547, -0.2663,  0.6355],[-0.2772,  0.2032, -1.4178, -1.8679]])

2.2 矩阵叉乘

pytorch中使用mm函数来完成二维矩阵之间的叉乘，同时@运算符【具体对应的函数应该是matmul】也可完成矩阵的叉乘

pytorch中matmul函数是一个神奇的函数根据第一个和第二个输入tensor的维度得到的是不同的效果。具体介绍如下图所示：

假设两个tensor都是一维向量，那么返回的结果是向量之间的点乘，即一个值
假设两个tensor都是二维矩阵，那么返回的结果是矩阵的叉乘
假设第一个tensor是一维向量，第二个tensor是二维矩阵，那么会给第一个tensor扩充一个维度，从而实现矩阵叉乘（一维向量的维度与二维矩阵的行数相等），得到结果之后将扩充的维度去除
假设第一个tensor是二维矩阵，第二个tensor是一维向量，与上面类似，扩充维度之后进行矩阵叉乘，得到结果

上述不同情形的具体过程可以用下图表示：

此外，matmul函数实现了多维情况下矩阵的乘法，例如，输入的第一个tensor的维度为【k, m, p】，第二个tensor的维度为【k, p, n】，则最后的结果维度为【k，m，n】，即对于通道上的两个矩阵完成叉乘，然后组合在一起。

3. matmul函数实现协方差batch计算

协方差（Covariance）在概率论和统计学中用于衡量两个变量的总体误差。而方差是协方差的一种特殊情况，即当两个变量是相同的情况。计算公式如下：

对于矩阵

根据协方差矩阵的定义: 协方差矩阵的每个元素是各个向量元素之间的协方差.可以得到对应的协方差矩阵求法如下：

矩阵中的数据按行排列与按列排列求出的协方差矩阵是不同的，默认情况下按行排列。即每一行是一个observation(or sample)，那么每一列就是一个随机变量。

$X_{m\times{n}}=\begin{bmatrix}a_{11} &a_{12} &\cdots &a_{1n} \\ a_{21} &a_{22} &\cdots &a_{2n} \\ \vdots &\vdots & \vdots& \vdots \\a_{m1} &a_{m2} &\cdots &a_{mn} \\ \end{bmatrix}=\begin{bmatrix}c_1 &c_2 &\cdots&c_n \\ \end{bmatrix}$

对应的协方差矩阵为：

$covMatrix = \frac{1}{m-1}\begin{bmatrix}cov(c_1,c_1) &cov(c_1,c_2) &\cdots &cov(c_1,c_n) \\ cov(c_2,c_1) &cov(c_2,c_2) &\cdots &cov(c_2,c_n) \\ \vdots &\vdots &\vdots &\vdots \\ cov(c_n,c_1) &cov(c_n,c_2) &\cdots &cov(c_n,c_n) \end{bmatrix}$

示例中，矩阵的维度为【m, n】表示m个样本，每个样本包含n个特征，最后得到的协方差矩阵维度为【n, n】。

numpy中提供函数cov来协方差矩阵，具体用法如下：

其中需要注意重要的参数rowvar的含义：

使用cov函数来求协方差矩阵，默认情况下是按列排列，即每一行代表一个变量，而每一列代表一个sample（观测点）。即输入矩阵的维度【m,n】，输出的协方差矩阵维度【m,m】。

>>> import torch 
>>> x = torch.randn([3, 4]) 
>>> x
tensor([[-0.9263,  0.3411, -0.0781, -0.9598],[-1.1215,  0.9547, -0.2663,  0.6355],[-0.2772,  0.2032, -1.4178, -1.8679]])
>>> np.cov(x.numpy())
array([[ 0.41436621,  0.28581725,  0.2887559 ],[ 0.28581725,  0.87789806, -0.04488792],[ 0.2887559 , -0.04488792,  0.93183437]])

当输入维度扩充到三维时，在numpy中需要利用for循环来遍历，然后组合，这样的时间效率较差，因此可以通过torch中提供的matmul函数来实现三维下的协方差矩阵求法。

def cov_matrix(tensor, rowvar=True):# 输入为【batch, m个特征，n个样本】 输出【batch, m, m】tensor = tensor if rowvar else tensor.transpose(-1, -2)tensor = tensor - tensor.mean(dim=-1, keepdim=True)factor = 1/ (tensor.shape[-1] - 1)return factor * tensor @ tensor.transpose(-1, -2)