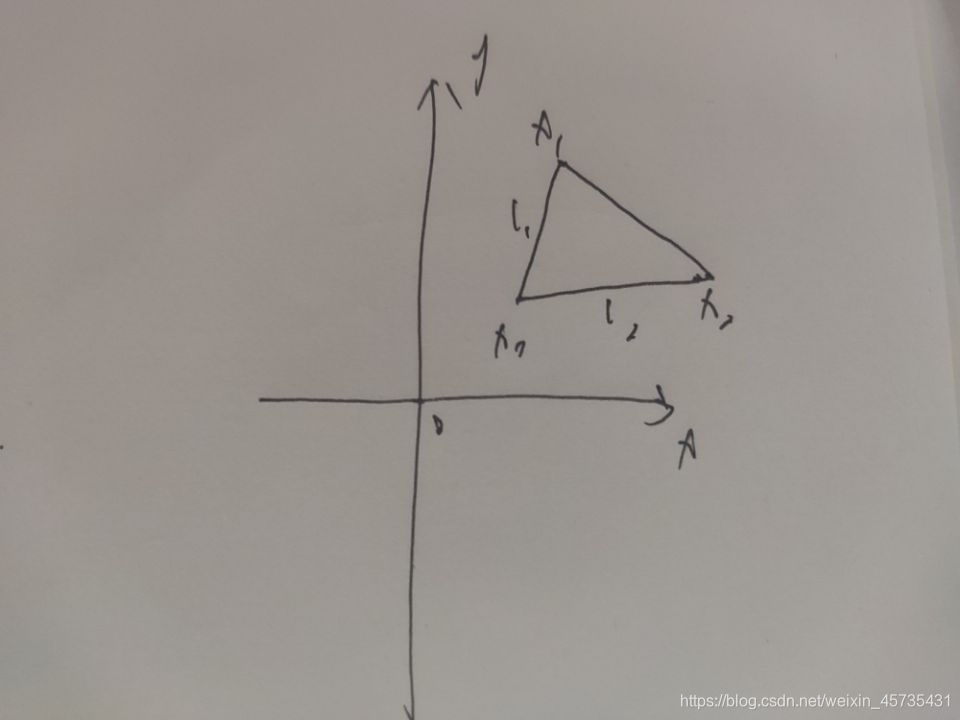
叉乘计算公式几何推导
推导方法1

经过旋转变换之后,对象的面积是不会改变的。
把 △ F E G \triangle{FEG} △FEG旋转 θ \theta θ到 △ F ′ E G ′ \triangle{F'EG'} △F′EG′
△ F ′ E G ′ \triangle{F'EG'} △F′EG′的面积计算是简单的,即F’的纵坐标 乘以G’的横坐标
首先计算出F’ G’的坐标
F ′ ( x , y ) = [ x 1 y 1 ] [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] = [ x 1 cos ( θ ) + y 1 sin ( θ ) − x 1 sin ( θ ) + y 1 cos ( θ ) ] F'(x, y) = \left[\begin{matrix}x_{1} & y_{1}\end{matrix}\right] \left[\begin{matrix}\cos{\left (\theta \right )} & - \sin{\left (\theta \right )}\\\sin{\left (\theta \right )} & \cos{\left (\theta \right )}\end{matrix}\right] = \left[\begin{matrix}x_{1} \cos{\left (\theta \right )} + y_{1} \sin{\left (\theta \right )} & - x_{1} \sin{\left (\theta \right )} + y_{1} \cos{\left (\theta \right )}\end{matrix}\right] F′(x,y)=[x1y1][cos(θ)sin(θ)−sin(θ)cos(θ)]=[x1cos(θ)+y1sin(θ)−x1sin(θ)+y1cos(θ)]
G ′ ( x , y ) = [ x 2 y 2 ] [ cos ( θ ) − sin ( θ ) sin ( θ ) cos ( θ ) ] = [ x 2 cos ( θ ) + y 2 sin ( θ ) − x 2 sin ( θ ) + y 2 cos ( θ ) ] G'(x, y) = \left[\begin{matrix}x_{2} & y_{2}\end{matrix}\right] \left[\begin{matrix}\cos{\left (\theta \right )} & - \sin{\left (\theta \right )}\\\sin{\left (\theta \right )} & \cos{\left (\theta \right )}\end{matrix}\right] = \left[\begin{matrix}x_{2} \cos{\left (\theta \right )} + y_{2} \sin{\left (\theta \right )} & - x_{2} \sin{\left (\theta \right )} + y_{2} \cos{\left (\theta \right )}\end{matrix}\right] G′(x,y)=[x2y2][cos(θ)sin(θ)−sin(θ)cos(θ)]=[x2cos(θ)+y2sin(θ)−x2sin(θ)+y2cos(θ)]
2 S F ′ E G ′ = G x ′ ⋅ F y ′ = ( − x 1 sin ( θ ) + y 1 cos ( θ ) ) ∗ ( x 2 cos ( θ ) + y 2 sin ( θ ) ) 2S_{F'EG'} = G_x' \cdot F_y' = (- x_{1} \sin{\left (\theta \right )} + y_{1} \cos{\left (\theta \right )} ) * (x_{2} \cos{\left (\theta \right )} + y_{2} \sin{\left (\theta \right )} ) 2SF′EG′=Gx′⋅Fy′=(−x1sin(θ)+y1cos(θ))∗(x2cos(θ)+y2sin(θ))
= − x 1 x 2 sin ( θ ) cos ( θ ) − x 1 y 2 sin 2 ( θ ) + x 2 y 1 cos 2 ( θ ) + y 1 y 2 sin ( θ ) cos ( θ ) = - x_{1} x_{2} \sin{\left (\theta \right )} \cos{\left (\theta \right )} - x_{1} y_{2} \sin^{2}{\left (\theta \right )} + x_{2} y_{1} \cos^{2}{\left (\theta \right )} + y_{1} y_{2} \sin{\left (\theta \right )} \cos{\left (\theta \right )} =−x1x2sin(θ)cos(θ)−x1y2sin2(θ)+x2y1cos2(θ)+y1y2sin(θ)cos(θ)
= − x 1 x 2 2 y 2 x 2 2 + y 2 2 − x 1 y 2 3 x 2 2 + y 2 2 + x 2 3 y 1 x 2 2 + y 2 2 + x 2 y 1 y 2 2 x 2 2 + y 2 2 = - \frac{x_{1} x_{2}^{2} y_{2}}{x_{2}^{2} + y_{2}^{2}} - \frac{x_{1} y_{2}^{3}}{x_{2}^{2} + y_{2}^{2}} + \frac{x_{2}^{3} y_{1}}{x_{2}^{2} + y_{2}^{2}} + \frac{x_{2} y_{1} y_{2}^{2}}{x_{2}^{2} + y_{2}^{2}} =−x22+y22x1x22y2−x22+y22x1y23+x22+y22x23y1+x22+y22x2y1y22
= − x 1 y 2 + x 2 y 1 = - x_{1} y_{2} + x_{2} y_{1} =−x1y2+x2y1
推导方法2

S A C G = S A H C + S H G C S_{ACG} = S_{AHC} + S_{HGC} SACG=SAHC+SHGC
S H G C = S G C B S_{HGC} = S_{GCB} SHGC=SGCB
S A B C = S A B C G − S A C G = S A B C G − S A H C − S H G C = S A B C G − S A H C − S G C B S_{ABC} = S_{ABCG} - S_{ACG} = S_{ABCG} - S_{AHC} - S_{HGC} = S_{ABCG} - S_{AHC} - S_{GCB} SABC=SABCG−SACG=SABCG−SAHC−SHGC=SABCG−SAHC−SGCB
= S A B G − S A H C = x 2 y 1 − x 1 y 2 = S_{ABG} - S_{AHC} = x_{2} y_{1} - x_{1} y_{2} =SABG−SAHC=x2y1−x1y2
推导方法3

S A B C = S A B E C − S B C E S_{ABC} = S_{ABEC} - S_{BCE} SABC=SABEC−SBCE
= 1 2 S D H C E + 1 2 S B E F G − S B C E = \frac{1}{2}S_{DHCE} + \frac{1}{2}S_{BEFG} - S_{BCE} =21SDHCE+21SBEFG−SBCE
= 1 2 S D H C E + 1 2 S B E F G − 1 2 S B E C I = \frac{1}{2}S_{DHCE} + \frac{1}{2}S_{BEFG} - \frac{1}{2}S_{BECI} =21SDHCE+21SBEFG−21SBECI
= 1 2 S D E F G I H = 1 2 ( S D E F A − S H A G I ) = \frac{1}{2}S_{DEFGIH} = \frac{1}{2}(S_{DEFA} - S_{HAGI}) =21SDEFGIH=21(SDEFA−SHAGI)
= 1 2 ( x 2 y 1 − x 1 y 2 ) = \frac{1}{2}(x_{2} y_{1} - x_{1} y_{2}) =21(x2y1−x1y2)
推导方法4

S A B C = S A B P + S A C P + S B C P S_{ABC} = S_{ABP} + S_{ACP} + S_{BCP} SABC=SABP+SACP+SBCP
= 1 2 ( S B P H D + S C P G F + S P B C E ) =\frac{1}{2}( S_{BPHD} + S_{CPGF} + S_{PBCE}) =21(SBPHD+SCPGF+SPBCE)
= 1 2 ( S A D E F − S A G P H ) =\frac{1}{2}( S_{ADEF} - S_{AGPH}) =21(SADEF−SAGPH)
= 1 2 ( x 2 y 1 − x 1 y 2 ) = \frac{1}{2}(x_{2} y_{1} - x_{1} y_{2}) =21(x2y1−x1y2)