叉乘分配律的几何证明
方法1
叉乘常被用于计算机图形学求平面法向量计算。
叉乘的物理意义可以理解成力矩。力是可以合成与分解的,所以叉乘当然支持分配律。
下面使用几何的方式证明:
( a ⃗ + b ⃗ ) × c ⃗ = a ⃗ × c ⃗ + b ⃗ × c ⃗ (\vec{a}+\vec{b}) \times \vec{c} = \vec{a} \times \vec{c} + \vec{b} \times \vec{c} (a+b)×c=a×c+b×c
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-JFmn8FKM-1612510802820)(geogebra-export.png)]

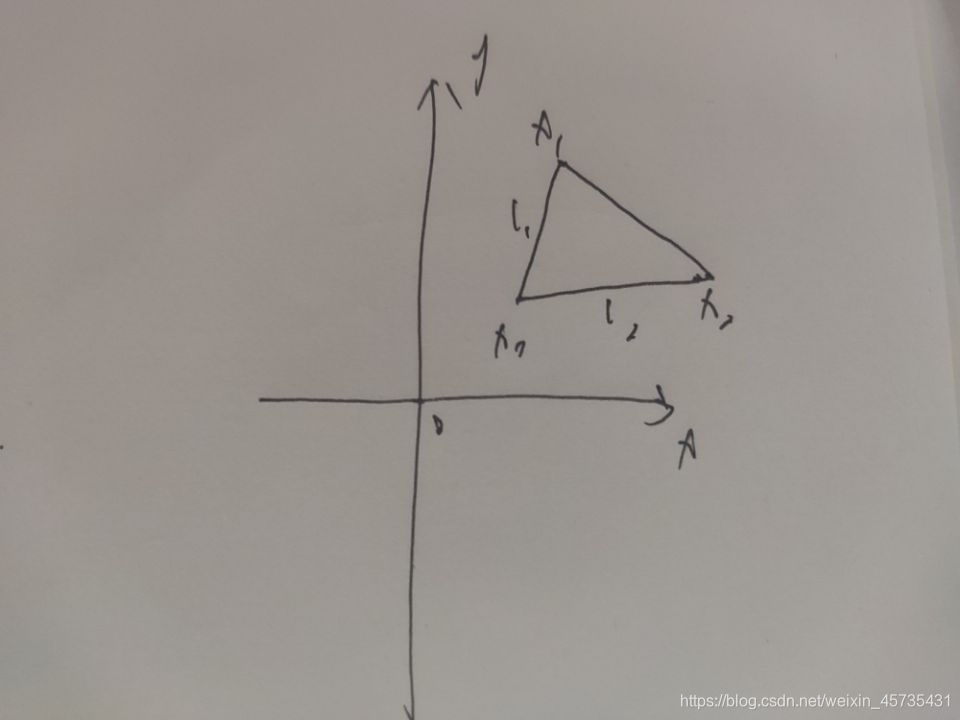
( a ⃗ + b ⃗ ) × c ⃗ = ( O A ⃗ + A F ⃗ ) × O C ⃗ = O F ⃗ × O C ⃗ = S O F E C ⋅ n 1 ⃗ (\vec{a}+\vec{b}) \times \vec{c} = (\vec{OA}+\vec{AF}) \times \vec{OC} = \vec{OF} \times \vec{OC} = S_{OFEC}\cdot \vec{n1} (a+b)×c=(OA+AF)×OC=OF×OC=SOFEC⋅n1
a ⃗ × c ⃗ = O A ⃗ × O C ⃗ = S O A D C ⋅ n 2 ⃗ \vec{a} \times \vec{c} = \vec{OA} \times \vec{OC} = S_{OADC}\cdot \vec{n2} a×c=OA×OC=SOADC⋅n2
b ⃗ × c ⃗ = A F ⃗ × O C ⃗ = S A F E D ⋅ n 3 ⃗ \vec{b} \times \vec{c} = \vec{AF} \times \vec{OC} = S_{AFED}\cdot \vec{n3} b×c=AF×OC=SAFED⋅n3
n 1 ⃗ , n 2 ⃗ , n 3 ⃗ \vec{n1}, \vec{n2}, \vec{n3} n1,n2,n3分别是平行四边形 O F E C , O A D C , A F E D OFEC,OADC,AFED OFEC,OADC,AFED的单位法向量
平面 O F E C , O A D C , A F E D OFEC,OADC,AFED OFEC,OADC,AFED恰好围成一个三棱柱, 将其以 O F E C OFEC OFEC为底平放,投影到三条平行棱的垂直平面后,得投影平面图:
投影的各边分别为各平行四边行的宽,即水平方向的高,
只要证明这三边等长垂直向量满足向量和,就能保证与面积为长度的垂直向量满足向量和。
作A’F’,AA’‘分别垂直并等长于A’F,A’O, 将A’F’平移到A’'P
过C,作DE垂直于AC,其中CD等于CE,
作CF垂直于BC,其中CB等于CF,
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Eccf5HbQ-1612510802822)(geogebra-export2.png)]

容易证明
∠ A C B = ∠ E C F \angle{ACB}=\angle{ECF} ∠ACB=∠ECF
所以这两个三角形全等:
△ A C B ≅ △ E C F \triangle{ACB} \cong \triangle{ECF} △ACB≅△ECF
所以
∣ A B ⃗ ∣ = ∣ E F ⃗ ∣ = ∣ E C ⃗ + C F ⃗ ∣ = ∣ C D ⃗ + C F ⃗ ∣ |\vec{AB}| = |\vec{EF}| = |\vec{EC} + \vec{CF}| = | \vec{CD} + \vec{CF} | ∣AB∣=∣EF∣=∣EC+CF∣=∣CD+CF∣
即
∣ C D ⃗ + C F ⃗ ∣ = ∣ A B ⃗ ∣ | \vec{CD} + \vec{CF} | = |\vec{AB}| ∣CD+CF∣=∣AB∣
注意:
三棱柱侧面三个平行四边形面积大小是与棱边距离成比例的,而不以底边(即 ∣ a ⃗ ∣ , ∣ b ⃗ ∣ , ∣ a ⃗ + b ⃗ ∣ |\vec{a}|,|\vec{b}|,|\vec{a}+\vec{b}| ∣a∣,∣b∣,∣a+b∣)成比例.
很容易看出 c ⃗ \vec{c} c与 a ⃗ \vec{a} a, b ⃗ \vec{b} b的夹角是不一定相等的,所以对应平行四边形的面自然不与 ∣ a ⃗ ∣ |\vec{a}| ∣a∣, ∣ b ⃗ ∣ |\vec{b}| ∣b∣成比例。
方法2
[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-EcK64Z8N-1612510802824)(geometricCrossProduct2.png)]

A,B,C,D,E在同一平面同。
A B ⃗ + A C ⃗ = A E ⃗ \vec{AB} + \vec{AC} = \vec{AE} AB+AC=AE
下面证明叉乘分配律:
A D ⃗ × ( A B ⃗ + A C ⃗ ) = A D ⃗ × A B ⃗ + A D ⃗ × A C ⃗ \vec{AD} \times ( \vec{AB} + \vec{AC} ) = \vec{AD} \times \vec{AB} + \vec{AD} \times \vec{AC} AD×(AB+AC)=AD×AB+AD×AC
作辅助线
I E ∥ A D IE \parallel AD IE∥AD,
J E ∥ A B JE \parallel AB JE∥AB,
A C ∥ B E AC \parallel BE AC∥BE
I G ⊥ A D IG \perp AD IG⊥AD,
E H ⊥ A D EH \perp AD EH⊥AD,
B F ⊥ A D BF \perp AD BF⊥AD
因为CE = AB
又因为:
∠ E J F = ∠ B A F \angle{EJF} = \angle{BAF} ∠EJF=∠BAF,
∠ E J F = ∠ J E I \angle{EJF} = \angle{JEI} ∠EJF=∠JEI
∠ B A F = ∠ J E I \angle{BAF} = \angle{JEI} ∠BAF=∠JEI
所以直角三角形全等:
△ C I E ≅ △ B F A \triangle{CIE} \cong \triangle{BFA} △CIE≅△BFA
所以
CI = BF
于是
CG + BF = CG + CI = GI = HE
即
S A D C + S A D B = S A D E S_{ADC} + S_{ADB} = S_{ADE} SADC+SADB=SADE
即
A D ⃗ × ( A B ⃗ + A C ⃗ ) = A D ⃗ × A B ⃗ + A D ⃗ × A C ⃗ \vec{AD} \times ( \vec{AB} + \vec{AC} ) = \vec{AD} \times \vec{AB} + \vec{AD} \times \vec{AC} AD×(AB+AC)=AD×AB+AD×AC