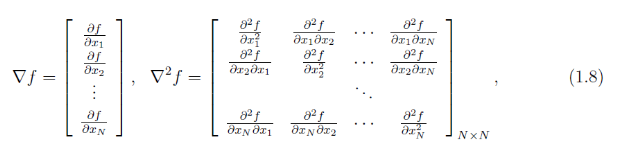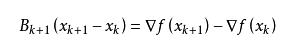简介:牛顿法是用来求解无约束优化问题的,它的基本思想是用迭代点xk处的一阶导数和二阶导数对目标函数进行二次函数近似,然后把二次模型的极小点作为新的迭代点,不断重复这一过程,直至满足精度的近似极小点。
这里有必要讲一下泰勒展开式的几何意义:泰勒公式的几何意义是利用多项式函数来逼近原函数,由于多项式函数可以任意次求导,易于计算,且便于求解极值或者判断函数的性质,因此可以通过泰勒公式获取函数的信息,同时,对于这种近似,必须提供误差分析,来提供近似的可靠性。
基本牛顿法算法的步骤:
步0:确定终止误差e=(0~1),初始点x0,令k=0
步1:计算gk=f(xk).若||gk||<=e,停算,输出xk作为最优解。否则,转步2
步2:计算Gk=^2f(xk),并解出方程组:Gk*dk=-gk,解得dk,其中Gk在xk处要正定
步3:令Xk+1=xk+dk,k=k+1;转步1
这个算法的特点就是他的收敛速度快,缺点就是要求二阶导师,比较麻烦。
还有一个缺点就是它的x0的选取要靠近极小点,否则可能导致算法不收敛,所以x0的选取成为了一个问题,为了改进这个问题,这里用线搜索技术(这里用Armijo线搜索技术)来克服达到大范围收敛的算法,即阻尼牛顿法(与基本的牛顿法相比,它的搜索步长不同,基本的步长是1):
算法步骤:
步0:确定终止误差e=(0~1),初始点x0,=(0~1),
=(0,0.5),令k=0
步1:计算gk=f(xk).若||gk||<=e,停算,输出xk作为最优解。否则,转步2
步2:计算Gk=^2f(xk),并解出方程组:Gk*dk=-gk,解得dk,其中Gk在xk处要正定
步3:求步长k=
^mk,m的值从0开始
若f(xk+ ^m*dk)<=f(xk)+
*
^m*gk'dk
则 mk=m,步长 k=
^mk,若不满足上式,则m=m+1,直到满足上述不等式为止
步4:令Xk+1=xk+ k*dk,k=k+1,转步1
代码实现:
1.阻尼牛顿法
function [x,val,k] =dampnm(fun,gfun,Hess,x0)
%功能:用阻尼牛顿法求解无约束问题minif(x)
%dampnm是阻尼的意思
%输入:fun,gfun,Hess分别是目标函数,梯度,二阶导数,x0是初始点
%输出:x,val分别是近似极小点和近似最优值,k是迭代次数
maxk=100;
rho=0.55;
sigma=0.4;
k=0;
e=1e-5;%精度要求
while(k<maxk)gk=feval(gfun,x0);if(norm(gk)<=e),break;endGk=feval(Hess,x0);dk=-Gk\gk;%右除,解方程Gk*dk=-gkm=0;mk=0;while(m<20)if(feval(fun,x0+rho^m*dk)<feval(fun,x0)+sigma*rho^m*gk'*dk);mk=m;break;endm=m+1;endx0=x0+dk*rho^m;k=k+1;
end
x=x0;
val=feval(fun,x0);
end2.目标函数
function f= fun(x)
%目标函数
f=100*(x(1)^2-x(2))^2+(x(1)-1)^2;
end3.目标函数梯度
function g=gfun(x)
%目标函数的梯度
g=[400*x(1)*(x(1)^2-x(2))+2*(x(1)-1),-200*(x(1)^2-x(2))]';
end
4.目标函数的Hess阵
function f = Hess(x)
%n=length(x);
%f=zero(n,n);
f=[1200*x(1)^2-400*x(2)+2,-400*x(1);-400*x(1), 200];
end
5.主函数
%这个问题的精确值是x=(1,1)',f(x)=0;
clear all
clc
x0=[-1.2 1]';
[x,val,k]=dampnm('fun','gfun','Hess',x0);
disp('迭代次数:k=')
disp(k)
disp(['最优解:x = '])
disp(x)
disp(['此时: f(x) = ',num2str(val)]) 6.结果显示