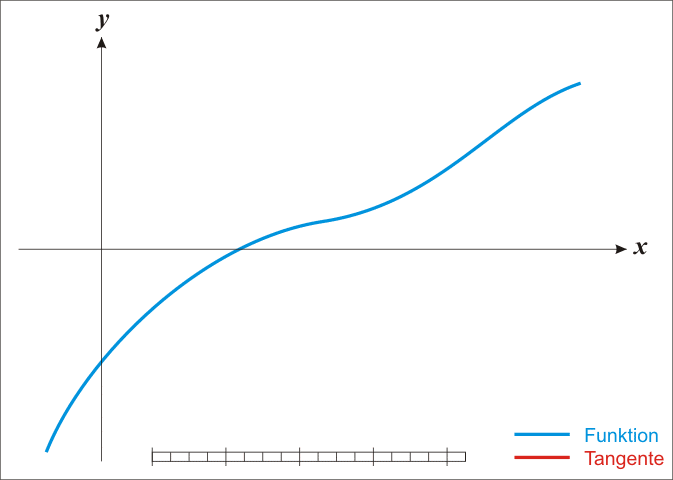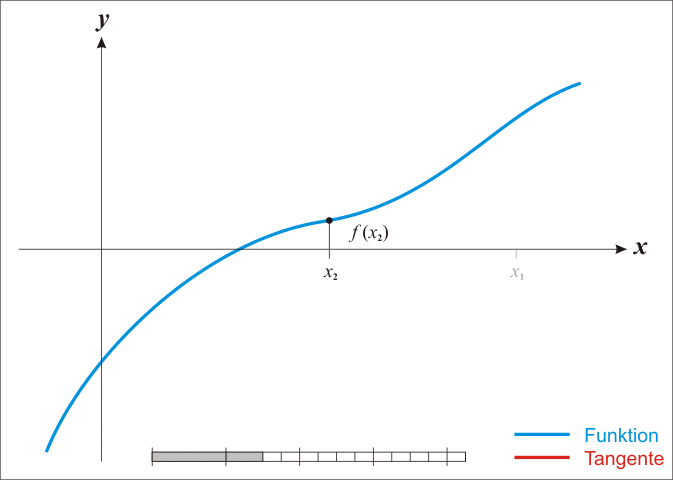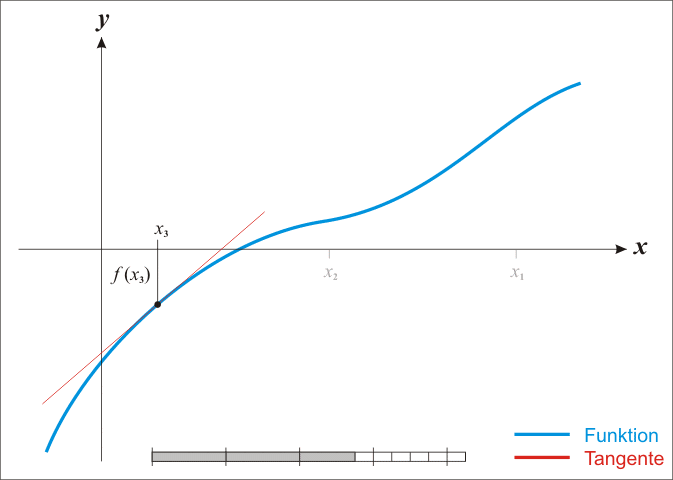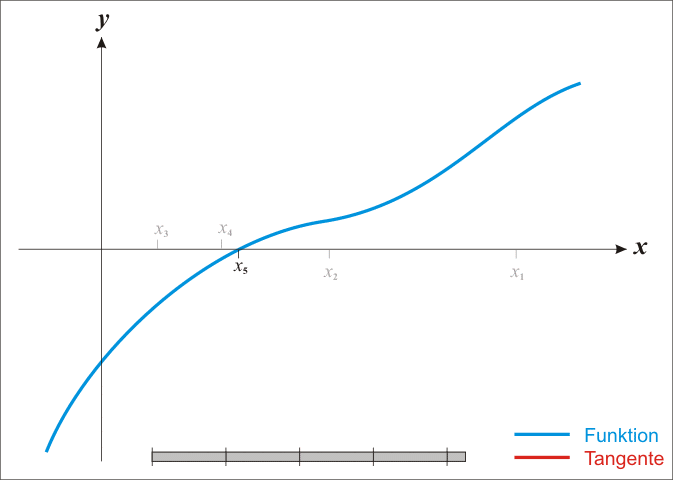
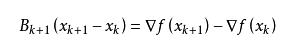牛顿法将目标函数近似为二阶函数，沿着牛顿方向进行优化（包含了Hession矩阵与负梯度信息）。

阻尼牛顿法在更新参数之前进行了一维搜索确定步长，确保沿着下降的方向优化。

拟牛顿法用常数矩阵近似替代Hession矩阵或Hession矩阵的逆矩阵，不用求偏导与求逆，简化运算。

1 牛顿法

1.1 算法流程

梯度下降法利用了负梯度方向进行迭代，算法如下：

                            

1.2 证明过程

对于最优化问题：

                                                                                                                                              (1-1)

对函数进行二阶泰勒展开得到：

                                                           (1-2)

将函数中的看做是变量，令代入(1-2)可以得到：

                                                                          (1-3)

求解最优的x使函数f(x)取得最小值，等价于找到最优的使得取得最小值。令导数=0即可找到极值点，对(1-3)求导数使其=0得到：

                                                                                                                      (1-4)

可以得到：

                                                                                                                        (1-5)

需要逐次迭代可以写为：

                                                                                                                   (1-6)

1.3 几何理解

梯度下降法搜索方向沿着等高线的法向进行搜索，每次迭代优化方向为梯度方向，即当前点所在等高线的法向。但往往等高线很少是正圆形，这种情况下搜索次数会过多。

牛顿法搜索方向为椭圆中心方向，这个方向也叫做牛顿方向，可以看到更新方程的组成分为两部分：毋庸置疑是负梯度信息，包含了该处的曲率（Hession矩阵描述局部曲率）。如下图所示，方向为牛顿方向，为负梯度方向。

                                                             

2 阻尼牛顿法

对于牛顿法，确定了迭代方向之后，迭代步长默认为1，但是这个迭代方向并不一定是朝着函数值下降的方向。可以进行简单判断，对当前迭代的方向与梯度方向进行内积，如果内积为负，则表明迭代方向为下降方向。

当前迭代方向如式（1-6），梯度方向\bigtriangledown f(x_i)。二者乘积为：

                                                                                                               (2-1)

可以看到当且仅当Hession矩阵整定，才满足式（2-1）为负值。

对于牛顿法，当前点的Hession矩阵是正定的，才满足更新方程式下降的，这个限制是非常强的。为了确保每次迭代方向是下降的，提出了阻尼牛顿法，算法如下：

                                          

算法步长计算部分采用一维搜索法。可以看到，阻尼牛顿法相比于牛顿法，在每次参数更新之前，利用一维搜索法计算更新步长，确保优化方向为下降方向。

3 拟牛顿法

3.1 拟牛顿法原理

牛顿法的搜索方向是：

                                                                                                          (3-1)

但是求二阶偏导数并求逆矩阵会带来大量计算，为了避免复杂的运算，拟牛顿法提出了设计矩阵U去近似逆矩阵。但是需要满足一定条件。

任意两点梯度之差公式为：(两点函数值之差等于斜率乘以距离)

                                                                             (3-2)

可以写成：

                                                                          (3-3)

上式为拟牛顿条件。

（1）用于近似的矩阵U一定要正定，因为矩阵U代替了二阶偏导矩阵的功能，由式（2-1）可知需要满足正定。

（2）用于近似的矩阵U一定要满足拟牛顿条件

常用的拟牛顿法有DFP、BFGS，区别在于如何选取替代矩阵U。

3.2 DFP算法

利用矩阵G去替代，并且每次都需要迭代计算可以得到：（为了便于区别，此处即为矩阵G，与3.1中的U同样）

                                                                                                             (3-4)

DFP算法每次采用两个矩阵去近似，即：

                                                                                                        (3-5)

待定。令3-5左右同时乘以可以得到：

                                                                                         （3-6）

为了满足拟牛顿条件（3-3），可以令：

                                                                                     （3-7）

满足3-7的很多，令，可得：

                                                                               

                                                                         

3.3 BFGS算法

GFP算法用于近似拟牛顿条件（3-3），BFGS用于近似拟牛顿条件（3-2）。前者用以替代Hession矩阵的逆，一个用以替代Hession矩阵。

用B矩阵代替：

                                                                          

令，等式两端乘以以可以得到：

                                                              

为了满足拟牛顿条件（3-2）可以令：

                                                                  

满足条件的如下：