牛顿法
求函数的根
牛顿法的最初提出是用来求解方程的根的。我们假设点 x∗ 为函数 f(x) 的根,那么有 f(x∗)=0 。现在我们把函数 f(x) 在点 xk 处一阶泰勒展开有:
f(x)=f(xk)+f′(xk)(x−xk)
那么假设点
xk+1 为该方程的根,则有
f(xk+1)=f(xk)+f′(xk)(xk+1−xk)=0
那么就可以得到
xk+1=xk−f(xk)f′(xk)
这样我们就得到了一个递归方程,我们可以通过迭代的方式不断的让
x 趋近于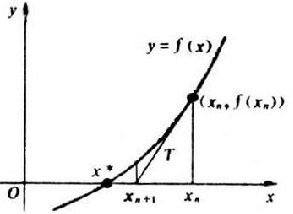
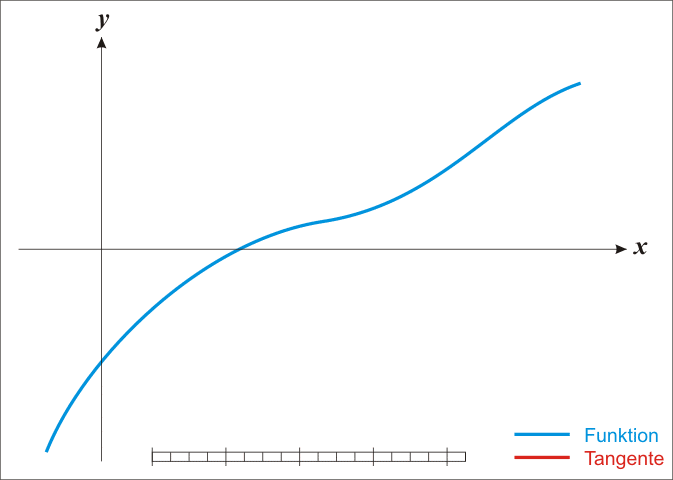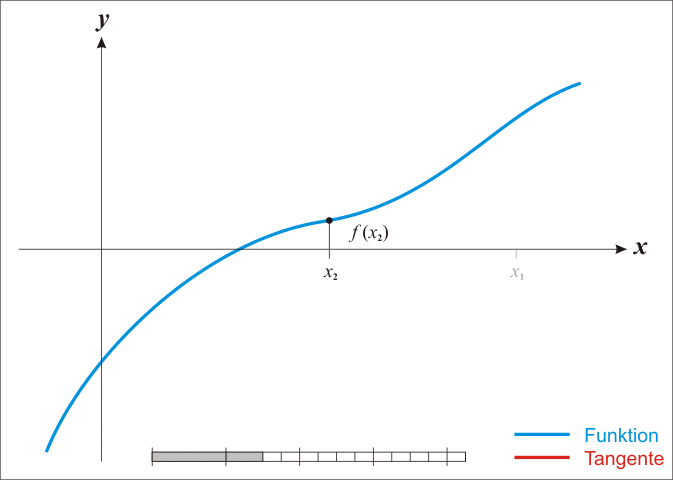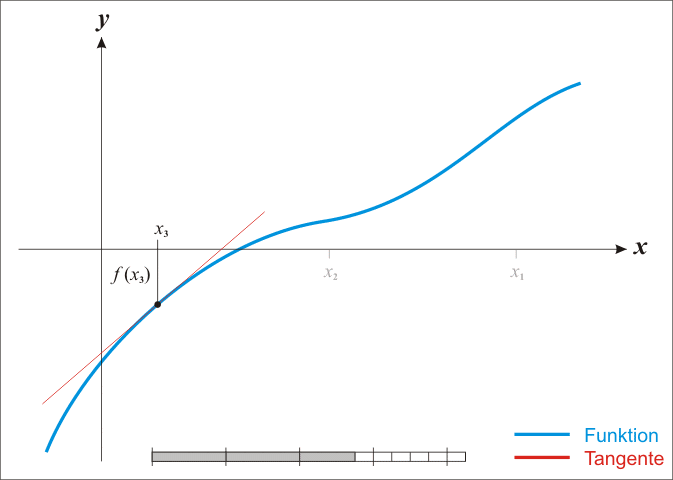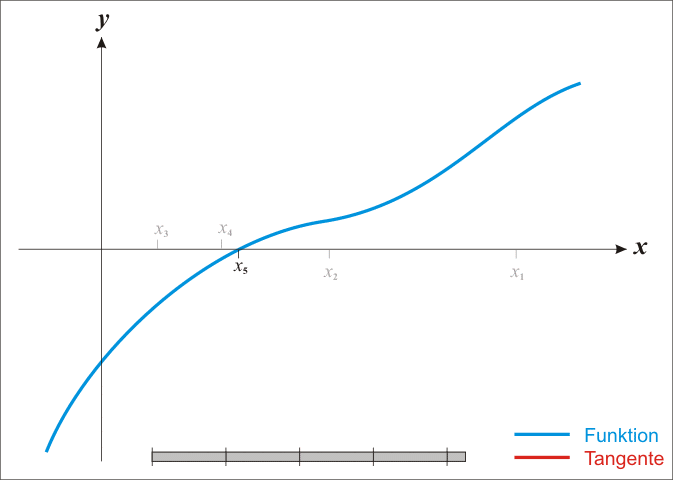
在该图中我们可以看到 xn+1 是要比 xn 更接近于 x∗ ,而 xn+1 利用三角形特征可以知道 xn+1=xn−f(xn)f′(xn) 。其中, f′(xn) 在三角形中表示点 (xn,f(xn)) 处切线的斜率。
最优化
对于最优化问题,其极值点处有一个特性就是在极值点处函数的一阶导数为0。因此我们可以在一阶导数处利用牛顿法通过迭代的方式来求得最优解,即相当于求一阶导数对应函数的根。
首先,我们对函数在 xk 点处进行二阶泰勒展开
f(x)=f(xk)+f′(xk)(x−xk)+12f′′(xk)(x−xk)2⇒
f(x)−f(xk)x−xk=f′(xk)+f′′(xk)(x−xk)
因此,当
x→xk 时,
f′(x)=f′(xk)+f′′(xk)(x−xk) 。这里假设点
xk+1 是一阶导数的根,那么就有
f′(xk+1)=f′(xk)+f′′(xk)(xk+1−xk)=0
依据上式可以得到
xk+1=xk−f′(xk)f′′(xk)
这样我们就得到了一个不断更新
x 迭代求得最优解的方法。这个也很好理解,假设我们上面的第一张图的曲线表示的是函数我们这里讨论的都是在低维度的情形下,那么对于高维函数,其二阶导数就变为了一个海森矩阵,记为 H(x)=[δ2fδxiδxj] ,那么迭代公式就变为了
xk+1=xk−H−1kf′k
我们可以看到,当
Hk 为正定(
H−1k 也为正定)的时候,可以保证牛顿法的搜索方向是向下搜索的。
牛顿法求最优值的步骤如下:
1. 随机选取起始点 x0 ;
2. 计算目标函数 f(x) 在该点 xk 的一阶导数和海森矩阵;
3. 依据迭代公式 xk+1=xk−H−1kf′k 更新 x 值
如果
我们可以看到,当我们的特征特别多的时候,求海森矩阵的逆的运算量是非常大且慢的,这对于在实际应用中是不可忍受的,因此我们想能否用一个矩阵来代替海森矩阵的逆呢,这就是拟牛顿法的基本思路。
拟牛顿法
因为我们要选择一个矩阵来代替海森矩阵的逆,那么我们首先要研究一下海森矩阵需要具有什么样的特征才能保证牛顿法成功的应用。通过上面的描述我们知道
f′(xk+1)=f′(xk)+Hk(xk+1−xk)⇒
H−1K(f′(xk+1)−f′(xk))=xk+1−xk
上式我们称之为拟牛顿条件。
因此,对于我们所选择的替代矩阵 Gk ,需要满足两个条件:
- 拟牛顿条件,即 Gk(f′(xk+1)−f′(xk))=xk+1−xk ;
- 要保证 Gk 为正定矩阵,这是因为只有正定才能保证牛顿法的搜索方向是向下搜索的
假设 yk=f′(xk+1)−f′(xk) , δk=xk+1−xk ,因为每次迭代我们都需要更新替代矩阵 Gk ,下面介绍一种常用的迭代算法DFP(Davidon-Fletcher-Powell)
DFP算法
DFP算法中选择 Gk+1 的方法是在每一步迭代中在矩阵 Gk 中加两项附加项构成 Gk+1 ,即
Gk+1=Gk+Pk+Qk
我们有
Gk+1yk=Gkyk+Pkyk+Qkyk
,我们可以令
Pkyk=δk,Qkyk=−Gkyk ,这样就可以得到
Gk 的迭代公式