1 最优化方法的结构

最优化问题的一般形式为：

$min f(x)$
$s.t. x\in X$

其中 $x$ 为决策变量， $f(x)$ 是目标函数， $X$ 为约束集或可行域。特别地，如果 $X=R^n$ ，则最优化问题成为无约束最优化问题。

最优化方法通常采用迭代法求它的最优解，其基本思想是：给定一个初始点 $x_0$ ，按照某一迭代规则产品一个点列{ $x_n$ }，使得当{ $x_n$ }是有穷点列时，其最后一个点是最优化模型问题的最优解。迭代规则由迭代公式决定，迭代公式的基本表示形式如下：

$x_{k+1}=x_k+\alpha _kd_k$

式中， $\alpha _k$ 为步长因子， $d_k$ 为搜索方向。在最优化算法中，搜索方向 $d_k$ 是 $f$ 在 $x_k$ 点处的下降方向，即：

$f(x_k+\alpha _kd_k)<f(x_k)$

最优化方法的基本结构如下：

给定初始点 $x_0$ ；
确定搜索方向 $d_k$ ，即按照一定规则，构造 $f$ 在 $x_k$ 点处的下降方向作为搜索方向；
确定步长因子 $\alpha _k$ ，使目标函数有某种意义的下降；
令 $x_{k+1}=x_k+\alpha _kd_k$ ，若 $x_{k+1}$ 满足某种终止条件，则停止迭代，得到近似最优解 $x_{k+1}$ .否则，重复以上步骤。

2 常用最优化方法对比分析

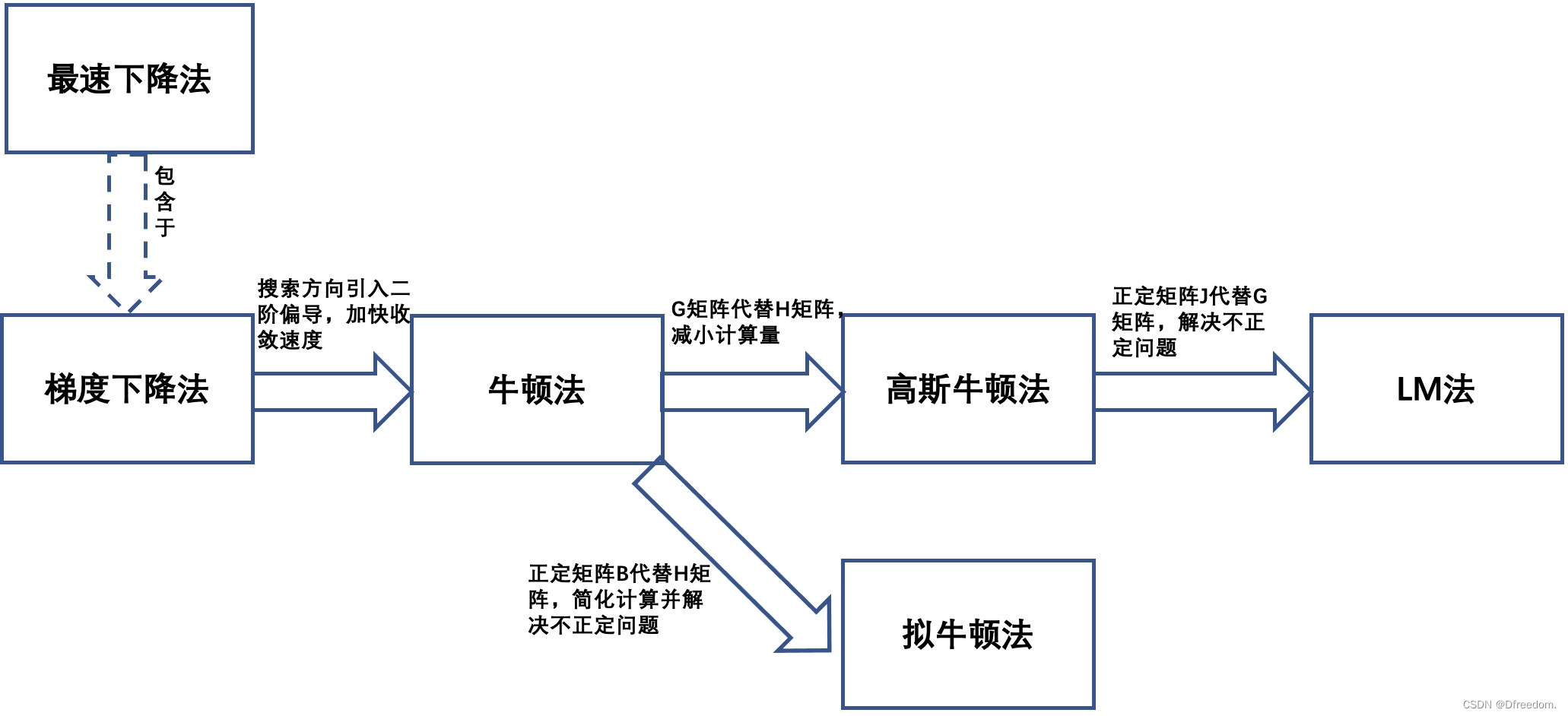
从迭代公式可知，最优化方法求解时的关键就是构造搜索方向 $d_k$ 和步长因子 $\alpha _k$ 。不同的搜索方向和不同的步长因子构成了不同的方法，常见的最优化方法有梯度下降法、最速下降法、牛顿法、高斯牛顿法、LM法、拟牛顿法，对应的迭代公式总结如下表：

	迭代公式
梯度下降法	$x^{k+1}=x^k- \alpha \triangledown f(x^k)$
最速下降法	$x^{k+1}=x^k- \alpha_k \triangledown f(x^k)$
牛顿法	$x^{k+1}=x^k- \alpha_kH(x^k)^{-1} \triangledown f(x^k)$
高斯牛顿法	$x^{k+1}=x^k- \alpha_kG(x^k)^{-1} \triangledown f(x^k)$
LM法	$x^{k+1}=x^k- \alpha_kJ(x^k)^{-1} \triangledown f(x^k)$
拟牛顿法	$x^{k+1}=x^k- \alpha_kB(x^k)^{-1} \triangledown f(x^k)$

对比分析：

	梯度下降法	最速下降法	牛顿法	高斯牛顿法	LM法	拟牛顿法
步长因子	$\alpha$	$\alpha _k$	$\alpha _k$	$\alpha _k$	$\alpha _k$	$\alpha _k$
搜索方向	$-\triangledown f(x^k)$	$-\triangledown f(x^k)$	$-H(x^k)^{-1}\triangledown f(x^k)$	$-G(x^k)^{-1}\triangledown f(x^k)$	$-J(x^k)^{-1}\triangledown f(x^k)$	$-B(x^k)^{-1}\triangledown f(x^k)$
参数说明	① 步长因子 $\alpha$ 为一个固定值，工程师预先设定；② 搜索方向为梯度方向 $\triangledown f(x^k)$ 的反方向	步长因子是一个变化的常数 $\alpha _k$ ，每一次迭代需要重新计算。通过一位搜索算法得到	H为二阶偏导矩阵，即海塞矩阵	G矩阵用来近似替代H矩阵， $G=\triangledown f\triangledown f^T$	J矩阵替代G矩阵， $J=G+uI$ ，u为常数， $I$ 为单位矩阵	B矩阵用来近似替代H矩阵，B矩阵的形式有多种
目的	求解最优化问题的基本方法	梯度下降法的一种具体的实现方式	提高收敛速度	减小计算量	解决G矩阵不正定的问题	减小计算量以及H矩阵不正定的问题

几种算法之间的关系总结如下：

最速下降法是梯度下降法的一种具体实现方式。梯度下降法的步长因子是固定值，最速下降法的步长因子是一个变化的常数 $\alpha _k$ ，即由一位搜索得到步长因子 $\alpha _k$ ，使得

$f(x_k+\alpha _kd_k)=minf(x_k+\alpha d_k),\alpha >0$

牛顿法可以看成相对于梯度下降法的改进，提高了收敛速度。梯度下降法/最速下降法在确定搜索方向的时候，只用到了一阶导数，因此它的收敛速度是一阶收敛，收敛速度较慢。而牛顿法用到了二阶偏导，它的收敛速度是二阶收敛，收敛速度比梯度下降法快。
高斯牛顿法是相对于牛顿法改进，简化了计算。牛顿法中的H矩阵需要计算目标函数的二阶偏导，计算量巨大，高斯牛顿法采用G矩阵替代H矩阵，大大减小了计算量。
LM法是相对于高斯牛顿法的改进，解决G矩阵正定问题。高斯-牛顿法的逼近步长由矩阵G的逆矩阵决定，如果矩阵G非正定，那么其逆矩阵不一定存在，即使存在逆矩阵，也会导致逼近方向出现偏差，严重影响优化方向。LM法正是为了解决矩阵G的正定问题而提出的，其将矩阵G加上单位矩阵I的倍数来解决正定问题。
LM法相当于最速下降法和高斯牛顿法的结合体。当u很小时，矩阵J接近矩阵G，其相当于高斯-牛顿法，此时迭代收敛速度快，当u很大时，其相当于梯度下降法，此时迭代收敛速度慢。因此LM算法即具有高斯-牛顿法收敛速度快、不容易陷入局部极值的优点，也具有梯度下降法稳定逼近最优解的特点。
拟牛顿法是相对于牛顿法的改进。牛顿法虽然收敛速度快，但是需要计算海塞矩阵的逆矩阵 $H^{-1}$ ，而且有时目标函数的海塞矩阵无法保持正定，从而使得牛顿法失效。为了克服这两个问题，人们提出了拟牛顿法。这个方法的基本思想是：不用二阶偏导数而构造出可以近似海塞矩阵（或海塞矩阵的逆）的正定对称阵。不同的构造方法就产生了不同的拟牛顿法，常用的拟牛顿算法有：DFP算法、BFGS算法、L-BFGS算法。严格意义上讲高斯牛顿法和LM法都属于拟牛顿法。