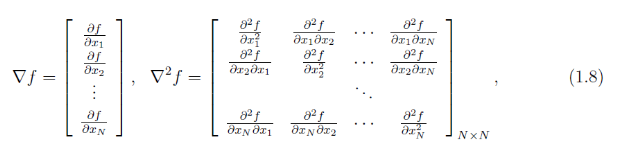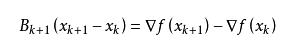拟牛顿法求解非线性方程
- 开始
- 牛顿迭代法
- 拟牛顿法
- 数值计算比较
开始
最近博主在研究非线性方程组的解法,有很多种方法,这里主要对牛顿迭代与拟牛顿迭代进行阐述与对比,由于水平有限,若有错误还请见谅并指出。
牛顿迭代法
相信许多学过《数值分析》课程的朋友都对大名鼎鼎的牛顿迭代不会陌生,但是对于方程组的求解还是有些许的区别,这里的区别不是理论上的区别,而是在计算过程中是矩阵运算,而不是一个数的运算。下面言归正传。
牛顿迭代利用了当前迭代点的位置信息和切线信息。
0 = F ( x ∗ ) ≈ F ( x k ) + F ′ ( x k ) ( x ∗ − x k ) 0=F(x^*)\approx F(x^k)+F'(x^k)(x^*-x^k) 0=F(x∗)≈F(xk)+F′(xk)(x∗−xk)当然此时 F ′ ( x k ) F'(x^k) F′(xk)就是Jacobian矩阵带入 x k x^k xk的值。
好了,根据上式,我们可以轻易退出 x k x^k xk的迭代公式:
x k + 1 = x k − ( F ′ ( x k ) ) − 1 ( F ( x k ) ) x^{k+1}=x^k-(F'(x^k))^{-1}(F(x^k)) xk+1=xk−(F′(xk))−1(F(xk))每一次迭代都是当前点的切线与 F ( x k + 1 ) = 0 F(x^{k+1})=0 F(xk+1)=0相交进而求得下一次迭代点。很简单把,利用上述公式可以很快求出不动点 x ∗ x^* x∗。牛顿迭代是二阶收敛,速度还是很快的。但是牛顿迭代也有一些限定条件,即初始点要充分靠近 x ∗ x^* x∗。但很多问题中上述条件是不好满足的。
拟牛顿法
众所周知,对于矩阵逆的求解,运算量是比较大的,更别说每次迭代都要计算一次。所以拟牛顿法出现了。拟牛顿法既保留了牛顿法收敛速度快的优点,又克服了需要每次计算Jacobian矩阵的逆这一问题。它的主要思想的利用割线而非切线的信息。
先摆出后面要用到的拟牛顿方程
A k + 1 ( x k + 1 − x k ) = F ( x k + 1 ) − F ( x k ) A_{k+1}(x^{k+1}-x^{k})=F(x^{k+1})-F(x^k) Ak+1(xk+1−xk)=F(xk+1)−F(xk)是不是很熟悉,这不就是以前学过的割线方程吗, A k + 1 A_{k+1} Ak+1可以认为是经过两点连线的斜率。但是由拟牛顿方程并不能确定矩阵 A k + 1 A_{k+1} Ak+1,因此,天才的数学家又给它加了一个修正方程
A k + 1 = A k + Δ A k A_{k+1}=A_k+\Delta A_k Ak+1=Ak+ΔAk没经过一次迭代, A k A_k Ak都要根据这个方程进行更新。 Δ A k \Delta A_k ΔAk的不同造就了不同的拟牛顿方法。 A k A_k Ak增量矩阵的秩为1时称为秩1方法, A k A_k Ak秩为2时称为秩2方法,应用广泛的DFP和BFGS均为秩2方法。
- Broyden秩1方法
Δ A k = u k v k T \Delta A_k=u_kv_k^T ΔAk=ukvkT,其中 u k u_k uk和 v k T v_k^T vkT均为向量。
令
s k = x k + 1 − x k , y k = F ( x k + 1 ) − F ( x k ) s_k =x^{k+1}-x^{k}, y_k=F(x^{k+1})-F(x^{k}) sk=xk+1−xk,yk=F(xk+1)−F(xk)令 v k = u k v_k=u_k vk=uk可得
Δ A k = 1 ∣ ∣ s k ∣ ∣ 2 ( y k − A k ∗ s k ) s k T \Delta A_k=\frac{1}{||s_k||^2}(y_k-A_k*s_k)s_k^T ΔAk=∣∣sk∣∣21(yk−Ak∗sk)skT于是得到迭代步骤为: x k + 1 = x k − A k − 1 F ( x k ) s k = x k + 1 − x k , y k = F ( x k + 1 ) − F ( x k ) A k + 1 = A k + 1 ∣ ∣ s k ∣ ∣ 2 ( y k − A k ∗ s k ) s k T x^{k+1}=x^k-A_k^{-1}F(x^k)\\ s_k =x^{k+1}-x^{k}, y_k=F(x^{k+1})-F(x^{k})\\ A_{k+1}=A_k+\frac{1}{||s_k||^2}(y_k-A_k*s_k)s_k^T xk+1=xk−Ak−1F(xk)sk=xk+1−xk,yk=F(xk+1)−F(xk)Ak+1=Ak+∣∣sk∣∣21(yk−Ak∗sk)skT - 逆Broyden秩1方法
为了避免求逆,可以应用逆Broyden秩1方法
x k + 1 = x k − B k F ( x k ) s k = x k + 1 − x k , y k = F ( x k + 1 ) − F ( x k ) B k + 1 = B k + 1 s k T B k y k ( s k − B k y k ) s k T B k x^{k+1}=x^k-B_kF(x^k)\\ s_k =x^{k+1}-x^{k}, y_k=F(x^{k+1})-F(x^{k})\\ B_{k+1}=B_k+\frac{1}{s_k^TB_ky_k}(s_k-B_ky_k)s_k^TB_k xk+1=xk−BkF(xk)sk=xk+1−xk,yk=F(xk+1)−F(xk)Bk+1=Bk+skTBkyk1(sk−Bkyk)skTBk - DFP
这里只给出矫正公式:
B k + 1 = B k + δ k δ k T δ k T δ k − B k y k y k T B k y k T B k y k B_{k+1}=B_k+\frac{\delta _k\delta _k^T}{\delta _k^T\delta _k}-\frac{B_ky_ky_k^TB_k}{y_k^TB_kyk} Bk+1=Bk+δkTδkδkδkT−ykTBkykBkykykTBk - BFGS
同样只给出矫正公式
B k + 1 = B k + y k y k T y k T δ k − B k δ k δ k T B k δ k T B k δ k B_{k+1}=B_k+\frac{y_ky _k^T}{y_k^T\delta _k}-\frac{B_k\delta _k\delta _k^TB_k}{\delta _k^TB_k\delta _k} Bk+1=Bk+ykTδkykykT−δkTBkδkBkδkδkTBk
BFGS被普遍认为是拟牛顿法中最好的一个,
数值计算比较
求解 F ( x ) = 0 F(x)=0 F(x)=0,其中
F ( x ) = [ 3 x 1 − cos ( x 2 x 3 ) − 1 2 x 1 2 − 81 ( x 2 + 0.1 ) 2 + s i n ( x 3 ) + 1.06 e x p ( − x 1 x 2 ) + 20 x 3 + 1 3 ( 10 ∗ π − 3 ) ] F(x)=\begin{bmatrix} 3x_1-\cos(x_2x_3)-\frac{1}{2}\\x_1^2-81(x_2+0.1)^2+sin(x_3)+1.06\\exp(-x_1x_2)+20x_3+\frac{1}{3}(10*\pi-3)\end{bmatrix} F(x)=⎣⎡3x1−cos(x2x3)−21x12−81(x2+0.1)2+sin(x3)+1.06exp(−x1x2)+20x3+31(10∗π−3)⎦⎤
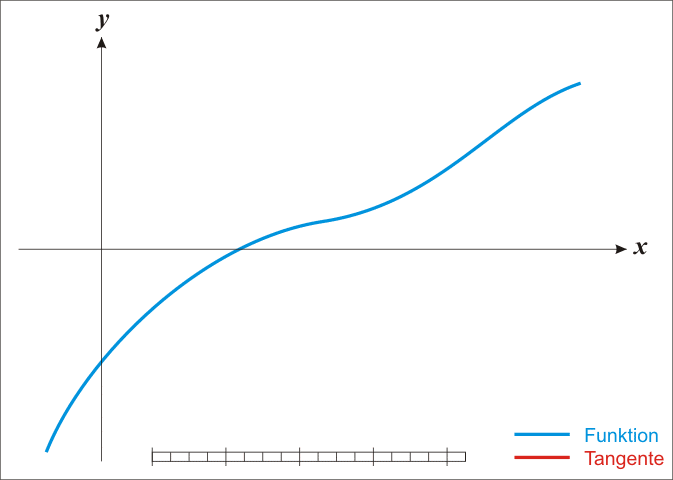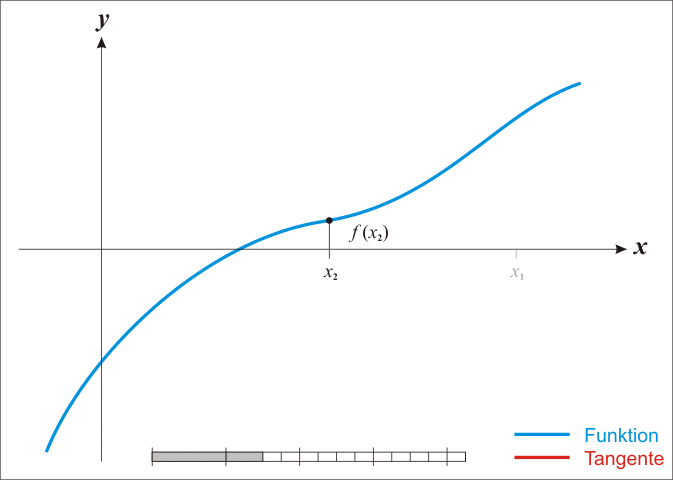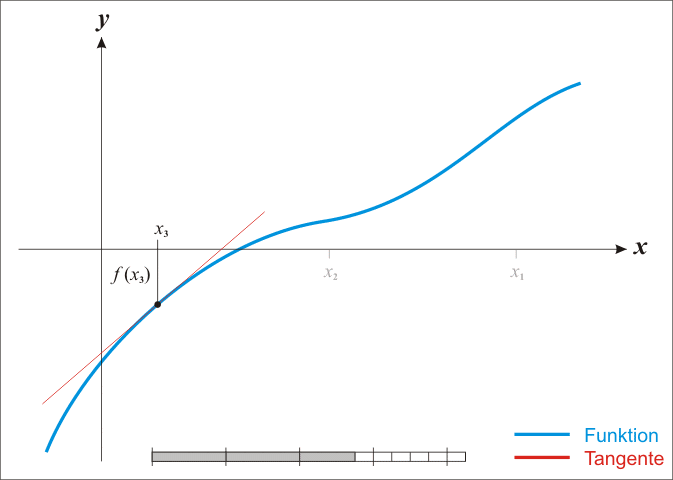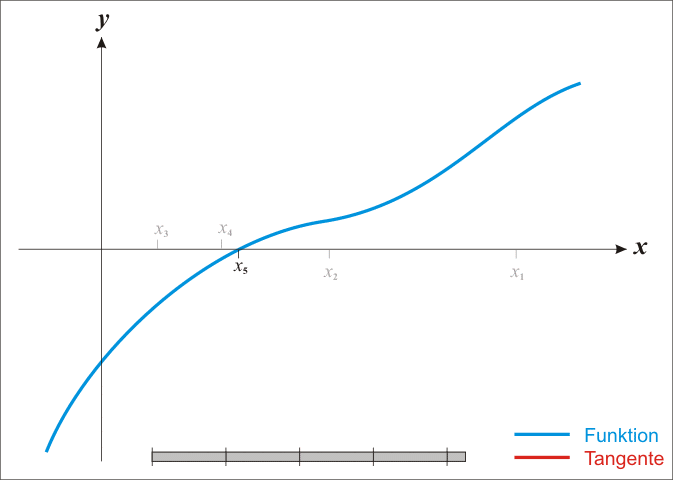
设置初始计算点为 ( 0.1 , 0.1 , 0.1 ) T (0.1,0.1,0.1)^T (0.1,0.1,0.1)T,利用牛顿迭代只需7次迭代就可达到计算精度,第一张图显示了牛顿迭代计算过程。而利用BFGS计算,需要利用线搜索(armijo搜索)寻找合适的步长,步长的选取对算法的收敛性有明显影响,要小心选取参数进行计算,第二张图显示了BFGS计算过程,同样用了7次。但若如果在计算步长时参数设置不合适,那收敛过程可能非常缓慢。