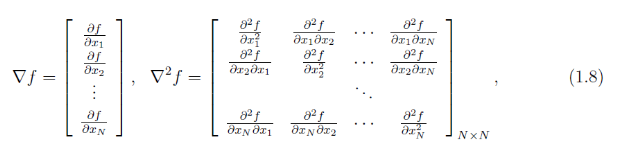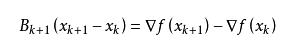转自:ACdreamer

今天，我来讲一种在机器学习中常用到的优化算法，叫做BFGS算法。BFGS算法被认为是数值效果最好的拟牛顿

法，并且具有全局收敛性和超线性收敛速度。那么接下来将会详细讲解。

 

Contents

 

   1. 什么是拟牛顿法

   2. 拟牛顿法原理

   3. DFP算法原理

   4. BFGS算法原理

   5. BFGS算法的实现

 

 

1. 什么是拟牛顿法

 

   前面Logisitc回归讲解中，我介绍了牛顿法。牛顿法的特点是：收敛速度快，迭代次数少，但是当Hessian

   矩阵很稠密时，每次迭代的计算量很大。随着数据规模的增大，那么Hessian矩阵会越大，需要的存储空间会

    增多，计算量也会增大，有时候大到不可计算，所以针对海量数据的计算，牛顿法不再适用。

 

   拟牛顿法是在牛顿法的基础上引入了Hessian矩阵的近似矩阵，避免每次迭代都计算Hessian矩阵的逆，它

   的收敛速度介于梯度下降法和牛顿法之间。拟牛顿法跟牛顿法一样，也是不能处理太大规模的数据，因为计算

   量和存储空间会开销很多。拟牛顿法虽然每次迭代不像牛顿法那样保证是最优化的方向，但是近似矩阵始终是

   正定的，因此算法始终是朝着最优化的方向在搜索。

 

 

2. 拟牛顿法原理

 

   拟牛顿法的基本思想是在牛顿法中用Hessian矩阵的某个近似矩阵来代替它。在高数中，学过泰勒公式，如下

 

       

 

   关于泰勒展开的更多内容，可以参考这里：泰勒公式介绍，泰勒公式应用。泰勒公式是用一个近似的多项式

   来代替原来复杂的函数表达式。对于拟牛顿法来说，构造二次模型。如下

 

   

 

   忽略高阶无穷小部分，进行求导得到

 

       

 

   令，那么得到

 

       

 

   牛顿迭代中，要求Hessian矩阵的逆，计算量增大，而拟牛顿法是用Hessian矩阵的逆矩阵来代替Hessian

   矩阵。即如下迭代式

 

       

 

   这个方程就是拟牛顿方程，这就是拟牛顿的核心公式啊。所以最关键的问题是如何得到每一步的。关

   于这个问题，又有很多种方法来迭代计算，接下来主要介绍DFP算法和BFGS算法。

 

 

3. DFP算法原理

 

   在上面的拟牛顿法原理介绍中，已经得到拟牛顿方程。现在来介绍一种算法，叫做DFP算法，它是Davidon、

   Fletcher、Powell三位牛人名字的首字母缩写。在DFP算法中，假设有如下迭代

 

       

 

   其中和均为实数，和均为维向量，那么带入上述的拟牛顿方程中，有如下推导

 

       

 

   那么进一步有

   

 

 

   接下来，我们重新记一下符号，设

 

   

 

   那么得到

 

   

 

   现在只要我们求出了，，，，那么问题也就解决了。那么为了更容易看出结论，继续作如下变换

 

   

 

   那么只需要如下几个条件成立就可以了

 

   

 

   带入原式最终得到

 

   

 

   由于虽然是有矩阵相乘，但是实际上是向量相乘，然后又矩阵相加，所以时间复杂度为，比起普通

   牛顿迭代矩阵求逆来说，时间复杂度大大降低，这就是DFP算法的原理。

 

 

4. BFGS算法原理

 

   上面的DFP算法中，已经很好地解决了问题，接下来，继续学习BFGS算法。它是Broyden，Fletcher，

   Goldfarb，Shanno四位牛人发明出来到现在的40多年时间里，它仍然被认为是最好的拟牛顿算法。假设

   迭代如下

 

       

 

   这样最终得到迭代式如下

 

       

 

   这就是BFGS算法的原理。

 

 

 

5. BFGS算法的实现

 

   BFGS算法的C++实现参考这里。在Python中，有一个优化算法工具，叫做scipy。scipy中的optimize子

   包中提供了常用的最优化算法函数实现。我们可以直接调用这些函数完成我们的优化问题。optimize中函数

   最典型的特点就是能够从函数名称上看出是使用了什么算法，可以参考这里。比如BFGS算法的用法如下

 

    

 

   运行结果如下