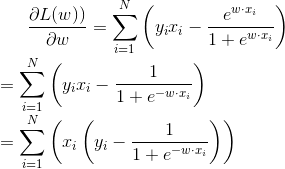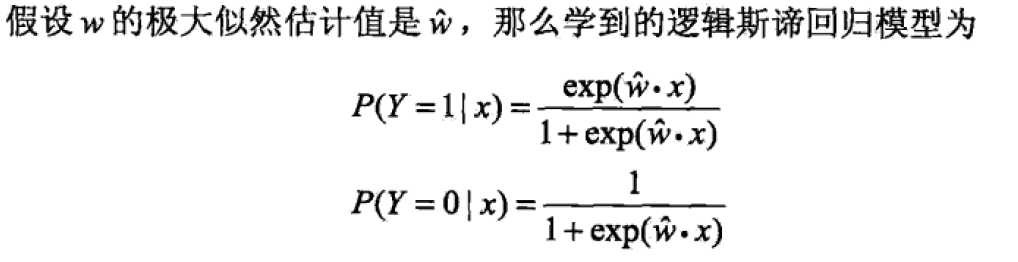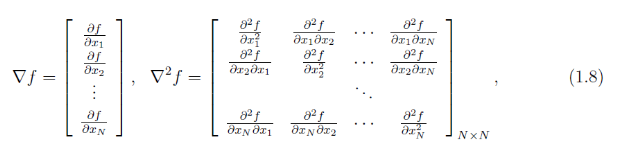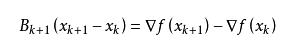介绍

在向量微积分中，标量场的梯度是一个向量场。标量场中某一点上的梯度指向标量场增长最快的方向，梯度的长度是这个最大的变化率。更严格的说，从欧几里得空间Rn到R的函数的梯度是在Rn某一点最佳的线性近似。

在判别式模型中，我们往往需要学习参数，从而使得我们的模型f(x)可以逼近实际的y。如果学习参数，则通常会用到梯度下降、牛顿、拟牛顿学习算法。

参考自网络资源

1.梯度下降

1.1 为何使用梯度作为下降方向？

梯度实际上是函数值变化最快的方向。

比如说，你站在一个山上，梯度所指示的方向是高度变化最快的方向。你沿着这个方向走，能最快的改变（增加或是减小）你所在位置的高度，但是如果你乱走，可能走半天所在位置高度也没有变化多少。也就是说，如果你一直沿着梯度走，你就能最快的到达山的某个顶峰或低谷（偶尔会到鞍点，不过这几乎不可能）。

所以实际上，梯度下降法是用来数值搜索局部极小值或极大值的，它是实际应用中一种非常高效，高速且可靠的方法。

1.2 以逻辑斯蒂回归（LR）为例

1. 模型参数估计
   
2. 梯度下降学习参数
   
3. 最终模型
   

1.3 具体学习过程(python代码示例)

梯度下降是最小化风险函数、损失函数的一种常用方法，随机梯度下降和批量梯度下降是两种迭代求解思路。

根据batch_size的不同，可以有大概一下几种形式。

（1）梯度下降伪代码

• 每个回归参数初始化为1
• 重复R次
  
  • 计算整个数据集的梯度
  • 使用alpha × gradient更新回归系数的向量
  • 返回回归系数

示例代码：

def gradAscent(dataMatIn, classLabels):dataMatrix = mat(dataMatIn)             #convert to NumPy matrixlabelMat = mat(classLabels).transpose() #convert to NumPy matrixm,n = shape(dataMatrix)alpha = 0.001maxCycles = 500weights = ones((n,1))for k in range(maxCycles):              #heavy on matrix operationsh = sigmoid(dataMatrix*weights)     #matrix multerror = (labelMat - h)              #vector subtractionweights = weights + alpha * dataMatrix.transpose()* error #matrix multreturn weights

（2）随机梯度下降伪代码：

• 每个回归参数初始化为1
• 重复R次
  
  • 计算每个样本的梯度
  • 使用alpha × gradient更新回归系数的向量
  • 返回回归系数

示例代码：

细心的读者可以看到，其中alpha是变化的，这样可以在一定程度上避免局部最优解。

def stocGradAscent1(dataMatrix, classLabels, numIter=150):m,n = shape(dataMatrix)weights = ones(n)   #initialize to all onesfor j in range(numIter):dataIndex = range(m)for i in range(m):alpha = 4/(1.0+j+i)+0.0001    #apha decreases with iteration, does not randIndex = int(random.uniform(0,len(dataIndex)))#go to 0 because of the constanth = sigmoid(sum(dataMatrix[randIndex]*weights))error = classLabels[randIndex] - hweights = weights + alpha * error * dataMatrix[randIndex]del(dataIndex[randIndex])return weights

（3）自定义batch_size,算法流程与上面基本差不错，累计误差更新参数。梯度下降，就是batch_size = 全部样本量，随机梯度下降就是batch_size = 1。

2.牛顿法

2.1 基本介绍

在最优化的问题中，线性最优化至少可以使用单纯行法求解，但对于非线性优化问题，牛顿法提供了一种求解的办法。假设任务是优化一个目标函数f，求函数f的极大极小问题，可以转化为求解函数f的导数f’=0的问题，这样求可以把优化问题看成方程求解问题（f’=0）。

为了求解f’=0的根，把f（x）的泰勒展开，展开到2阶形式：

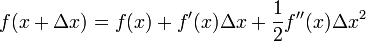
这个式子是成立的，当且仅当 Δx 无线趋近于0。此时上式等价与：

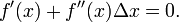
求解：

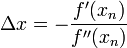
得出迭代公式：

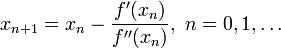
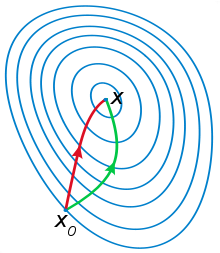
一般认为牛顿法可以利用到曲线本身的信息，比梯度下降法更容易收敛（迭代更少次数），如下图是一个最小化一个目标方程的例子，红色曲线是利用牛顿法迭代求解，绿色曲线是利用梯度下降法求解。

二维情形，图片来源自网络

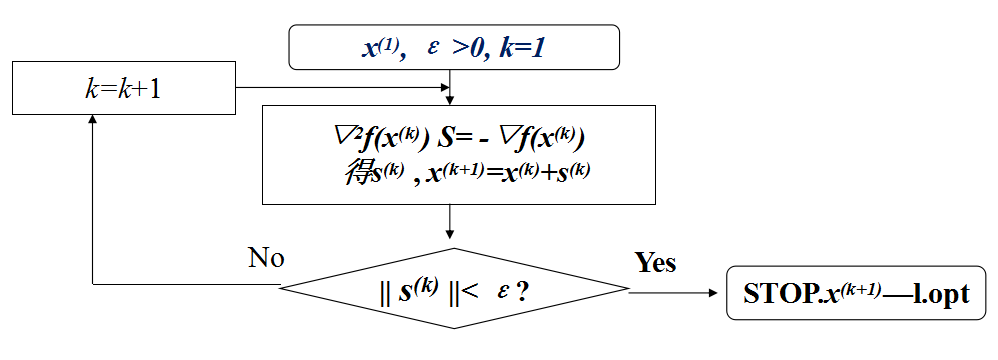
2.2 算法流程

2.3 特性

1. 牛顿法收敛速度为二阶，对于正定二次函数一步迭代即达最优解。
2. 牛顿法是局部收敛的，当初始点选择不当时，往往导致不收敛
3. 牛顿法不是下降算法，当二阶海塞矩阵非正定时，不能保证产生方向是下降方向。
4. 二阶海塞矩阵必须可逆，否则算法进行困难。
5. 对函数要求苛刻（二阶连续可微，海塞矩阵可逆），而且运算量大。

2.4 牛顿法的改进

3.拟牛顿法

3.1 特征

1. 只需用到函数的一阶梯度；（Newton法用到二阶Hesse阵）
2. 下降算法，故全局收敛；
3. 不需求矩阵逆；（计算量小）
4. 一般可达到超线性收敛；（速度快）
5. 有二次终结性。

3.2 DFP法

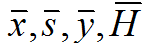
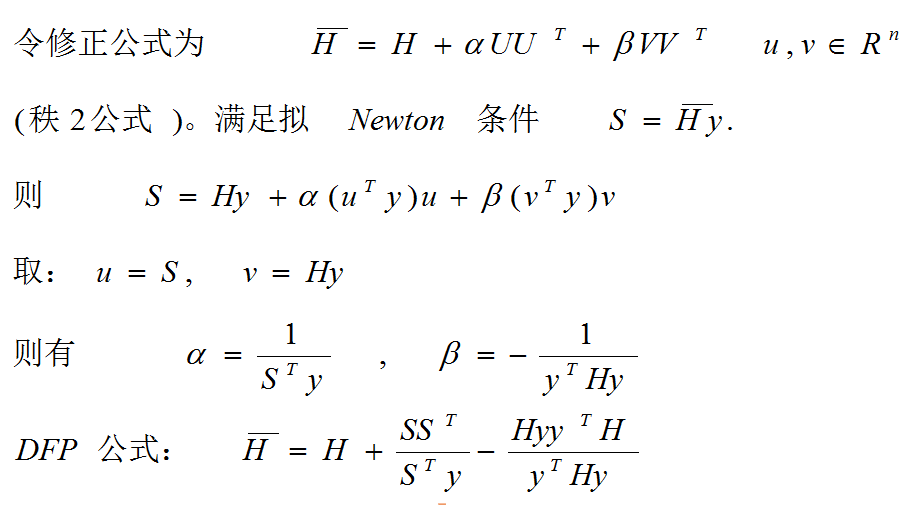
x, s, y, H 表示第k 步的量，等表示第k+1步的量。

3.3 BFGS法

若把前面的推导，平行地用在y=Bs公式上，可得到

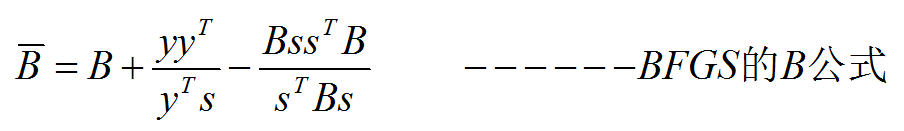
用此公式求方向时，需用到矩阵求逆或解方程

由于每次只有秩2的变换，这里的计算量仍可以降下来。为了得到H-公式，可对上面求逆（推导得）：

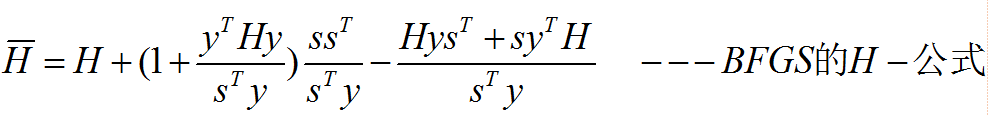
BFGS法有拟牛顿法的全部优点，并且在一定条件下可以证明在BFGS法中使用不精确一维搜索有全局收敛性。

参考文献
（1）《统计学习方法》
（2）《机器学习实战》
（3）《运筹学与最优化方法》