1.什么是正交性?
“正交性”是从几何中借来的术语。如果两条直线相交成直角,他们就是正交的。在空间向量中,两个向量的标量积为零即两个向量正交。
如果两个函数满足
,则称这两个函数正交。
2.什么是三角函数正交信号集?
三角函数正交信号集:,其中
。
当n=1 , m=1时,信号集里的信号称之为基频信号;其他信号称之为n次谐波(m次谐波)。
3.什么是三角函数正交性?
三角函数正交性是指三角函数正交信号集里面的任意不同信号或者不同阶次的信号在基频信号周期内乘积的积分值为0;相同信号在基频信号周期内乘积的积分值不为0。这种特性利用在单边带信号调制,OFDM调制等。
假设基频信号的周期为,则正交信号集里面的信号正交性计算存在三种情况:
1.
2.
3.
由三角函数的积化和差公式可以将上面三个公式推导出如下结果:
1. ,由公式可知不论n,m取何值积分结果都是0;
2. ,由公式可知n=m时,积分结果是T/2;当n≠m是,在T时间内积分结果都是0;
3. ,由公式可知n=m时,积分结果是T/2;当n≠m是,在T时间内积分结果都是0;
4.Matlab分析三角函数正交性
针对上面的三种情况分别进行仿真,仿真代码如下:
clear all
close all
clc
% Orthogonal of trig function
f = 1000;%the base frequence
fs = 1e6;%the sampling frequence
% Generate the signals
Td = 1000;%time of duration
for k = 1:Td % f = 1000,T = 1/f = 1000/fsReal_Signal_1(k,1) = cos(2*pi*f*k/fs);% the 1st degree cos frequenceReal_Signal_2(k,1) = cos(2*pi*2*f*k/fs);% the 2st degree cos frequenceReal_Signal_3(k,1) = cos(2*pi*3*f*k/fs);% the 3st degree cos frequenceImag_Signal_1(k,1) = sin(2*pi*f*k/fs);% the 1st degree sin frequenceImag_Signal_2(k,1) = sin(2*pi*2*f*k/fs);% the 2nd degree sin frequenceImag_Signal_3(k,1) = sin(2*pi*3*f*k/fs);% the 3rd degree sin frequence
end
% Integral cos*sin in T
% Integral cos*cos in T
% Integral sin*sin in T
% The integral results
Int_Result0 = sum(Real_Signal_1.*Imag_Signal_1);
Int_Result1 = sum(Real_Signal_1.*Imag_Signal_2);
Int_Result2 = sum(Real_Signal_1.*Imag_Signal_3);
Int_Result3 = sum(Real_Signal_1.*Real_Signal_1);
Int_Result4 = sum(Real_Signal_1.*Real_Signal_2);
Int_Result5 = sum(Real_Signal_1.*Real_Signal_3);
Int_Result6 = sum(Imag_Signal_1.*Imag_Signal_1);
Int_Result7 = sum(Imag_Signal_1.*Imag_Signal_2);
Int_Result8 = sum(Imag_Signal_1.*Imag_Signal_3);
% Plot
t = 1/1000:1/1000:1;
figure
plot(t,Real_Signal_1,'LineWidth',3,'color','k');
hold on
plot(t,Real_Signal_2,'LineWidth',1.5,'LineStyle','--');
plot(t,Real_Signal_3,'LineWidth',1.5,'color','b');
hold off
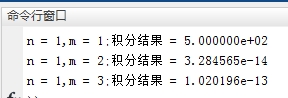
fprintf('n = 1,m = 1;积分结果 = %d\n',Int_Result3);
fprintf('n = 1,m = 2;积分结果 = %d\n',Int_Result4);
fprintf('n = 1,m = 3;积分结果 = %d\n',Int_Result5);1.仿真结果:

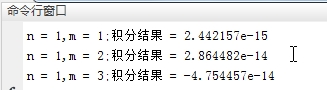
2.仿真结果:

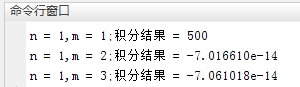
3.仿真结果:

5.总结
对三角函数正交性进行了分析,并用Matlab对正交性进行了仿真,仿真结果和理论结果一致。