蓝桥杯搜索大全
- 练功(bfs,相同步数的节点在队列中该以如何顺序摆放
- 机器人塔(最底行定则全局定,如熄灯问题)
- 卡片换位
- 存储信息
- 一维坐标和二维坐标的转化
- 迷宫与陷阱
练功(bfs,相同步数的节点在队列中该以如何顺序摆放


最典型的bfs,一般有4种移动方式,每一种都一定会向终点更接近且向终点接近的距离程度是一样的,唯一影响的是这条路上可能会有走不了的路
(.可走,*不可走)
其实主要就是 队列中 走了相同步数(有着相等step值)的节点,该怎么排列 (肯定是挨在一起的,step-1的节点们之后,step+1的节点们之前)
这里完全无阻碍,只需要考虑距离,走下这一步距离更近这一步就该走,但先以哪种方式走呢
其实这里也是 每一种都一定会向终点更接近,cur是个供于比较的‘全局’变量(走出一步的所有方式的比较)
或者说cur是在step+1操作之前的判断,同样是多走一步,假设我走了step+1步距离终点x, 你走了step+1步距离终点y,x<y,
那么如果利用优先队列存放所有的到达节点,我应该排在你前面(优先队列通过比较当前到终点的距离 (法二)
如果更贪心一些,很容易就发现,除了距离没有障碍,我们相同步数时我距离终点最近,一定是我先到达终点
于是只需要存放当前步数下距离终点最近的节点(法一)
法一
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m;
double d;
typedef struct node{int x,y,step;}node;
queue<node> Q;
bool vis[N][N];
double cal(int x,int y,int x1,int y1){return sqrt((x1-x)*(x1-x)+(y1-y)*(y1-y));
}
void bfs(){double cur=cal(1,1,n,m);while(!Q.empty()){node t=Q.front();Q.pop();int x=t.x;int y=t.y;int s=t.step;if(x==n&&y==m){printf("%d",s);return;}int rx,ry;for(int i=x;i<=x+d&&i<=n;i++){//记得判断越界for(int j=y;j<=y+d&&y<=m;j++){if(!vis[i][j]&&cal(x,y,i,j)<=d){vis[i][j]=true;if(cal(i,j,n,m)<=cur){//和普通的bfs不同的是rx=i,ry=j;
// Q.push({i,j,s+1});cur=cal(i,j,n,m);}}}}//枚举比较完 走这一步的所有方式 走完后距离终点的距离Q.push({rx,ry,s+1});}
}
int main(){scanf("%d%d%lf",&n,&m,&d);
// cin>>n>>m>>d;Q.push({1,1,0});vis[1][1]=true;bfs();return 0;
}
法二
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m;
double d;
typedef struct node{int x,y,step;double dis;bool operator<(const node & a)const{return dis>a.dis;}//别忘了优先队列默认是大顶堆(小的把大的推上去)}node;
priority_queue<node> Q;
bool vis[N][N];
double cal(int x,int y,int x1,int y1){return sqrt((x1-x)*(x1-x)+(y1-y)*(y1-y));
}
void bfs(){while(!Q.empty()){node t=Q.top();Q.pop();int x=t.x;int y=t.y;int s=t.step;if(x==n&&y==m){printf("%d",s);return;}for(int i=x;i<=x+d&&i<=n;i++){//记得判断越界for(int j=y;j<=y+d&&y<=m;j++){if(vis[i][j])continue;if(cal(x,y,i,j)>d)break;
// if(!vis[i][j]&&cal(x,y,i,j)<=d)本来可以直接这样判断,但break效率高点,继续远下去肯定都大于dvis[i][j]=true;
// rx=i,ry=j;Q.push({i,j,s+1,cal(i,j,n,m)});
// 放心入队,优先队列自然会将距离终点最近的(也一定是最短路径上的节点放在最前面)}}}
}
int main(){scanf("%d%d%lf",&n,&m,&d);
// cin>>n>>m>>d;Q.push({1,1,0,cal(1,1,n,m)});vis[1][1]=true;bfs();return 0;
}
类似于法一的思想但错误
这样也能过,可能是样例太少了,但是当即比较当即入队,同样步数的节点,只能保证降序,排在最前面的不一定是距离终点最小的(我觉得是不对的❌
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
int n,m;
double d;
typedef struct node{int x,y,step;}node;
queue<node> Q;
bool vis[N][N];
double cal(int x,int y,int x1,int y1){return sqrt((x1-x)*(x1-x)+(y1-y)*(y1-y));
}
void bfs(){double cur=cal(1,1,n,m);while(!Q.empty()){node t=Q.front();Q.pop();int x=t.x;int y=t.y;int s=t.step;if(x==n&&y==m){printf("%d",s);return;}for(int i=x;i<=x+d&&i<=n;i++){for(int j=y;j<=y+d&&y<=m;j++){if(!vis[i][j]&&cal(x,y,i,j)<=d){vis[i][j]=true;if(cal(i,j,n,m)<=cur){Q.push({i,j,s+1});cur=cal(i,j,n,m);}}}}}
}
int main(){scanf("%d%d%lf",&n,&m,&d);
// cin>>n>>m>>d;Q.push({1,1,0});vis[1][1]=true;bfs();return 0;
}
机器人塔(最底行定则全局定,如熄灯问题)


只要确定最底层的所有排列方式,整体的排列就已经确定,
因为通过AB出现的规律,只要地下俩元素确定上面的元素就确定是A还是B了
只要枚举最底层的所有排列方式,最底层有n个字母(等差数列的和已知,根据解方程得到)
1、判断相邻两个数是否相等,不要根据相等与否直接累计AB的个数,这样不会重复计数的咩?!
2、压缩数组,每次数组长度 ”减” 1,
判断相邻两个数是否相等,每次的最后一个元素,要单独累计,等到压缩数组压到长度为1 的时候,第一个就是最后一个,不用再执行压缩操作,只需要判断累计
遍历数组,一边生成长度 ”减” 1的压缩数组,一边判断并累计AB的个数,后者必须在前者之前,压缩数组会改变原本d[i]的值
#include <bits/stdc++.h>
using namespace std;
//#define int long long int
const int N=55;
int x,y,n;
int d[N];
int res=0;
void dfs(int u){if(u==n+1){
// 判断AB的个数是否吻合int sa=0,sb=0;int t=n;while(t){//有效长度 t==2,i// for(int i=1;i<=t;i++)cout<<d[i]<<" ";for(int i=1;i<t;i++){if(d[i]==0)sa++;else sb++;//改变之前计数if(d[i]!=d[i+1]){d[i]=1;}else d[i]=0;// if(d[i]!=d[i+1]){
// d[i]=1;
// sa++;
// sb++;
// }
// else if(d[i]==0){
// d[i]=0;
// sa+=2;
// }
// else {
// d[i]=0;
// sb+=2;
// }}if(d[t]==0)sa++;else sb++;//不要忘记最后一个数
// cout<<endl<<sa<<" "<<sb<<endl;t--;}
// if(d[1]==0)sa++;
// else sb++;不需要,t=1不会进行比较但是第一个就是最后一个if(sa==x&&sb==y)res++;// cout<<sa<<" "<<sb<<" end!!"<<endl;return ;}d[u]=0;//Adfs(u+1);d[u]=1;dfs(u+1); }
signed main(){scanf("%d %d",&x,&y);
// (1+n)*n/2=(x+y)
int s=2*(x+y);n=(-1+sqrt(1+4*s))/2;dfs(1);//最底层有n个字母,cout<<res;
return 0;
}是可以通过二进制数直接枚举
#include<iostream>
#include<bitset>
#include<cmath>
using namespace std;int n, m;bool check(int now, int num){int num_a = 0, num_b = 0;for(int i = num ; i >= 1 ; i--){//i是层数也是机器人个数//bitset类可以用.count()方法可快速求出二进制下1的个数//创建了一个32位的bitset, 初始化值为 nowbitset<32>bs = now;num_b += bs.count();//now里面有多少1num_a += i - bs.count();//now里面有多少0//下面开始求上一层的nownow ^= now >> 1;now &= (1 << (i - 1)) - 1;}return num_a == m && num_b == n;
}int main(){cin >> m >> n;//num是层数 //利用double转int类型向下取整得性质,由(num + 1) * (num) / 2 == n + m 推导得int num = sqrt((n + m) * 2);int ans = 0;for(int i = 0 ; i < (1 << num) ; i++){//num层的最下层是num个机器人,摆法有2的num次方种,每一种可以转化为数字iif(check(i,num))ans++;}cout << ans << endl;
}
//下面开始求上一层的nownow ^= now >> 1;now &= (1 << (i - 1)) - 1;
第一行:异或求AB
第二行:截取长度
101000110
101000110
111100101 0
0111111111
卡片换位

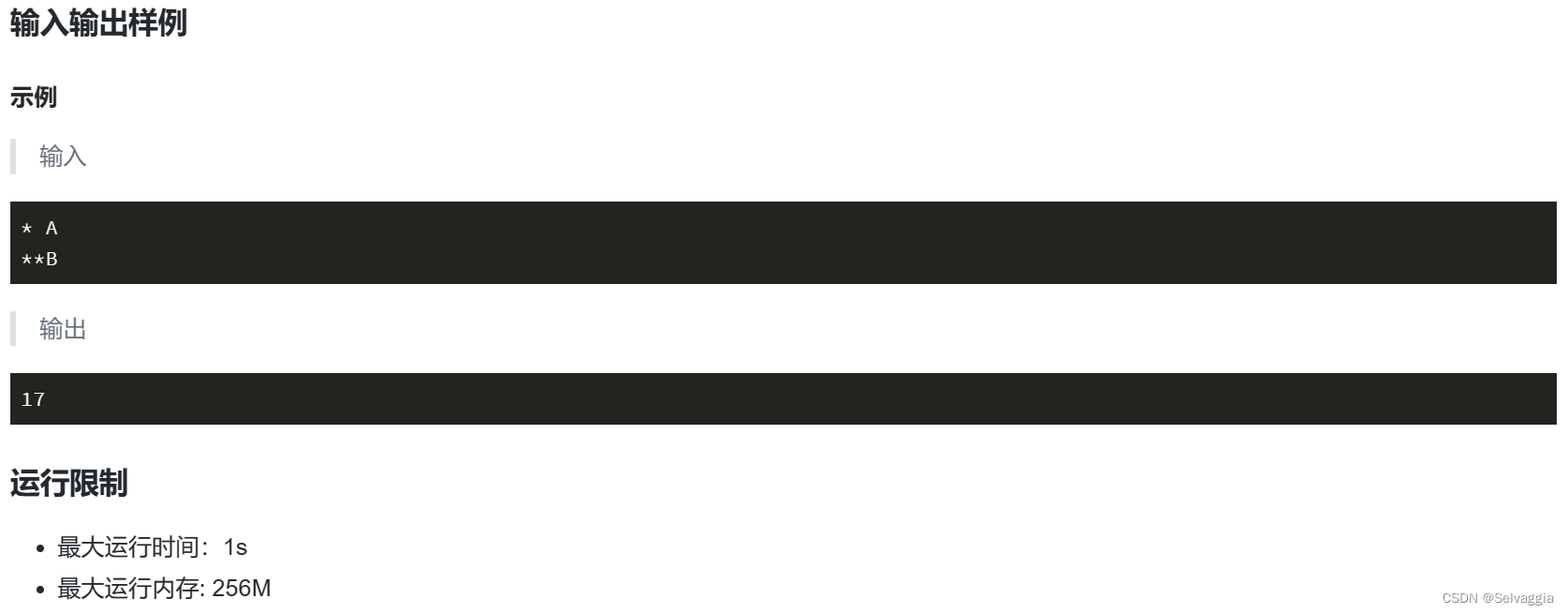
存储信息
这里的搜索不同于经典款,最短走几步到达某个终点坐标,于是存放的状态节点是 node(x,y,step)
这里的终点是AB互换的局面,于是每次存放的状态节点应该是整个局面的表示(这里只有2*3的size)完全可以用一个字符串表示全局,(像飞行员兄弟,切换开关开冰箱那道题(4*4),直接用一个二进制数表示全局就够了)
题目思想:
定位当前空格的所在位置,向四个方向一直探索 将空格与探索到的位置上的数据 互换
当即将要到达新的局面,需要避免重复循环相同的局面(相当于当经典款中某个坐标不能走两次用二维vis判重),这里只好用map<string,bool>或者set判重!
实时判断是否已经将 关羽 和 张飞互换位置了
至于存储结构,需要获得的信息有哪些?:A,B,’ ’ 的位置(为了判断是否已经成功互换位置,为了继续交换 ’ ’ 和其他),全局的string表示(为了防止循环出现局面),走到当前局面已经交换了多少次step)
但是稍加思索就发现,A,B,’ ’ 的位置这些信息 都包含在 全局的string表示中,即可以通过局面string进行查找得到(string的find函数)
一维坐标和二维坐标的转化
为了查找全局string中的 A,B,’ ’ 的位置这些信息 ,全局必须存放在一个字符串中这就涉及到 一维坐标和二维坐标的转化
(下标从0开始,3为列数)
将 一维下标 [K] 转换成二维下标:[k / 3, K % 3]
将 二维下标 [x, y] 转换成一维下标:[x * 3 + y]
#include<bits/stdc++.h>
using namespace std;//为什么要转化到二维,四个方向的搜索,以及搜索不越界
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};
int sA,sB;
bool inside(int x,int y){return x>=0&&y>=0&&x<2&&y<3;
}typedef struct node{string state;int step;
}node;
queue<node> Q;
map<string,bool> vis;
int bfs(){while(!Q.empty()){node t=Q.front();Q.pop();string s=t.state;int step=t.step;int sa=s.find('A');int sb=s.find('B');if(sa==sB&&sb==sA)return step;int pos=s.find(' ');int xspace=pos/3;int yspace=pos%3;for(int i=0;i<4;i++){int x=xspace+dx[i];int y=yspace+dy[i];if(!inside(x,y))continue;string str=s;swap(str[x*3+y],str[pos]);if(vis[str])continue;vis[str]=true;Q.push({str,step+1});}}
}
signed main(){string s1,s2;
// cin>>s1>>s2;getline(cin, s1);getline(cin, s2);string s=s1+s2;
// 获取最初的AB位置sA=s.find('A');sB=s.find('B');Q.push({s,0});cout<<bfs();return 0;
}
* A
**B
对于这种样例,输入整行的包含空格的字符串,读取整行用getline(cin,s1)
cin只能读取没有空格分隔的连续的字符串
string s1,s2;
// cin>>s1>>s2;getline(cin, s1);getline(cin, s2);
迷宫与陷阱

输入输出样例
输入
5 3
...XX
##%#.
...#.
.###.
.....
输出
10
vis数组是三维的噢~ 从不同的路到达同一坐标但是无敌步数不同 应该算作不同的状态,同一坐标上,拥有更多的无敌步数可能走得更远
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
char a[N][N];
bool vis[N][N][15];
int k,n;
//为什么要转化到二维,四个方向的搜索,以及搜索不越界
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};bool inside(int x,int y){return x>=0&&y>=0&&x<n&&y<n;
}typedef struct node{int x,y;int step;int wd;node(int x,int y,int s,int wd):x(x),y(y),step(s),wd(wd){}
// bool operator<(const node & p)const{
// if(step==p.step)return wd<p.wd;
// else return step>p.step;
// }
}node;
queue<node> Q;
int bfs(){while(!Q.empty()){node t=Q.front();Q.pop();int x=t.x;int y=t.y;int step=t.step;int wd=t.wd;if(x==n-1&&y==n-1){return step;}for(int i=0;i<4;i++){int cx=x+dx[i];int cy=y+dy[i];if(inside(cx,cy)&&a[cx][cy]!='#'){if(a[cx][cy]=='%'){
// 之后如果再次到达该格子不会获得无敌状态了
// a[cx][cy]=='.';if(!vis[cx][cy][k]){vis[cx][cy][k]=true;Q.push(node(cx,cy,step+1,k));}}else{if( wd>0&&!vis[cx][cy][wd-1]){vis[cx][cy][wd-1]=true;Q.push(node(cx,cy,step+1,wd-1));}else if(!wd&&!vis[cx][cy][0]&&a[cx][cy]=='.'){vis[cx][cy][0]=true;Q.push(node(cx,cy,step+1,0));}}}}}return -1;
}
signed main(){cin>>n>>k;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>a[i][j];}}
// cout<<"hhh";Q.push(node(0,0,0,0));vis[0][0][0]=true;//不同的wd数时可以重复到达相同坐标上吗,可以cout<<bfs();return 0;
}
注意点:
一、bfs或者dfs探索路径的时候,往往从坐标(x,y) 处拥有的状态的基础上,一个循环探索k种可能性,切记切记,循环中途不要改变 坐标(x,y) 处拥有的状态,这是路的起点,别的路还得在起点的基础上开始呢
二、
bool operator<(const node & p)const{if(step==p.step)return wd<p.wd;else return step>p.step;}
我在想相同步数的节点在队列中要不要讲究摆放顺序呢?不用的,这里不像第一题,哎呀强行解释不下去了。。。同样的步数到达(x,y) 处,如果此时 无敌步数更大,不是更有可能用最少的步数到达终点吗?
或许最短路,需要用到优先队列,讲究摆放相同步数的节点在队列中的顺序 的判断条件只是跟距离有关?
其实用优先队列也不影响,还是可以100%AC,不确定就用吧,既然相同步数的节点无所谓排列顺序,那让我觉得更可能先到达的节点排在前面也无伤大雅
#include<bits/stdc++.h>
using namespace std;
const int N=1005;
char a[N][N];
bool vis[N][N][15];
int k,n;
//为什么要转化到二维,四个方向的搜索,以及搜索不越界
int dx[4]={0,0,1,-1};
int dy[4]={1,-1,0,0};bool inside(int x,int y){return x>=0&&y>=0&&x<n&&y<n;
}typedef struct node{int x,y;int step;int wd;node(int x,int y,int s,int wd):x(x),y(y),step(s),wd(wd){}
// bool operator<(const node & p)const{
// if(step==p.step)return wd<p.wd;
// else return step>p.step;
// }
}node;
queue<node> Q;
int bfs(){while(!Q.empty()){node t=Q.front();Q.pop();int x=t.x;int y=t.y;int step=t.step;int wd=t.wd;if(x==n-1&&y==n-1){return step;}for(int i=0;i<4;i++){int cx=x+dx[i];int cy=y+dy[i];if(inside(cx,cy)&&a[cx][cy]!='#'){if(a[cx][cy]=='%'){
// 之后如果再次到达该格子不会获得无敌状态了
// a[cx][cy]=='.';if(!vis[cx][cy][k]){vis[cx][cy][k]=true;Q.push(node(cx,cy,step+1,k));}}else if(a[cx][cy]=='X'){if(wd>0&&!vis[cx][cy][wd-1]){ vis[cx][cy][wd-1]=true;Q.push(node(cx,cy,step+1,wd-1)); } }else if(a[cx][cy]=='.'){
// wd=(wd==0)?0:wd-1;
// if(wd>0)wd--; ❌这是别的路的起始状态
// else wd=0;int tmp=(wd==0)?0:wd-1;if(!vis[cx][cy][tmp]){vis[cx][cy][tmp]=true;Q.push(node(cx,cy,step+1,tmp));}}}}}return -1;
}
signed main(){cin>>n>>k;for(int i=0;i<n;i++){for(int j=0;j<n;j++){cin>>a[i][j];}}
// cout<<"hhh";Q.push(node(0,0,0,0));vis[0][0][0]=true;//不同的wd数时可以重复到达相同坐标上吗cout<<bfs();return 0;
}