搜索

---

本校的Lazer2001 学长为我们讲了搜索（乱搞）

基础：位运算

（对于二进制数$X$）

超级基础

判断第$i$位是否为1：X&(1<<(i-1))
将第$i$位赋值为1：X|(1<<(i-1))
将第$i$位赋值为0：X&(X^(1<<(i-1)))
将第$i$位取反：X^(1<<(i-1))

感觉有点难度？

将最后一个1变成0：X-lowbit(X)=X-X&(-X)
统计1的个数：while(X) {X-=lowbit(X); num++; }
枚举子集：for(s=X;s;s=(s-1)&X)
（复杂度$n^{3}$）

bitset

其实不会
总结如下：

利用位运算压缩过的bool数组
可以对两个bitset进行正常的与、或、非、左移右移等位运算
还有一些方便的操作：any,none,count,flip
空间、时间效率都有较大提升

其实就是把很多个bool->几个long long的操作了。

例题：位运算 & bitset

1. 给定$n$个数，求它们所有子集和的异或和。$n\leqslant1000,\sum a_{i}\leqslant 10^{6}$
2. n皇后问题$n\leqslant15$

基础搜索

DFS

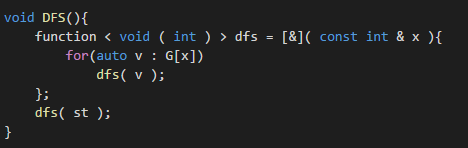
BFS

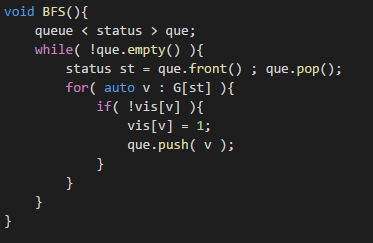
Lazer2001 前辈的神奇代码。

特殊的搜索方式

各种乱搞

双向DFS搜索

考虑一个问题的解空间为$x^{y}$规模级别，每个解可有两段结果并起来，即可考虑利用双向DFS搜索。

$$\Theta(x^{y})\to \Theta(x^{\frac{y}{2}})*log x^{\frac{y}{2}}$$

常用于统计类搜索问题。

双向BFS搜索

考虑一个问题的解空间为$x^{y}$规模级别，每个解可有两段结果并起来，即可考虑利用双向BFS搜索。（就是复制的）

$$\Theta(x^{y})\to \Theta(x^{\frac{y}{2}})*\Theta(judge)$$

常用于最优化搜索问题。

哈希

康托展开

迭代加深搜索（IDDFS）

有限度的乱搞

例题：埃及分数

将一个分数 $\frac{a}{b}$表示成多个单位分数（不能相同）的和，要求用的分数个数尽量少，个数相同时最小的分数尽量大。$1<a<b<500$

解答

每次限制使用的分数数量
利用深度上限进行剪枝：之后的分数都严格比当前小，如果在规定步数内按照当前分数的大小都无法达到要求，则剪枝。

启发式搜索（$A^{*}$)

估价函数

决定了“搜索的顺序”
需要满足什么条件?
$f(n)=g(n)+h(n)$
$h(n)\leqslant r(n)$,其中$h(n)$为估价函数，$r(n)$为实际代价
$A^{*}$算法
只要找到解，则一定是最优解
BFS、dijistra都是（没有任何优化的)$A^{*}$算法

例题：斗地主

NOIP原题（UOJ（随机数据）/洛谷（加强版））

预处理：$n\leqslant 7$时，用HASH表（或map）直接存答案
不搜索单张，贪心打小牌。

堪称搜索神题

总结（垃圾话）

Lazer2001学长因为在SCOI2018上被电子神大卡没了了100+，(张叔叔博客）但他仍然是一位优秀的老师。他的随和给我们留下了深刻的印象。
他用了一晚上告诉我们他的经验教训，拳拳真情，令我等不禁见贤思齐（见不贤内自省）。

希望他在今后的奋斗路上，长风破浪，步步高升！