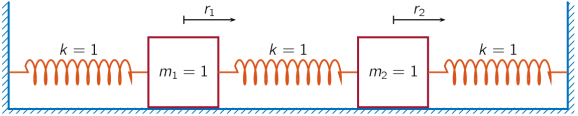编译优化之 - 向量化优化入门

1. 介绍
2. Intel高级向量扩展
3. GCC中向量化
4. ICC中向量化
5. AOCC/LLVM中向量化

1. 介绍

什么是自动向量化？

自动向量化（automatic vectorization）是自动并行化（automatic parallelization）的一种特殊情况，它将一次处理一对的标量运算转换为一次并行处理多对的向量运算。因此向量化可以显着加速一些带循环的程序运算，尤其是在大型数据集上。根据arch信息，编译器优化的目标可以是Intel或AMD处理器中的SSE*、AVX/AVX2或更高级的指令，或ARM处理器中的NEON指令。
默认情况下，GCC、ICC或AOCC/LLVM编译器中都启用了部分自动向量化功能。这些指令受运行时检查保护，即运行时检查机器是否支持该指令集，如果不支持则使用其它的指令集。

什么是SIMD指令？

SIMD（Single instruction, multiple data）单指令多数据技术能对程序中数据进行并行处理，提高吞吐量。它将原来需要多次装载的数据一次性装载到向量寄存器，即SIMD指令允许在一个步骤中处理多个数据。现代的CPU设计都包括SIMD指令，以提高多媒体程序和科学计算程序的性能，但SIMD与利用线程的SIMT不同。SIMD指令的首次使用是在1966年，它一般分为两种：

手工向量化：通过内嵌汇编码或编译器提供的内函数来添加SIMD指令。
自动向量化：利用编译器分析串行程序中控制流和数据流的特征，识别程序中可以向量执行的部分，将标量语句自动转换为相应的SIMD向量语句。

机器支持哪些指令集？

cat /proc/cpuinfo

本机cpu支持的simd指令集如下：
cpu

gcc -c -Q -march=native --help=target

本机GCC8.2支持的simd指令集如下：
gcc

注意：向量化的操作需要机器硬件的支持！

2. Intel高级向量扩展

较早的相关英特尔SSE指令还支持各种有符号和无符号整数大小，包括有符号和无符号byte（B，8位），word（W，16位），doubleword（DW，32位），quadword（ QW（64位）和doublequadword（DQ，128位）长度。

表1：英特尔AVX后缀标记

标记	含义
[s / d]	单精度或双精度浮点
[ps / pd / sd]	打包单精度、打包双精度、标量双精度
[i / u] nnn	位大小为nnn的有符号或无符号整数，其中nnn是128、64、32、16或8
epi32	扩展打包的32位有符号整数
si256	标量256位整数

更多关于Intel Advanced Vector Extensions的信息请见：Introduction to Intel® Advanced Vector Extensions

MMX指令
MultiMedia eXtensions（MMX），MMX指令主要使用的寄存器为MM0 ~ MM7，与浮点运算不能同时进行。MMX指令能一次性地操作1个64-bit的数据、或者两个32-bit的数据、或者4个16-bit的数据、或者8个8-bit的数据。
MMX指令集的扩展包括：3DNow!、SSE、AVX
SSE指令
Streaming SIMD eXtensions（SSE），SSE指令采用了独立的寄存器组XMM0 ~ XMM7，64位模式下为XMM0 ~ XMM15，并且这些寄存器的长度也增加到了128-bit。
SSE指令的升级版包括：SSE2/SSE3/SSSE3/SSE4
AVX/AVX2指令
Advanced Vector eXtentions（AVX），AVX对XMM寄存器做了扩展，从原来的128-bit扩展到了256-bit，并从XMM0–XMM7重命名为YMM0–YMM7，仍可通过SSE指令对YMM寄存器的低128位进行操作。新指令使用英特尔所谓的VEX前缀进行编码，这是一个两字节或三字节的前缀，旨在消除当前和将来的x86/x64指令编码的复杂性。AVX2将大多数整数命令扩展为256位，并引入了融合的乘加（FMA）操作。
FMA指令
Fused-Multiply-Add（FMA），FMA指令集是128-bit和256-bit的SSE的扩展指令集，以进行乘加运算。共有两种变体：FMA4、FMA3，自2014年以来，从PILEDRIVER架构开始，AMD处理器就支持FMA3；从Haswell处理器和Broadwell处理器开始，英特尔则支持FMA3。
AVX512*指令
英特尔架构处理器支持旧式和现代指令集，从64位MMX扩展到新的512位指令AVX-512。ZMM的低256-bit与YMM混用。ZMM的前缀为EVEX。与AVX / AVX2相比，AVX-512最显着的新功能是512位矢量寄存器宽度。
其他指令
KNC等其他指令集。

Intel不同架构向量化指令集如下：

表2：部分FMA指令说明

指令	含义
VFMADD[z][P/S][D/S]	乘法加法融合指令：A = r1 * r2 + r3（packed/scalar of double/single）
VFMSUB[z][P/S][D/S]	乘法减法融合指令：A = r1 * r2-r3（packed/scalar double/single）
VFNMADD[z][P/S][D/S]	乘法加法融合的负指令：A = -r1 * r2+r3（ packed/scalar double/single）
VFNMSUB[z][P/S][D/S]	乘法减法融合的负指令： A = -r1 * r2-r3（packed/scalar double/single）
VFMADDSUB[z]P[D/S]	乘法与加减法交替的融合指令，奇数索引：A = r1 * r2 + r3，偶数索引：A = r1 * r2-r3（packed double/single）
VFMSUBADD[z]P[D/S]	乘法与加减法交替的融合指令，奇数索引：A = r1 * r2-r3 ，偶数索引：A = r1 * r2+r3（packed double/single）

其中[z]代表字符串132或213或231，对应操作数A，B，C的使用顺序：

132是A = AC + B
213是A = AB + C
231是A = BC + A

3. GCC中向量化

GCC8.2.0中关于向量化操作的选项有：-ftree-loop-vectorize、-ftree-slp-vectorize、-ftree-loop-if-convert、-ftree-vectorize、-fvect-cost-model=model、-fsimd-cost-model=model。前两个向量化选项默认情况下在-O3中已启用，这里不一一说明。

具体每个选项的使用及详细介绍请见：https://gcc.gnu.org/onlinedocs/gcc-8.2.0/gcc/Optimize-Options.html#Optimize-Options

3.1 示例

使用的示例代码如下：

// vect.c
int main()
{int N = 1000;int a[N], b[N], c[N];for (int i = 0; i < N; i++) {b[i]=c[i]=i;a[i] = b[i] + c[i];}for (int i = 0; i < N; i++) {a[i] = a[i] + a[i];}printf("%d\n",a[100]);return 0;
}

如何知道一个循环是否启用了向量化？ gcc中可使用-fopt-info-vec-optimized或-fopt-info-vec命令来查看，操作如下：
gcc1
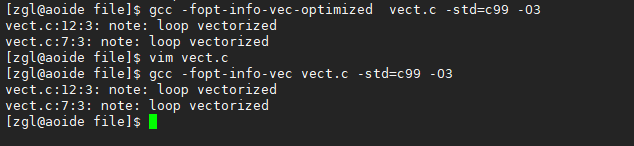
或使用-fopt-info-vec-all选项记录下所有信息，并保存到一个文件，方便查看，如下所示：
gcc2
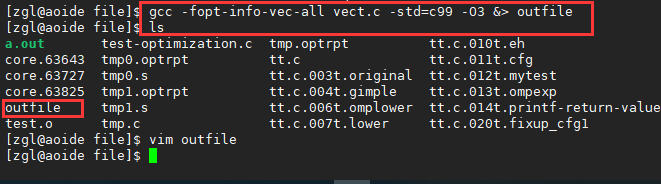
GCC中向量化操作功能有较多限制，比如：

循环中有较多条件语句，函数调用等，复杂的cfg。这样做不了向量化优化
嵌套循环中，外层循环的索引参与内部循环计算，导致无法向量化优化
其他一些特性

假若想显式的指定gcc采用什么向量化进行编译（前提是硬件支持），可参考如下操作：

gcc -O3 -march=core-avx2 vect.c -std=c99 -S -o vect.s

使用-march=core-avx2指令指定采用AVX2指令集（可指定其他指令集）。部分汇编码如下：
gcc3

4. ICC中向量化

Intel编译器中可用一下几种方式生成向量化指令：

SIMD vector intrinsics
OpenMP* 4.0 (SIMD part)
Auto-vectorization
Inline assembly code

英特尔MIC架构向量化的最重要方面之一是数据对齐。例如向量加法操作，如果编译器不知道数据对齐方式（通常是这种情况是对齐方式不正确），则将迫使编译器生成效率较低的代码。因此，重要的是优化数据的对齐并适当地将信息传达给编译器。

更多关于循环矢量化优化程序的信息请见：https://software.intel.com/en-us/articles/program-optimization-through-loop-vectorization

4.1 示例

在此使用的icc18，和测试代码如下：

// tmp.c
#include<stdio.h>
int main()
{int n = 1000;int a[n],b[n];for (int i = 0; i < n; ++i){a[i] = i * 10;b[i] = a[i]+i * 10;}printf("%d\n",b[10]);return 0;
}

如何知道一个循环是否启用了向量化？ icc中可使用-qopt-report -qopt-report-phase=vec命令查看，操作如下：

icc -qopt-report -qopt-report-phase=vec -O3 tmp.c -std=c99// icc: remark #10397: optimization reports are generated in *.optrpt files in the output locationvim tmp.optrpt// 报告结果如下
Intel(R) Advisor can now assist with vectorization and show optimizationreport messages with your source code.
See "https://software.intel.com/en-us/intel-advisor-xe" for details.Begin optimization report for: main()Report from: Vector optimizations [vec]LOOP BEGIN at tmp.c(6,4)remark #15300: LOOP WAS VECTORIZED
LOOP ENDLOOP BEGIN at tmp.c(6,4)
<Remainder loop for vectorization>remark #15301: REMAINDER LOOP WAS VECTORIZED
LOOP END
===========================================================================

如上remark #15301: REMAINDER LOOP WAS VECTORIZED所示，icc对该代码启用了循环优化，部分汇编码如下所示：
icc1
如果要求编译器不要向量化特定循环，可以使用#pragma novector命令，如下：

#pragma novector 
for (int i = 0; i < n; ++i)//同样使用以上操作，生成报告如下
LOOP BEGIN at tmp.c(7,4)remark #15319: loop was not vectorized: novector directive used
LOOP END
===========================================================================

部分汇编码如下所示：
icc2

类似命令还有：

#pragma vector always
#pragma vector align

假若想显式的指定icc采用什么向量化进行编译（前提是硬件支持），可参考如下操作：

icc -qopt-report -qopt-report-phase=vec -O3 -march=core-avx2 tmp.c -S -o tmp0.s -std=c99

使用-march=core-avx2指令指定采用AVX2指令集（可指定其他指令集），-qopt-report -qopt-report-phase=vec记录向量化信息。部分汇编码如下：
icc3

5. AOCC/LLVM中向量化

LLVM有两种向量化：作用于循环的Loop Vectorizer、将代码中找到的多个标量合并为矢量的SLP Vectorizer。默认情况下已启用了两种向量化优化。
AOCC2.1中向量化相关的选项有：-enable-strided-vectorization、-enable-epilog-vectorization、-vectorize-memory-aggressively、-global-vectorize-slp、-region-vectorize、-suppress-fmas。

具体每个选项的使用及详细介绍请见：https://developer.amd.com/wp-content/resources/AOCC-2.1-Clang-the%20C%20C++%20Compiler.pdf

5.1 示例

LLVM中若想禁用Loop Vectorizer和SLP Vectorizer，可以使用命令行标志通过clang禁用它：

clang ... -fno-vectorize  ohter.c
clang ··· -fno-slp-vectorize file.c

可以使用命令行标志“ -force-vector-width”来控制矢量化SIMD宽度:

clang  -mllvm -force-vector-width=8 ...
opt -loop-vectorize -force-vector-width=8 ...

可以使用命令行标志“ -force-vector-interleave”来控制展开因子:

clang  -mllvm -force-vector-interleave=2 ...
opt -loop-vectorize -force-vector-interleave=2 ...

以上示例及说明参考自“Auto-Vectorization in LLVM”，更多详细信息请见：https://llvm.org/docs/Vectorizers.html

在此使用以下示例代码：

// tmp.c
#include<stdio.h>
int main()
{int n = 1000;int a[n],b[n];for (int i = 0; i < n; ++i){a[i] = i * 2;for(int j = 0; j<n/2;j++){b[i] = a[i]+a[j]*2;}}printf("%d\n",b[10]);return 0;
}

如何知道一个循环是否启用了向量化？ llvm中可使用-Rpass-missed=loop-vectorize命令查看，操作如下：

clang -O3 -Rpass-missed=loop-vectorize tmp.c// 得到信息如下。可知对于如上循环很多编译器是做不了向量化优化的
tmp.c:6:4: remark: loop not vectorized [-Rpass-missed=loop-vectorize]for (int i = 0; i < n; ++i)^

假如使用一下代码：

#include<stdio.h>
int main()
{int n = 1000;int a[n],b[n];for (int i = 0; i < n; ++i){a[i] = i * 2;}printf("%d\n",a[10]);return 0;
}

再使用clang -O3 -Rpass=loop-vectorize tmp.c命令查看，便得到一下结果：

tmp.c:6:4: remark: vectorized loop (vectorization width: 4, interleaved count: 2) [-Rpass=loop-vectorize]for (int i = 0; i < n; ++i)^

对于以上代码，AOCC2.1使用-Wl,-mllvm -Wl,-region-vectorize命令操作如下：

clang -O3 -Rpass=loop-vectorize tmp.c -flto -Wl,-mllvm -Wl,-region-vectorize

AOCC2.1中向量化操作与LLVM基本相似，在此不做更多介绍。

References:

SIMD自动向量化编译优化概述
https://colfaxresearch.com/skl-avx512/
https://en.wikipedia.org/wiki/Advanced_Vector_Extensions
https://llvm.org/docs/Vectorizers.html
https://developer.amd.com/wp-content/resources/AOCC-2.1-Clang-the%20C%20C++%20Compiler.pdf