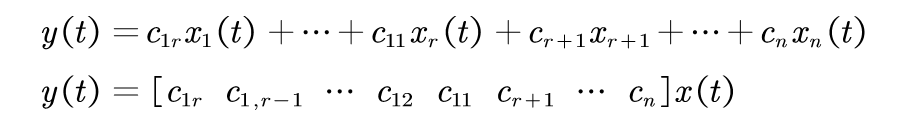前言
本文隶属于专栏《人工智能》,该专栏为笔者原创,引用请注明来源,不足和错误之处请在评论区帮忙指出,谢谢!
本专栏目录结构和参考文献请见人工智能
引子
人工智能的多个研究领域从求解现实问题的过程来看,都可抽象为一个“问题求解”过程,问题求解过程实际上就是一个搜索过程。
在搜索过程开始之前,必须先用某种方法或某几种方法的混和来表示问题。
问题求解技术主要涉及两个方面:
- 问题的表示
- 求解的方法
状态空间表示法就是用来表示问题及其搜索过程的一种方法。
问题的状态空间表示
状态空间方法:基于解答空间的问题表示和求解方法,它是以状态和算符为基础来表示和求解问题的。
主要包括:
- 状态
- 算符
- 状态空间
典型的例子:下棋、迷宫、各种游戏等。
状态( State )
状态是问题求解过程中每一步问题状况的数据结构,一般用一组数据表示:
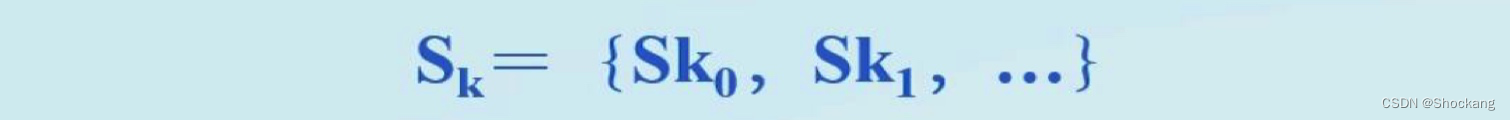
式中每个元素为集合的分量,称为状态变量。
- 每一个分量给予确定的值时,得到一个具体的状态。
- 任何一种类型的数据结构都可以用来描述状态,只要它有利于问题求解。
- 在程序中用字符、数字、记录、数组、结构、对象等表示状态。
算符( Operator )
当对一个问题状态使用某个可用操作时,它将引起该状态中某些分量值的变化,从而使问题从一个具体状态变为另一个具体状态。
- 算符可理解为状态集合上的一个函数,它描述了状态之间的关系。
- 算符可以是某种操作、规则、行为、变换、函数、算子、过程等。
- 算符也称为操作,问题的状态也只能经定义在其上的这种操作而改变。
问题的状态空间( Statespace )
用来描述一个问题的全部状态以及这些状态之间的相互关系。
状态空间常用一个三元组表示:
( S, F, G )
- S :为问题的所有初始状态的集合
- F :算符的集合
- G :为目标状态的集合
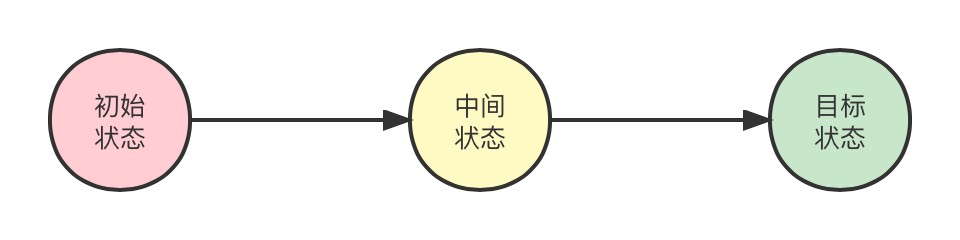
状态空间图
状态空间可用有向图来描述,图的节点表示问题的状态,图的弧表示状态之间的关系。
初始状态对应于实际问题的已知信息,是图中的根结点。
在问题的状态空间描述中,寻找从一种状态转换为另一种状态的某个操作算子序列等价于在一个图中寻找某一路径。
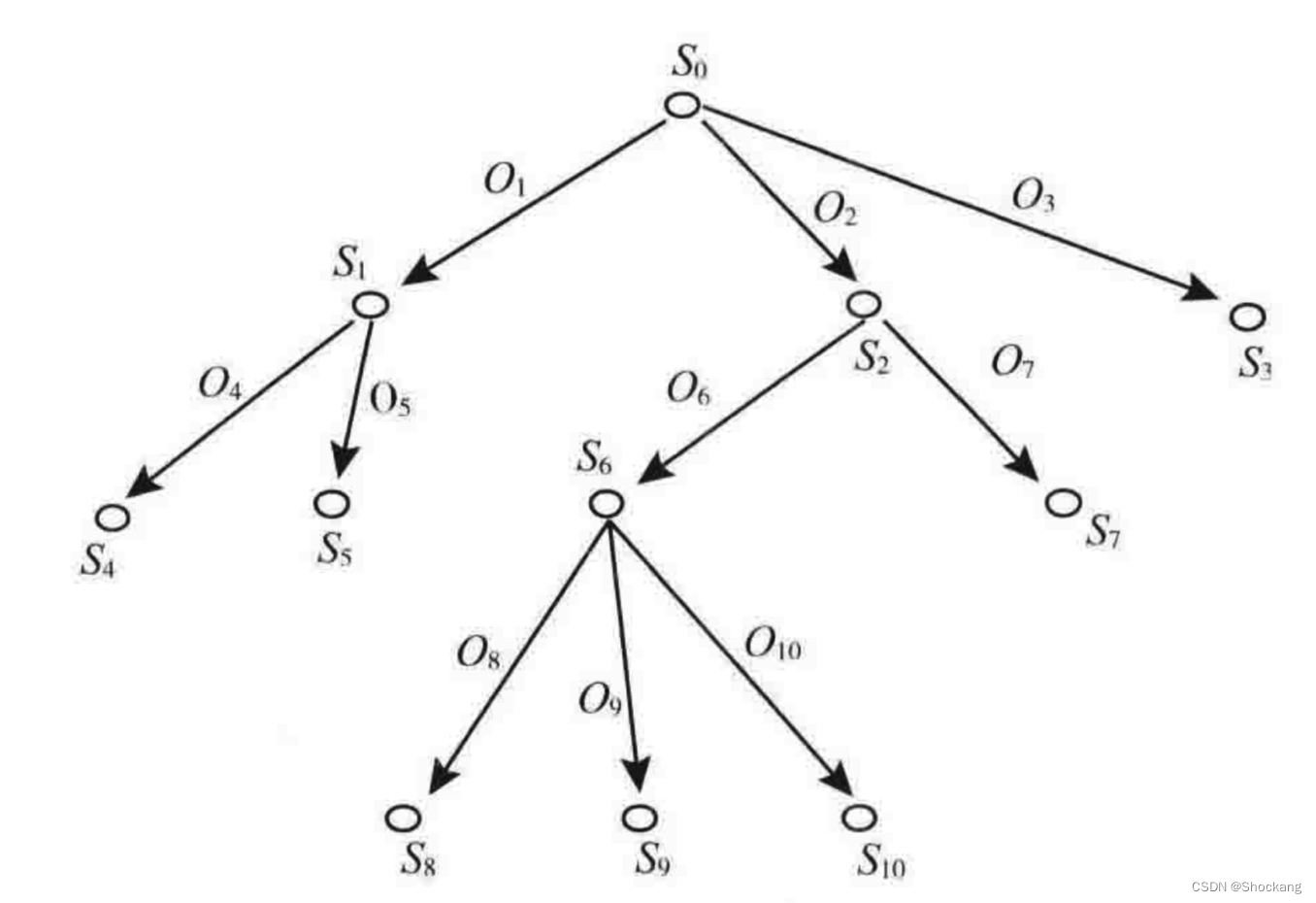
如下图所示为用有向图描述的状态空间。
该图表示对状态 S0 允许使用算符 O1 , O2 及 O3 ,分别使 S0 转换为 S1 , S2 及 S3 。
这样一步步利用操作算子转换下去,如 S10 ∈ G ,则 O2 , O6 , O10 就是一个解。
实践-八数码问题
在 3 × 3 的棋盘,摆有八个棋子,每个棋子上标有 1 至 8 的某一数字。 棋盘上还有一个空格,与空格相邻的棋子可以移到空格中。
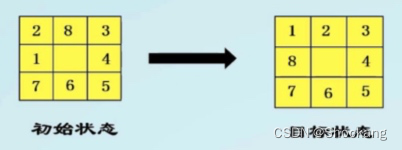
如何将棋盘从某一初始状态变成最后的目标状态?
八数码问题的状态
| X1 | X2 | X3 |
|---|---|---|
| X8 | X0 | X4 |
| X7 | X6 | X5 |
用向量 S =( X0, X1, X2, X3, X4, X5, X6, X7, X8 ) 表示状态 Xi 为变量, Xi 的值就是方格 Xi 内的数字,取值为{ 0, 1, 2 … 8 },其中 0 表示空格。
于是,向量 S 就是该问题的状态表达式。
则上图中的状态变化为:
- 初始状态: S0=(028345671)
- 目标状态: Sg=(012345678)
八数码问题的算符
制定操作算符集:
- 直观方法一为每个棋牌制定一套可能的走步:左、上、右、下四种移动。这样就需 32 个操作算子。
- 简易方法一仅为空格制定这 4 种走步,因为只有紧靠空格的棋牌才能移动。空格移动的唯一约束是不能移出棋盘。
八数码问题的状态空间图
- 从初始棋局开始,试探由每一合法走步得到的各种新棋局,然后再走一步而得到的下一组棋局。这样继续下去,直至达到目标棋局为止。
- 把初始状态可达到的各状态所组成的空间设想为一幅由各种状态对应的节点组成的图。 这种图称为状态空间图。
- 图中每个节点是它所代表的棋局。首先把适用的算符用于初始状态,以产生新的状态;算符可以看成状态空间图的边。
- 状态空间的图示形式称为状态空间图(有向图)。 其中图的节点表示状态,图的边表示算符问题求解过程就是寻求图的某一路径的问题,实际上是一个搜索过程。
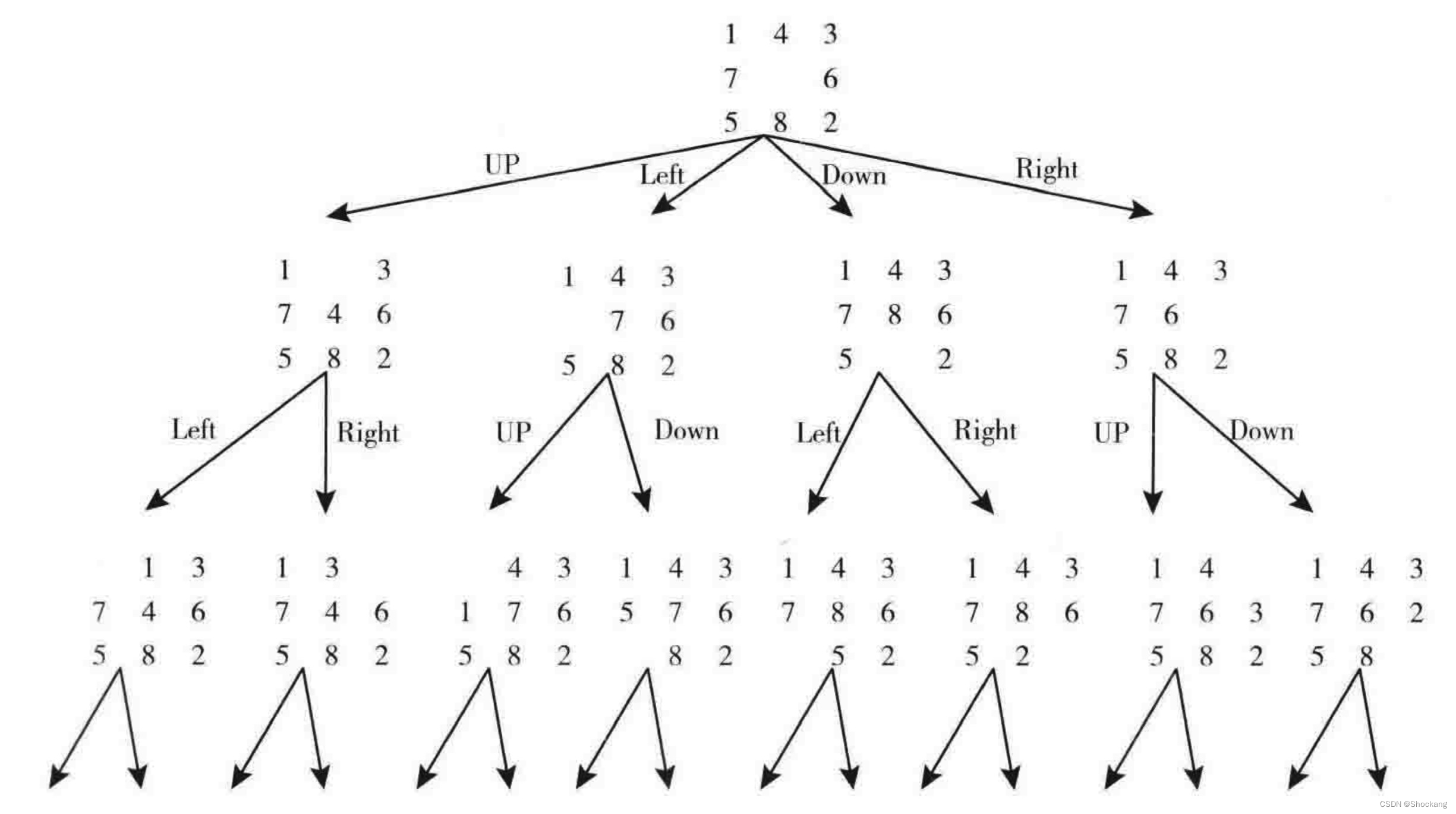
比如我们从下面这个初始棋局开始:
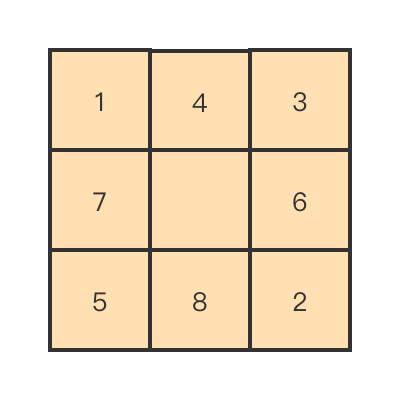
绘制的八数码问题的状态空间图(部分)如下所示: