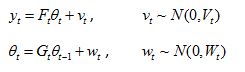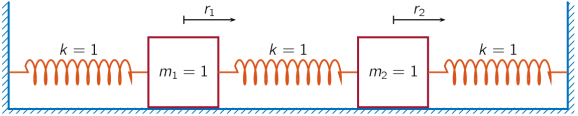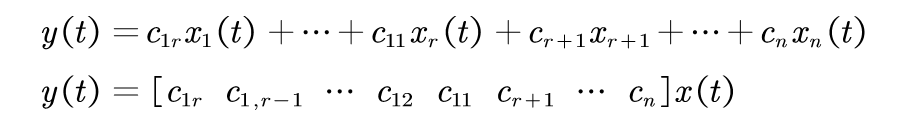状态空间模型是动态时域模型,以隐含着的时间为自变量。状态空间模型包括两个模型:
一是状态方程模型,反映动态系统在输入变量作用下在某时刻所转移到的状态;
二是输出或量测方程模型,它将系统在某时刻的输出和系统的状态及输入变量联系起来。
状态空间模型分类
状态空间模型按所受影响因素的不同分为:
(1)确定性状态空间模型
(2)随机性状态空间模型
状态空间模型按数值形式分为:
(1)离散空间状态模型
(2)连续空间状态模型
状态空间模型按所描述的动态系统可以分为:
(1)线性的与非线性的
(2)时变的与时不变的

二、系统的状态空间
离散事件随机性系统的概念是系统理论中最基本的概念。
离散事件随机性系统的状态,是指系统内部的可能运动状态和可能储能状态。系统在k=k0时刻的状态,是在k<k0时以系统内部储能的积累结果,并在k=k0时以系统要素储能的方式表现出来,还将影响系统在k>k0时的外部行为。
用随机向量序列来描述系统在任一时刻的状态向量,称为状态向量法,也称为状态空间法。状态向量表示为:

其中
 (k=1,2,1…,n)为第i个状态向量。
(k=1,2,1…,n)为第i个状态向量。 三、系统的输入输出
输入输出状态概念
引入状态向量是为了对系统内部结构进行数学描述,但在许多情况下,系统的状态是无法直接量测到的,有时甚至全部不能量测到。在实际工作中,能量测到的量之势系统的输入与输出。
输入输出变量表示
系统的输入也是随时间而变的一组变量,表示为:

称为输入向量,其分量
 (i=1,2,…,r)称为输入变量。
(i=1,2,…,r)称为输入变量。 


称为系统的量测噪声。
状态空间模型定义
状态空间模型是描述动态系统的完整模型,它表达了由于输入引起系统内部状态的变化,并由此使输出发生的变化。
状态空间模型的不同形式
如,线性时不变模型的状态方程可表示为:

输出方程为:





(4)输出矩阵或预测矩阵C为3×3维单位阵,这样输出向量或量测向量就等同于状态向量,状态空间模型:

即:



Kalman滤波简介
Kalman滤波是一种线性滤波与预测方法,原文为:A New Approach to Linear Filtering and Prediction Problems。文章推导很复杂,看了一半就看不下去了,既然不能透彻理解其原理,但总可以通过实验来理解其具体的使用方法。
Kalman滤波分为2个步骤,预测(predict)和校正(correct)。预测是基于上一时刻状态估计当前时刻状态,而校正则是综合当前时刻的估计状态与观测状态,估计出最优的状态。预测与校正的过程如下:
预测:

校正:

公式1是状态预测,公式2是误差矩阵预测,公式3是kalman增益计算,公式4是状态校正,其输出即是最终的kalman滤波结果,公式5是误差矩阵更新。各变量说明如下表:

算法实现与分析
Kalman滤波最复杂的计算应该就是公式3中的矩阵求逆,考虑到实现的方便性,采用matlab来简单实现,本文主要是分析kalman滤波中各个变量的作用和对滤波结果的影响。具体代码如下:
| 1 2 3 4 5 6 7 8 9 | function filter = Kalman(filter) %predict predict_x = filter.A * filter.x + filter.B * filter.u; filter.P = filter.A * filter.P * filter.A' + filter.Q; %correct filter.K = filter.P * filter.H ' / (filter.H * filter.P * filter.H' + filter.R); filter.x = predict_x + filter.K * (filter.z - filter.H * predict_x); filter.P = filter.P - filter.K * filter.H * filter.P; end |
在matlab中,kalman滤波实际上就是上面那5个公式,而难点却是在测试代码中针对不同问题各个变量的初始化上,下面来逐个分析。
1.建立模型,明确观测量,系统状态以及其转移方程(下面这段公式太多,通过word写好后截图)

2.初始化噪声协方差矩阵
经过上面一步,只有PQRK四个矩阵还未确定了。显然增益矩阵K是不需要初始化的,P是误差矩阵,初始化可以是一个随机的矩阵或者0,只要经过几次的处理基本上就能调整到正常的水平,因此也就只会影响前面几次的滤波结果。
Q和R分别是预测和观测状态协方差矩阵,一般可以简单认为系统状态各维之间(即上面的a和b)相互独立,那么Q和R就可以设置为对角阵。而这两个对角线元素的大小将直接影响着滤波结果,若Q的元素远大于R的元素,则预测噪声大,从而更相信观测值,这样可能使得kalman滤波结果与观测值基本一致;反之,则更相信预测,kalman滤波结果会表现得比较规整和平滑;若二者接近,则滤波结果介于前面两者之间,根据实验效果看也缺乏实际使用价值。
以上几个矩阵确定后,对于状态x,由于0时刻我们没有任何关于该系统的知识,可以使用0时刻的测量值z0来初始x0,预测从k=1开始;也可以初始化-1时刻的状态,当然这个状态实际是未知的,也就可随机取。2种方式都可以,但使用0时刻测量值来初始化状态,可以使得前面几次预测更准确。
3.实验分析
首先使用下面代码生成一组数据存在z.mat中:
| 1 2 3 4 5 6 7 8 | interval = pi/18; t = 1:interval:100*pi; len = size(t, 2); a = t + 4 * ( rand (1,len)-0.5); b = t .* sin (t/10) + 10 * ( rand (1,len)-0.5); z = [a; b]; save( 'z.mat' , 'z' ); plot(z(1,:),z(2,:), 'o' ) |
可以看出其近似为一条振幅不断增大的正弦曲线叠加一个随机噪声。绘制出来如下:

如果使用上面推导的恒定状态系统模型,代码与实验结果如下:
| 01 02 03 04 05 06 07 08 09 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 | clear close all clc dim_observe = 2; %观测值维数 n = dim_observe; %状态维数,观测状态每个维度都有1个速度,故需乘2 filter.A = eye(n);%[1,0,1,0;0,1,0,1;0,0,1,0;0,0,0,1]; filter.B = 0; filter.u = 0; filter.P = eye(n); filter.K = zeros(n); filter.H = eye(n);%[1,0,0,0;0,1,0,0]; cQ = 1e-8; cR = 1e-2; filter.Q = eye(n) * cQ; %这里简单设置Q和R对角线元素都相等,设为不等亦可 filter.R = eye(dim_observe) * cR; filter.x = zeros(n,1); %初始状态x0 load( 'z.mat' ); figure(1),subplot(2,2,1), t = 1; out = []; for i=1:size(z,2) filter.z = z(:,i); filter = Kalman(filter); plot(filter.x(1),filter.x(2), 'r*' );hold on plot(filter.z(1),filter.z(2), 'bo' ); hold on out=[out filter.x]; % pause(.5) end figure(1), str = sprintf ( 'cQ = %e, cR = %e' , cQ, cR); title(str) %画局部放大 subplot(2,2,2), plot(out(1,:),out(2,:), 'r*' );hold on plot(z(1,:),z(2,:), 'bo' ); hold on axis([120 170 80 200]) |

可以看出滤波结果完全滞后于测量数据,其根本原因在于建立的模型存在问题。
如果采用上面推导的物体运动模型则只需要修改部分代码,主要是矩阵A和H,以及其他矩阵对应的维数,具体如下:
| 1 2 3 4 5 6 7 8 | dim_observe = 2; %观测值维数 n = 2 * dim_observe; %状态维数,观测状态每个维度都有1个速度,故需乘2 filter.A = [1,0,1,0;0,1,0,1;0,0,1,0;0,0,0,1]; filter.B = 0; filter.u = 0; filter.P = eye(n); filter.K = zeros(n); filter.H = [1,0,0,0;0,1,0,0]; |
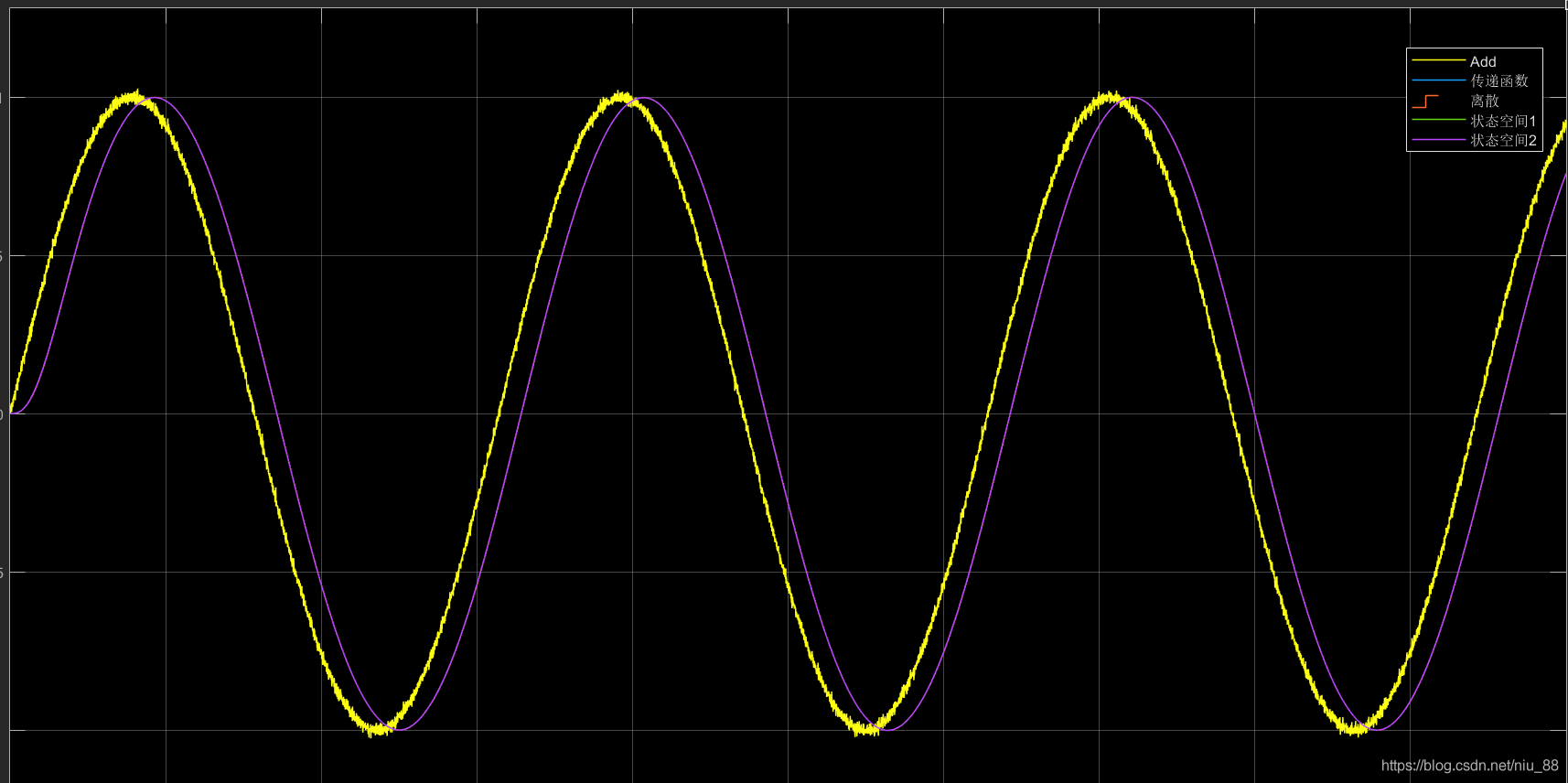
运行结果如下图,蓝色为观测数据,红色为kalman滤波数据,右侧为局部放大图。可以看出经过滤波后的数据相当平滑,这里Q和R中元素的量级分别为cQ和cR,下图结果可以看到cR比cQ多了6个数量级。

(1)
增加几组结果用于对比分析,对于的cQ和cR见图的标题。

(2)

(3)

(4)

(5)

(6)
首先看图1和2,cR与cQ大小均相差了3个数量级,而二者的比值相同,则kalman滤波结果相同。
再看图2~图6,cR/cQ在不断减小,kalman滤波结果的平滑性也在不断降低,到图5和6中,滤波结果完全和观测值相同,说明此时kalman滤波已经完全相信观测值了。原因在于cR/cQ过小,系统认为预测噪声的方差很大,不值得信赖,而观测值的噪声方差小,可信度高。
根据上面的实验结果,可以看出Kalman滤波应用中的几个问题:
1.模型建立的正确性从根本上决定了滤波效果的正确性。
上面使用物体静止模型进行滤波,结果完全不对,而使用匀速运动模型则能达到较好的效果。从根本上讲,上面的数据也不是匀速运动的,为何结果会基本正确?看看第一个使用静止模型的滤波结果,虽然我们假定了物体是静止的,但由于观测数据的作用,kalman滤波结果也会有相应的运动而不是完全静止,也就是说滤波器在不停地修正这个状态,而在匀速运动模型中,物体的速度我们认为不变,但同样地kalman滤波器也会不停地修正这个速度,滤波器中计算的速度实质的偏离了真实速度的,因此最终也会有相应的偏差,不过这个偏差在我们容许范围内,也就可以大胆使用了。
如果能确定物体是匀变速直线运动,使用相应带加速度的模型会得到更准确的效果。但是越严格的模型其适用范围也相应越小。
2.影响滤波结果平滑性的因素是cR/cQ,这个值反映了我们对于预测和观测值的信任程度;其值越大则越相信预测结果,滤波结果平滑性好;反之则越相信观测结果,滤波结果越偏向于观测值。一般我们使用kalman滤波器是为了能平滑数据的波动,因此应尽量保证cR/cQ稍大,上面的测试结果该值在1e4以上数据较为平滑。