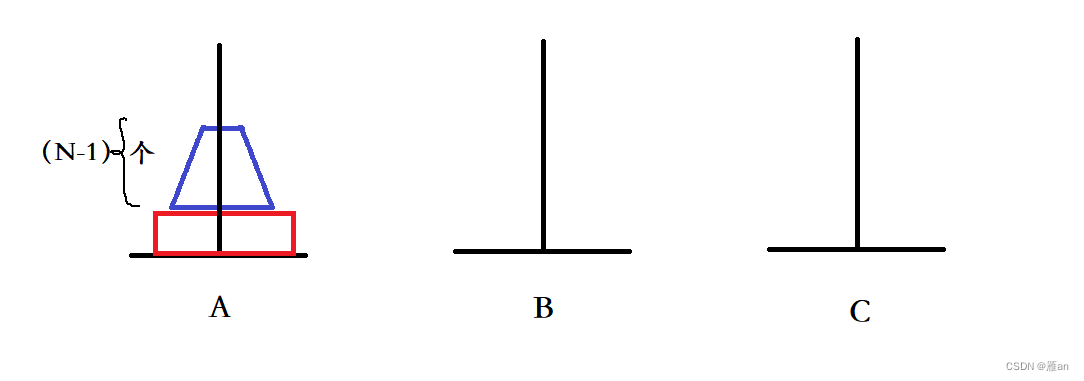关于Python实现汉诺塔问题

article/2025/9/7 16:15:29

发文声明:在刚接触汉诺塔搬盘子这个问题时候，我是很懵的，当时也没多想，后来复习的时候才深入的去剖析了一下，对于我这种小白来讲还是不太容易的，因此我写下这篇博客，来分享一下自己的学习思路和心得，希望可以帮助和我一样有困难的小伙伴们。

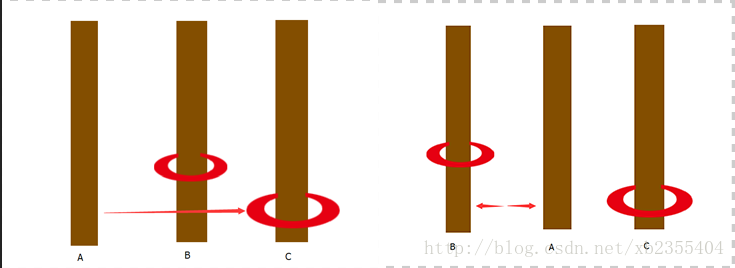
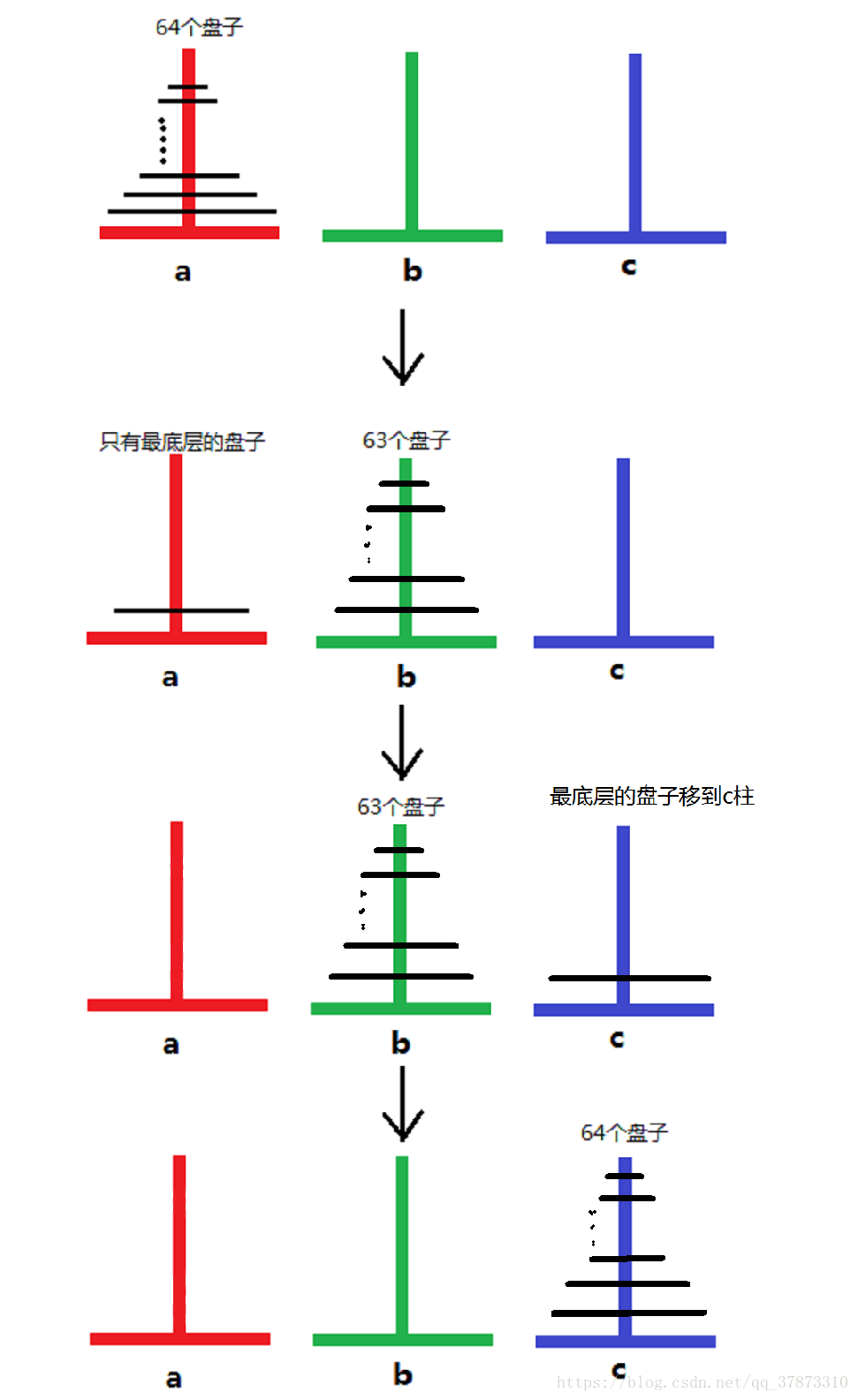
问题概述:汉诺塔问题，即搬盘子问题，是一个很经典的问题，它的大致内容是：有A、B、C三个区域在平面上横向放置，A称为起始区域，B称为中间区域，C称为目标区域，在起始区域有3个盘子，盘子的大小是从下往上依次变小的，即最小的盘子在最上面，最大的在最下面，这样摞在一起的，我们需要做的是将所有盘子一个一个地从A起始区域的盘子搬到C目标区域，过程中始终保持大盘子在下，小盘子在上，最我们需要表示出搬运步骤及搬运步数。

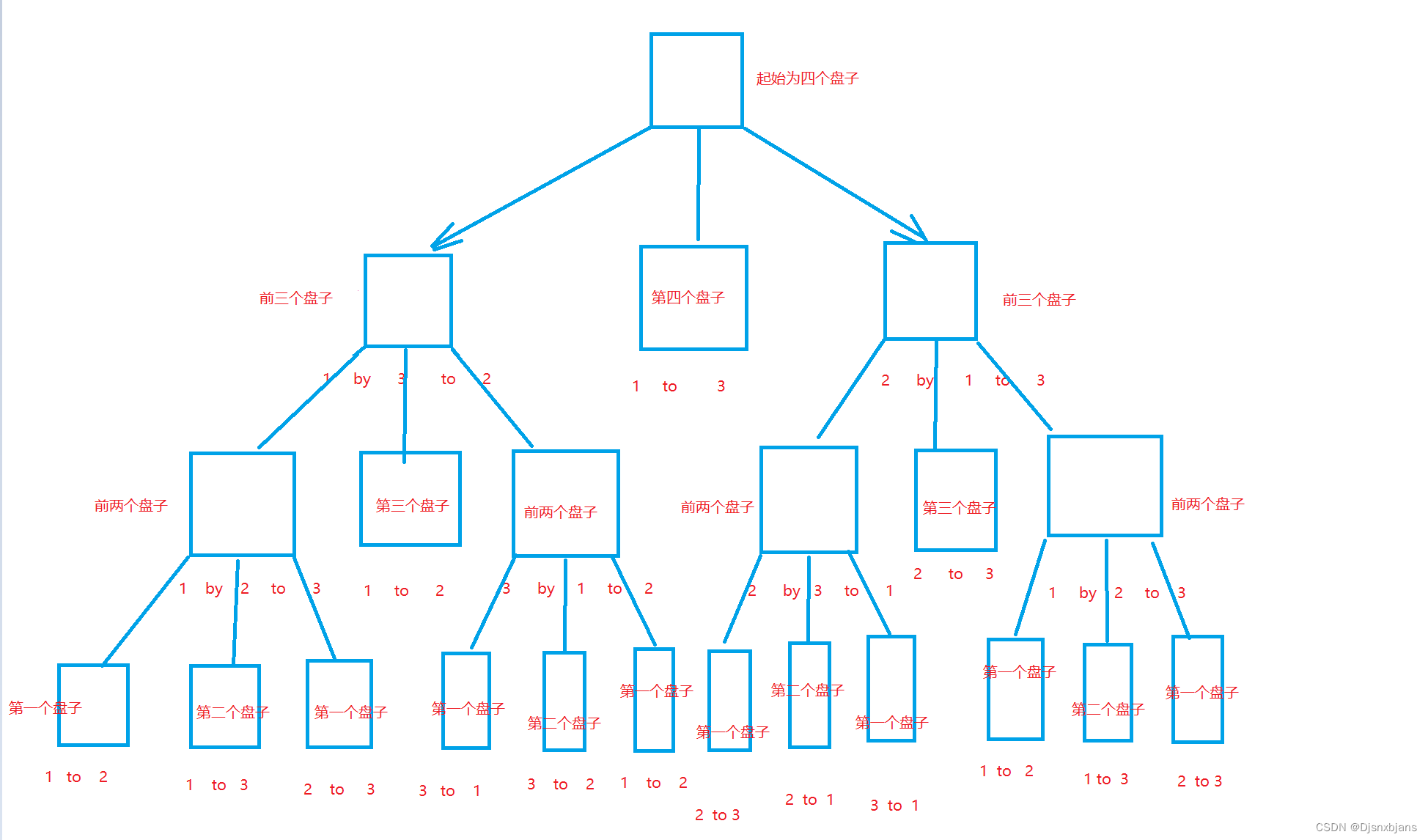
问题解答：我做这类问题的方法是递归法。递归法，递归法关注的是基例和链条。基例就是存在一个或多个不需要再次递归的条件，链条就是计算过程中的递归链条，简单理解递归法就是在函数内部调用函数本身。历史上有很多典型的问题都是可以用递归法解决的，例如阶乘问题，n = n * （n-1）！，基例是当n等于1时值为1；斐波那契数列，F（n）= F（n-1）+ F（n-2），基例是当n等于1和2时值是1，等等等等问题。对于这道题来说，我们用递归法首先应该想到递归链条。假设有3个区域ABC，A起始区域上有n个盘子需要搬到C目标区域上，首先我们将这n个盘子由上到下标号为1、2、3........n号盘子，然后我们可以先将A区域中上面的n-1个盘子借助C目标区域搬到B中间区域，紧接着再把A区域中的第n号盘子，也就是最大的那个盘子放到C区域上，这样我们就完成了第一步。（PS：我们不需要考虑如何将n-1个盘子搬到B区域的操作是如何完成的）紧接着我们将B区域剩余的n-1个盘子借助A起始区域搬到C目标区域上，这就完成了搬运任务。我们需要将每一步的搬运步骤打印出来，并统计搬运步数。下面附上Pyhton实现代码：

#汉诺塔搬盘子问题
count = 0
def hanoi(n,src,dst,mid):  # src→起始区域  dst→目标区域  n→起始区域有n个盘子  global countif n == 1:print("将{}号盘子:{}->{}".format(1,src,dst)) #只有一个盘子直接放到目标区域count += 1else:hanoi(n-1,src,mid,dst) #将上面n-1个盘子借助目标区域搬到中间区域上print("将{}号盘子:{}->{}".format(n,src,dst)) #这里的n表示n号盘子#把第n号盘子搬到目标区域上count += 1  #步骤+1hanoi(n-1,mid,dst,src) #将中间柱子上的n-1盘子借助起始区域搬到目标区域#print函数所完成是把一个盘子从起始区域搬到目标区域的操作
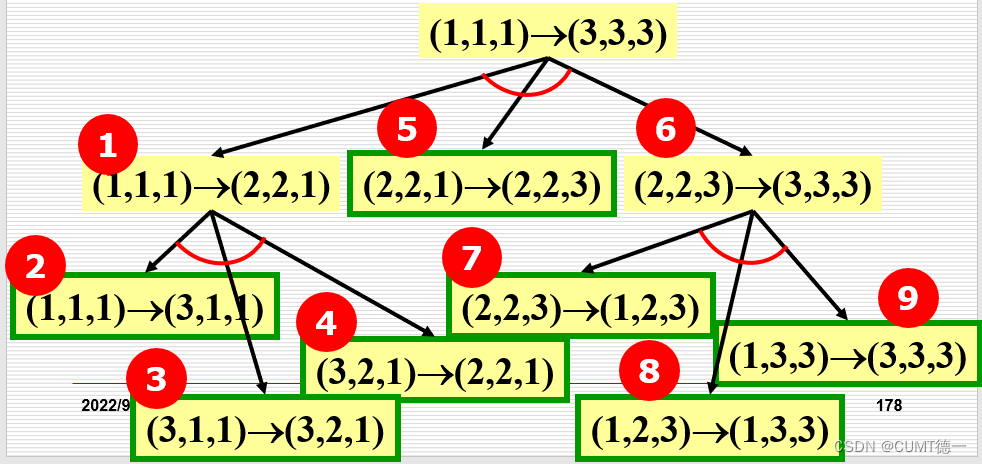
#不关注具体操作，只关注链条（基链）

下面举一个简单的例子：有三个区域ABC，A起始区域上放有3个盘子从上到下标号为1、2、3号盘子，大小由小到大。

大概长这样 ↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑↑

首先我们调用函数：

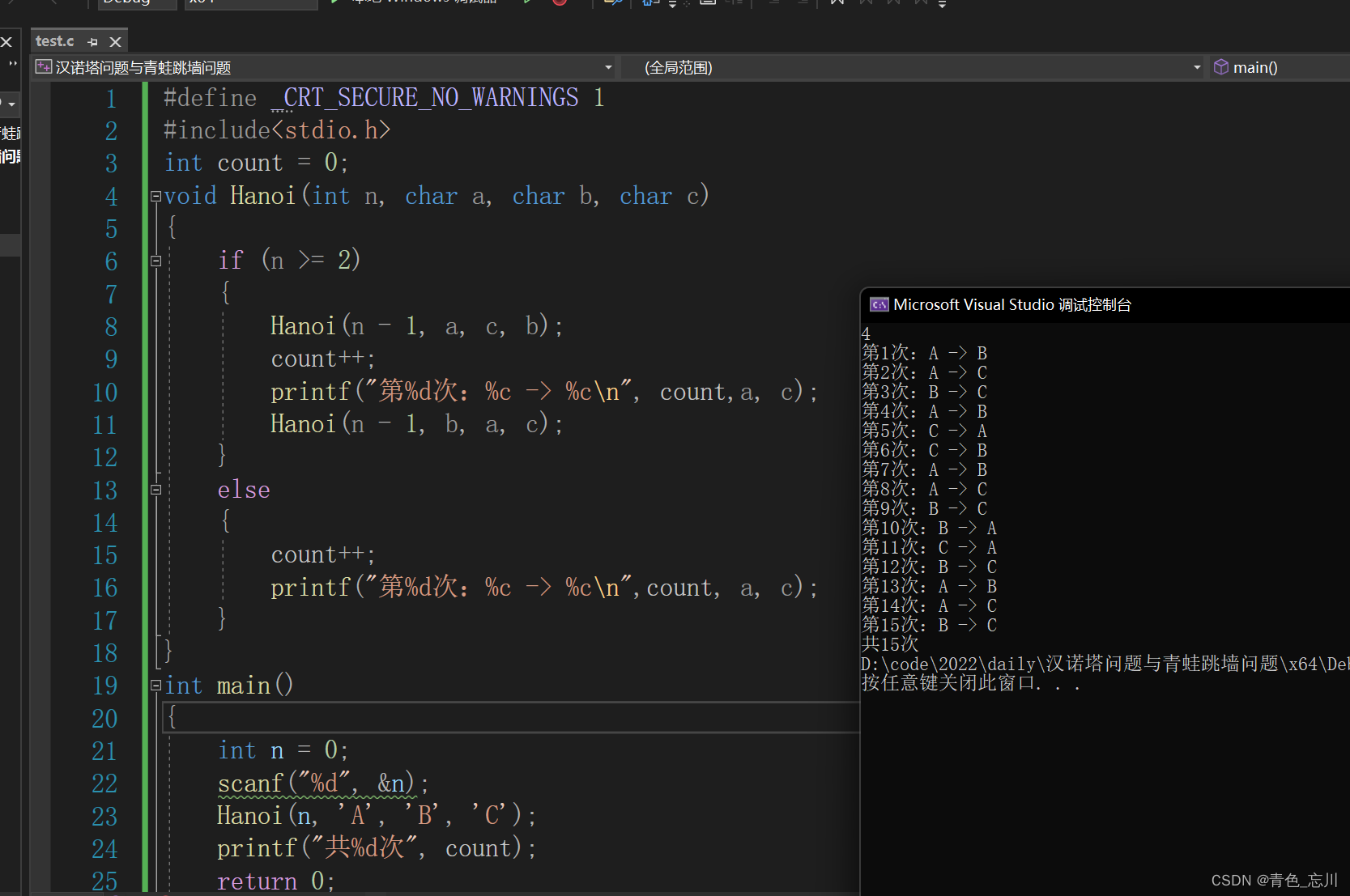
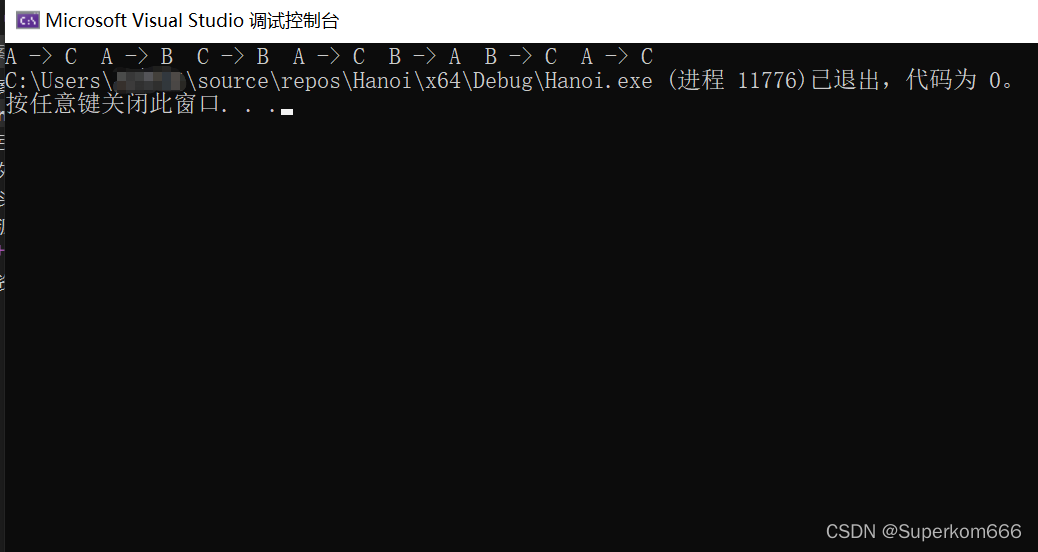
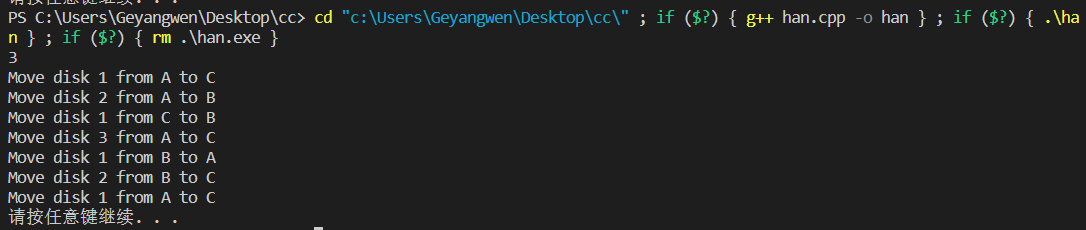
hanoi(3,"A","C","B")print("一共需要",count,"步")

函数内部语句块中文解释流程：在函数<1>hanoi（3,A,C,B）中（这里ABC不加引号，偷个懒），第一个参数是3，进入函数内部执行else语句块的第一行，调用函数<2>hanoi（2,A,B,C），语句意思是将A区域上的1、2号盘子借助C区域搬到B区域上，该函数参数为2，继续进入函数内部执行else语句块中的第一行调用函数hanoi（1,A,C,B），语句意思是将A区域上的1号盘子借助B区域搬到C区域上，该步函数参数为1，直接执行if语句块内容，打印（将1号盘子：A→C）。紧接着执行<2>函数的else语句块中的第二行（format（2,A,B）），打印（将2号盘子：A→B），然后执行<2>函数else语句块的第四行，调用函数hanoi（1,C,B,A），直接打印（将1号盘子：C→B），至此，调用的<2>函数执行完毕；紧接着执行<1>函数else语句块的第二行内容（format（3,A,C）），打印（将3号盘子：A→C），至此，已经将最大的3号盘子放到了目标区域上。然后执行<1>函数else语句块中第四行（函数的最终步骤），调用函数<3>hanoi（2,B,C,A），语句的意思是将B区域上的1、2号盘子借助A区域搬到C区域上（做完这步即结束任务），继续进入<3>函数内部，参数为2，执行else语句块第一行，调用函数hanoi(1,B,A,C)，直接打印（将1号盘子:B→A），再执行else语句块第二行format（2,B,C）,打印（将2号盘子：B→C），最后执行else语句块的第四行，调用函数hanoi(1,A,C,A),打印（将1号盘子：A→C），至此结束整个函数调用。