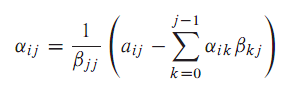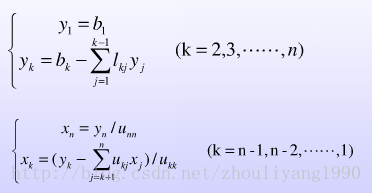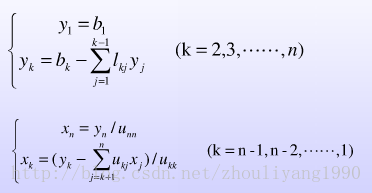LU分解初步

       矩阵的LU分解主要用来求解线性方程组或者计算行列式。在使用初等行变换法求解线性方程组的过程中，系数矩阵的变化情况如下：

       由上可知：

      ，其中U就是上面矩阵A经过行变换后的上三角矩阵，Eij表示将i行元素与j行元素互换的初等矩阵；Eij(k)表示将i行元素的k倍加到j行上。

      因此：

      如果方阵A可以分解成单位下三角矩阵L与上三角矩阵U的乘积，则式A=LU称为A的LU分解或三角分解。

LU分解定理

      那么什么样的矩阵才有LU分解呢？

      如果n阶方阵A的各阶顺序主子式 ，即A的各阶顺序主子矩阵Ak都可逆，则存在唯一的单位下三角矩阵L与唯一的非奇异上三角矩阵U，使得A=LU。

      其中k阶顺序主子式指

     那么如何计算矩阵的LU分解呢？由上可知，存在L的可逆矩阵L'，LL' = E，因此L'A = L'LU = U；由此可以得出一般分解方法，通过对(A，E)做初等行变换得到(U，L')，再由矩阵L’得到矩阵L。

LU计算行列式

      由LU分解定理可知，满足条件的矩阵A可分解为式：A = LU。|A| = |L| |U|，而其中|L| = 1，|U| 的值即为矩阵U对角线的乘积值。因此A的行列式的值即为矩阵U对角线的乘积值。

LU解线性方程组

      以最开始的矩阵A为例，求解线性方程组：

      由A的LU分解，可得Ly = b，Ux = y来代替Ax = b求解线性方程组。

，

      分别前向计算出y的所有向量，后向计算出x的所有向量。

列选主元法

      其实上述的定理条件的约束过强了，还存在条件更弱的LU分解定理。即列主元LU分解定理：

      对n阶可逆方阵A，存在置换矩阵P、单位下三角矩阵与上三角矩阵U，使得PA=LU。

      这一定义针对的是本身不满足LU分解定理的条件，但是可以经过初等变换使其满足条件的矩阵。例如：

      对于这个矩阵，可以看出该矩阵不满足LU分解定理，因此只能求A的带置换的LU分解。即：

小主元的蝴蝶效应

浮点数系统

      这里矩阵的计算问题主要针对计算机的程序实现。IEEE于1985年发布了ANSI/IEEE Std 754-1985标准，这是使用最广泛的浮点数运算标准。在754标准中，浮点数主要由符号位、指数部分和尾数三个部分。

      其中，常用的精度等级，单精度，使用32bit存储。

      双精度，使用64bit存储。

      关于浮点数系统有几点需要注意：

• 指数偏移值（exponent bias），是指浮点数表示法中的指数域的编码值为指数的实际值加上某个固定的值，IEEE 754标准规定该固定值为，其中的ε为存储指数的比特的长度。这样就保证了可以用长度为ε个比特的无符号整数来表示所有的指数取值，这使得两个浮点数的指数大小的比较更为容易。
• 实际的浮点数系统中采用了规约浮点数与非规约浮点数。对于规约浮点数，这意味着非零浮点数x可以表示为：

      其中，1不必存储；尾数f为小数，取值为0或1，t为尾数长度；p为指数。由此可以发现对于规约浮点数来说，存在绝对值意义下与零最接近的数，即(其中p取最小值)。如果p的最小值为-1，那么最小规约数就是1/2，这样0与最小规约数之间依旧间隔1/2，这就是规约化的后果。

• 引入非规约浮点数，就是为了解决上面的问题。非规约浮点数就是用来填补绝对值意义下规约浮点数与零之间的距离。若指数部分为0，且尾数非0时，就被作为非规约浮点数解析。同时需要注意的是，非规约形式的浮点数的指数偏移值比规约形式的浮点数的指数偏移值大1。例如，最小的规约形式的单精度浮点数的指数部分编码值为1，指数的实际值为-126；而非规约的单精度浮点数的指数域编码值为0，对应的指数实际值也是-126而不是-127。

因此，在计算机上，实数集的几乎所有实数都要被映射到浮点数系统中的稀疏的浮点数集，这样就会产生舍入误差。

小主元的误差

     例如线性方程组Ax = b，其中：

                                                                    

      如果系数矩阵被扰动成，可手算知：

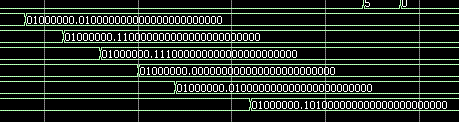
      若上述过程在计算机中进行，由浮点数运算规则可知，两数相加时，大数吃掉小数，则计算机中产生的矩阵为：

      这时会发现，且据L‘U’x=b解出的理论解，明显不再等于前面的理论解。

      这说明LU分解是稳定的，但是将LU分解用到解线性方程组上是不稳定的。究其原因，是因为中的第一个主元太小，导致第二个主元中的1与值相差悬殊，出现大数吃小数。

      为了避免上述危害，引入一种选主元手段，即在消去的过程中，通过适当的选主元，避免放大数据误差。常用的选主元技术就是列选主元法(除此之外还有全选主元法、对角选主元法和随机选主元法等)：

     对m×n阶矩阵A，在确定第k个主元()时，先从该列自主元位置(k,jk)至列尾的所有元素中选择绝对值最大的元素，与交换，然后将化为零。继续这个过程，直至将矩阵A化为行阶梯形。

特殊矩阵的LU分解

实对称正定矩阵

     Cholesky分解定理：

      设A是实对称正定矩阵，则存在唯一的可逆下三角矩阵L，使得。

      由矩阵乘法规则，可以推出实对称正定矩阵LU分解的简便计算方法(平方根法)：

1. 由可知，进而由(i ≥ 2)可知；
2. 当已求出时，由可知；
3. 当i>j时，由可知，。
   

参考资料：

《矩阵分析与计算》，李继根，张新发

IEEE 754，http://zh.wikipedia.org/wiki/IEEE_754

本作品采用知识共享署名-非商业性使用-相同方式共享 3.0 中国大陆许可协议进行许可。