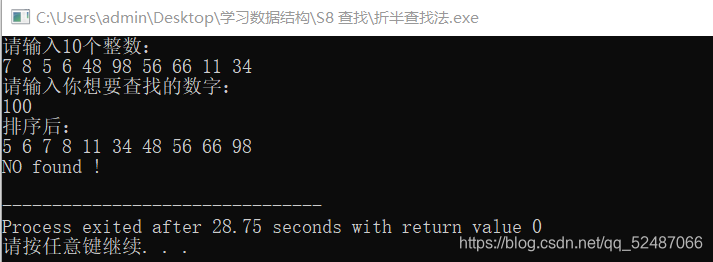
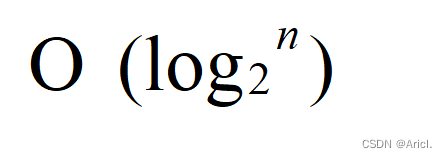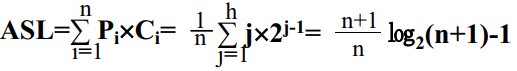二分查找法(折半查找法)：查找数组中是否包含指定元素。如果包含指定元素，则返回指定元素的index（从0开始）；如果不包含指定元素，则返回-1；

        前提：数组中的元素必须是有序的。

      原理：

        将被查找的数组分为三部分，依次是中值前、中值、中值后，将指定元素和数组的中值进行比较，如果指定元素小于中值则在（中值前）中找，如果指定元素大于中值则在（中值后）中找，如果指定元素等于中值则直接返回。依次查找后，如果不包含指定元素，则返回-1；

                  注：中值即数组中间位置的值。

        原生方法：Arrays.sort(a);：对a数组进行升序排序。

                         Arrays.binarySearch(a,b);：使用二分法查找a数组中是否包含b这个元素。

 

     两种方式：循环实现和递归实现

/*** 循环实现* 二分查找法(折半查找法)：查找数组中是否包含指定元素。* 前提：数组中的元素必须是有序的。* Arrays.sort(a);：对a数组进行升序排序。* Arrays.binarySearch(a,b);：使用二分法查找a数组中是否包含b这个元素。** @param arr 被查找的数组* @param key 指定元素* @return 如果包含指定元素，则返回指定元素的index（从0开始）；如果不包含指定元素，则返回-1；*/public static int binarySearch(int[] arr, int key) {int min = 0;int max = arr.length - 1;while (min <= max) {int mid = (min + max) >> 1;//(min + max)/2if (arr[mid] > key) {max = mid - 1;} else if (arr[mid] < key) {min = mid + 1;} else {return mid;}}return -1;}/*** 递归实现* 二分查找法(折半查找法)：查找数组中是否包含指定元素。* 前提：数组中的元素必须是有序的。* Arrays.sort(a);：对a数组进行升序排序。* Arrays.binarySearch(a,b);：使用二分法查找a数组中是否包含b这个元素。** @param arr 被查找的数组* @param key 指定元素* @return 如果包含指定元素，则返回指定元素的index（从0开始）；如果不包含指定元素，则返回-1；*/public static int binarySearch(int[] arr, int key, int startIndex, int endIndex) {if (startIndex > endIndex || startIndex < 0 || endIndex > arr.length - 1) {return -1;}int midIndex = (startIndex + endIndex) >> 1;//(startIndex + endIndex)/2if (arr[midIndex] > key) {return binarySearch(arr, key, startIndex, midIndex - 1);} else if (arr[midIndex] < key) {return binarySearch(arr, key, midIndex + 1, endIndex);} else {return midIndex;}}

      验证：

        //验证自定义的二分查找法int[] a = {};int[] b = {1, 2, 3, 4, 5, 6, 7, 8, 9};int[] c = {1, 4, 6, 7, 8, 3, -2};//循环实现int circulate1 = binarySearch(a, 0);int circulate2 = binarySearch(b, 5);int circulate3 = binarySearch(c, -2);Arrays.sort(c);int circulate4 = binarySearch(c, -2);LogUtil.e("++++++++++++++++", circulate1 + "");  //-1LogUtil.e("++++++++++++++++", circulate2 + ""); //4LogUtil.e("++++++++++++++++", circulate3 + ""); //-1LogUtil.e("++++++++++++++++", circulate4 + ""); //0//递归实现int recursion1 = binarySearch(a, 0, 0, a.length - 1);int recursion2 = binarySearch(b, 5, 0, b.length - 1);int recursion3 = binarySearch(c, -2, 0, c.length - 1);LogUtil.e("++++++++++++++++", recursion1 + "");  //-1LogUtil.e("++++++++++++++++", recursion2 + ""); //4LogUtil.e("++++++++++++++++", recursion3 + ""); //0

---------------------------------------------------------------------------------------------------------------------------

早计划，早准备，早完成。 欢迎关注！交流！Star！

GitHub：https://github.com/wangyang0313

微信公众号：一个灵活的胖子MrWang

简书：https://www.jianshu.com/u/e5e733d79b96