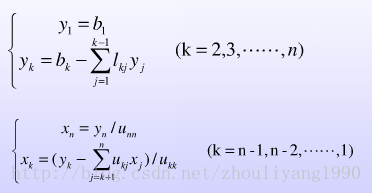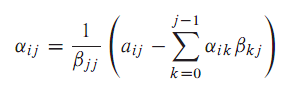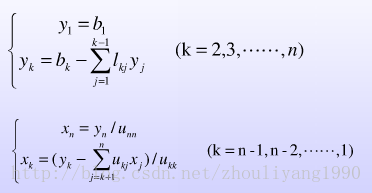LU分解
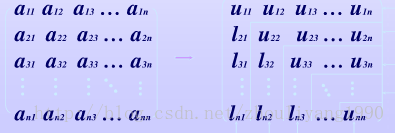
概念:假定我们能把矩阵A写成下列两个矩阵相乘的形式:A=LU,其中L为下三角矩阵,U为上三角矩阵。这样我们可以把线性方程组Ax= b写成
Ax= (LU)x = L(Ux) = b。令Ux = y,则原线性方程组Ax = b可首先求解向量y 使Ly = b,然后求解 Ux = y,从而达到求解线性方程组Ax= b的目的。
LU分解的基本思想
将系数矩阵A转变成等价的两个矩阵L和U的乘积,其中L和U分别是下三角和上三角矩阵,而且要求L的对角元素都是1;
由LU = A及对L和U的要求可以得到分解的计算公式。根据下式(独立特尔Doolittle分解):
在计算机程序中常常用到这种方法解线性代数方程组。它的优点是存储量很省。L和U中的三角零元素都不必存储,这样只用一个n阶仿真就可以把L和U存储起来。
即:下三角存储L各元素而上三角存储U的元素。
再考察公式S会发现A中任一元素aij只在计算lij(j<=i)和uij(u>=j)中用到一次,以后就不再出现了,因为完全可以利用原始数据A的单元,一个个逐次存储L或U中
的相应元素,即:
当系数矩阵A完成了LU分解后,方程组Ax = b就可以化为L(Ux) = b,等价于求解两个方程组Ly = b和Ux = y;
具体计算公式为
采用LU分解有如下特点:
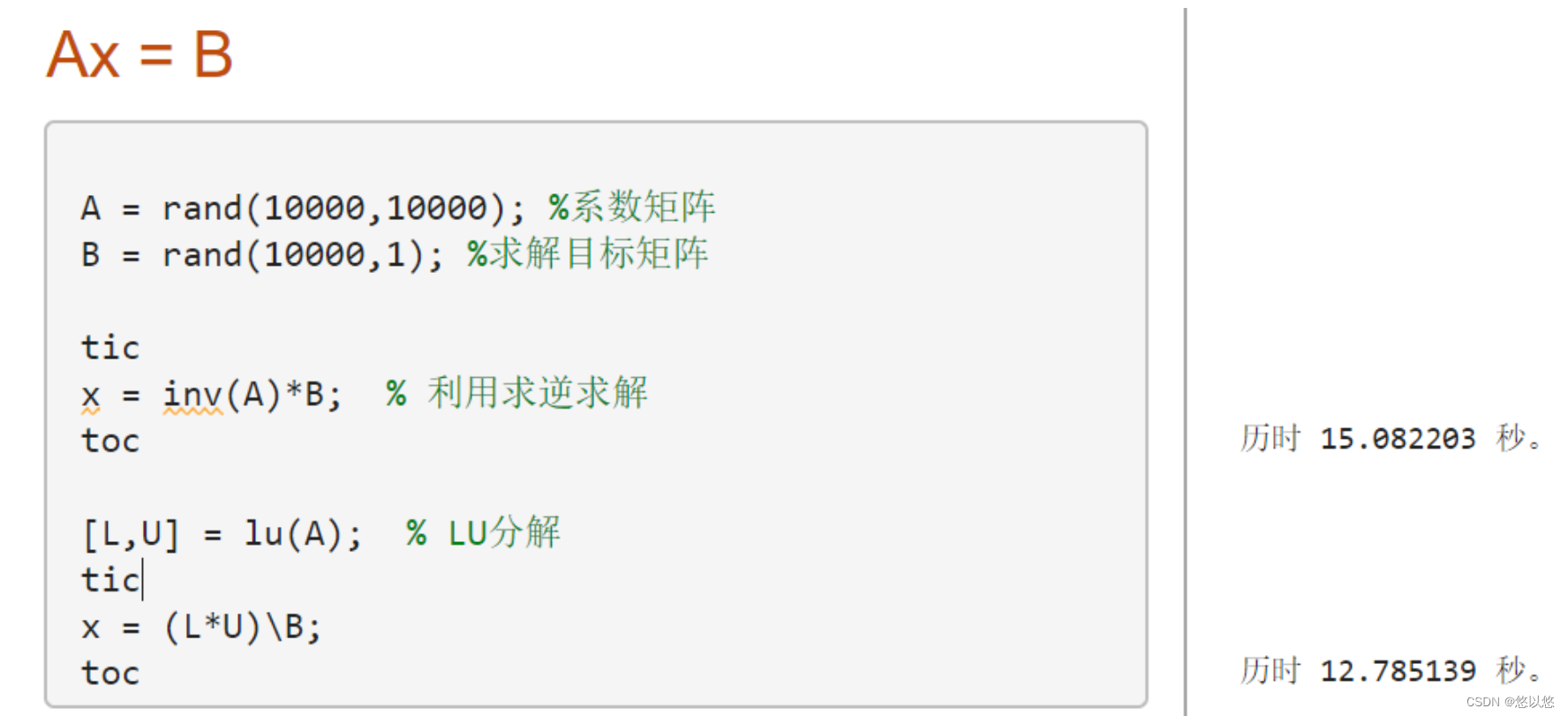
(1)LU分解与右端向量无关。先分解,后回代,分解的运算次数正比于n^3,回代求解正比于n^2。遇到多次回代时,分解的工作不必重新做,这样节省计算时间。
(2)分解按步进行,前边分解得到的信息为后边所用。
(3)【A】矩阵的存储空间可利用,节省存储。
LDLT分解法
实际问题中,当求解方程组的系数矩阵是对称矩阵时,则用下面介绍的LDLT分解法可以简化程序设计并减少计算量。
从定理可知,当矩阵A的各阶顺序主子式不为零时,A有唯一的Doolittle分解A= LU。矩阵U的对角线元素Uii 不等于0,将矩阵U的每行依次提出,
定理:若对称矩阵A的各阶顺序主子式不为零时,则A可以唯一分解为A= LDLT,这里
LT为L的转置矩阵。
当A有LDLT分解时,利用矩阵运算法则及相等原理易得计算ljk和dk的公式为
Cholesky分解
Cholesky分解是一种分解矩阵的方法, 在线形代数中有重要的应用。Cholesky分解把矩阵分解为一个下三角矩阵以及它的共轭转置矩阵的乘积(那实数界来类比的话,此分解就好像求平方根)。与一般的矩阵分解求解方程的方法比较,Cholesky分解效率很高。
Cholesky分解的条件
一、Hermitianmatrix:矩阵中的元素共轭对称(复数域的定义,类比于实数对称矩阵)。Hermitiank意味着对于任意向量x和y,(x*)Ay共轭相等
二、Positive-definite:正定(矩阵域,类比于正实数的一种定义)。正定矩阵A意味着,对于任何向量x,(x^T)Ax总是大于零(复数域是(x*)Ax>0)
Cholesky分解的形式
可记作A = L L*。其中L是下三角矩阵。L*是L的共轭转置矩阵。
可以证明,只要A满足以上两个条件,L是唯一确定的,而且L的对角元素肯定是正数。反过来也对,即存在L把A分解的话,A满足以上两个条件。
如果A是半正定的(semi-definite),也可以分解,不过这时候L就不唯一了。
特别的,如果A是实数对称矩阵,那么L的元素肯定也是实数。
另外,满足以上两个条件意味着A矩阵的特征值都为正实数,因为Ax = lamda * x,
(x*)Ax = lamda * (x*)x > 0, lamda > 0
Cholesky分解的方式
.
可以使用高斯消元法分解矩阵。过程如下:
设A = | a11 w*|
| w K|
= (R1*) * | 1 0 | * R1
| 0 K – w(w*)/a11|
其中,
R1* = | 1 0|
| w/sqrt(a11) I |
R1 = | 1 w/sqrt(a11)|
| 0 I |
如果K –w(w*)/a11大于零,那么就可以一直分解下去。因为它是一个正定矩阵的子矩阵,所以肯定可以满足。
最后:
R* = (R1*)(R2*)…(Rm*)
R =(Rm)…(R2)(R1)
因为矩阵的一半元素很相似,所以算法只需要实现一半就可以了。数据也可以只用一半,这样就节约了很多时间。同样,输出只需要一个上三角矩阵就可以了。
Cholesky分解的算法实现
R = A
For (k = 0, k < m; k++){
For(j = k; j < m; j++){
Rj,j:m = Rj,j:m – Rk,j:m Rkj / Rkk -(1)
}
Rk,k:m = Rk,k:m/ sqrt(Rkk)
}
为了节约数据空间,其中,A仅初始化为上三角矩阵。Cholesky分解的效率分析, 由于(1) 式占用了O(m)的时间,所以总计O(m^3 / 3)。