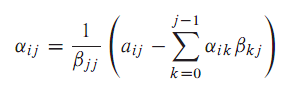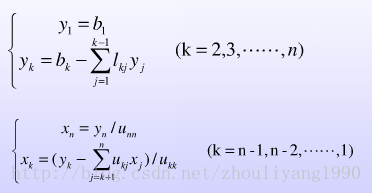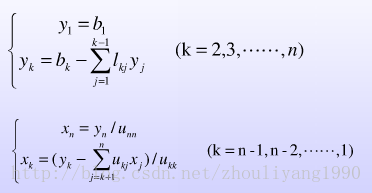一、基本介绍
前面介绍的Gauss消去法实际上做的事情是将系数矩阵A做了一个三角分解,即:
A=LU 式(1)
其中,L为单位下三角阵,U为上三角阵,该分解唯一。若A为非奇异,则U也非奇异。
实际消元过程如下所示:
第1步对应将系数矩阵和右端项
左乘一个初等变换阵,即
式(1.1)
其中,有
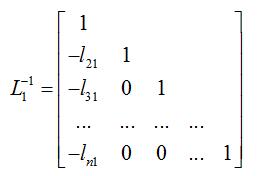
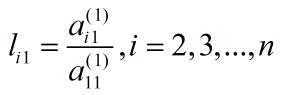
消元的第2步对应为
式(1.4)
其中,有
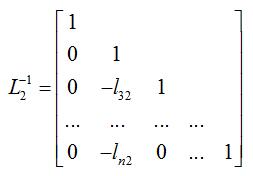
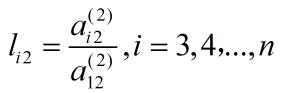
以此类推,第n-1步消元后,有:
式(1.7)
则消去过程对应的矩阵变换为
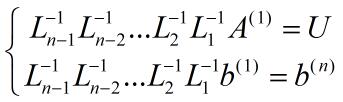
由式(1.8)可导出LU分解式(1),此处L=L1L2...Ln-1仍然是单位下三角阵,U为上三角阵,具体形式为:
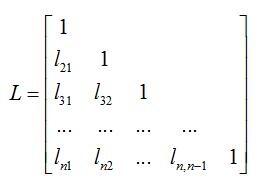
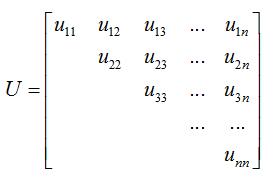
在实际编程计算的时候,只需要最终的两个矩阵L和U,此时,原方程Ax=b的求解就转化为了两个三角形方程组的求解
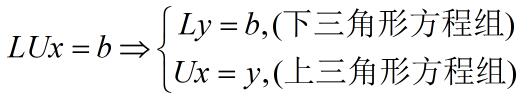
采用回代的方式即可求出中间y和结果x。
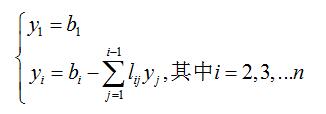
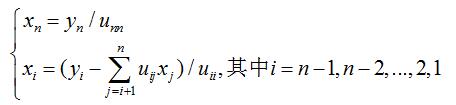
Doolittle分解可直接通过矩阵乘法导出计算过程。设A=LU,即
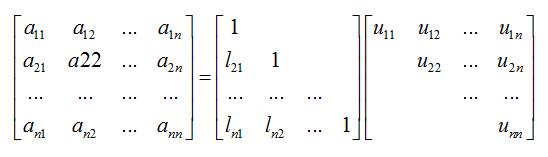
由矩阵乘法及两矩阵相等,可得
第一步,应l11=1,故u1j = a1j(j=1,2,...,n),且ai1 = li1u11,则li1 = ai1/u11,(i=2,3,...,n),由此计算出U的第1行及L的第1列元素。
一般地,若U的前i-1行及L的前i-1列元素已计算出来,则
第i步,由
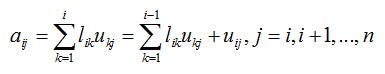
得
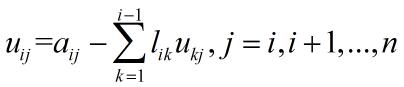
又由
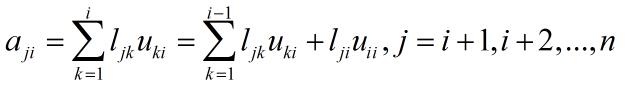
得
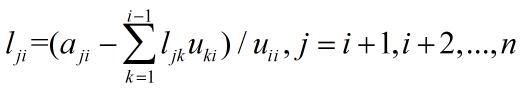
综上可得,A的LU分解公式如下
对i = 1,2,...,n
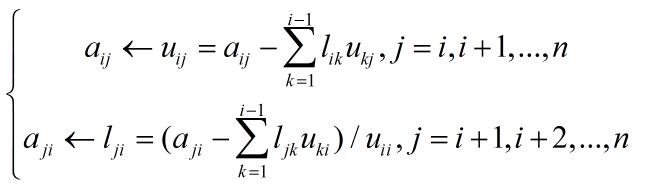
二、算法分析
在编程实现的时候,真正需要主要的公式并不多,很多看似复杂的推到,实际上只是举例几步,使得我们能够举一反三,更加清楚地理解推导式的由来。那么在这个代码中,我们需要使用到的公式包括:(1.11)、(1.12)和(1.18)。而其他公式如果无法理解其实并不影响代码的实现,只是为了更好地理解该知识点,还是建议大家自己动手推导一两步,可能会花一些时间,但肯定都是值得的。
代码实现具体步骤:
第一步:
初始化u1i,其中i = 1,2,...,n。这里初始化上三角阵的第一行的原因是在式(1.18)的累加求和中使用到i-1,当i=1时,对于uk0我们并不能找到这样的一个值。同理也需要对下三角阵的第一列进行初始化。(如果哪位小伙伴有更好的方法,欢迎留言讨论)
第二步:
采用式(1.18)递推得到整个上三角阵和下三角阵。
第三步:
采用式(1.11)回代求解中间矩阵y。
第四步:
采用式(1.12)回代求解最终结果x。
注:或许有些小伙伴对于中间复杂公式怎么求解,其实这只是一个迭代过程,只不过在迭代地过程中需要理解什么时候需要使用循环,所使用的循环初始值是多少,结束是多少,是否需要中间变量。如果理解清楚这几点,相信对于同类型的问题应该是没有任何难度问题了。如果还是没有理解清楚,欢迎私信我。
本文只给出了matlab语言的实现,不同语言实现的有一定的区别,欢迎大家使用更多不同语言来编写程序。
三、代码实现
matlab代码实现如下:
function [L_matrix,U_matrix,y_matrix,x_matrix] = LU_separetion(A_matrix, B_matirx)
% LU系数矩阵分解
% 2017-11-09 xh_scu
% inputs:
% A_matrix:输入的系数矩阵,尺寸为[n,n]
% B_matrix:输入的乘积矩阵,尺寸为[n,1]
% outputs:
% L_matrix:下三角阵,尺寸为[n,n]
% U_matrix:上三角阵,尺寸为[n,n]
% y_matrix:中间矩阵,尺寸为[n,1]
% x_matrix:结果矩阵,尺寸为[n,1]%% 第一步:初始化
% 获取n值
[row_a, col_a] = size(A_matrix);
% 初始化上三角阵的第一行
for j = 1:col_a % for-1U_matrix(1,j) = A_matrix(1,j);
end % for-1
% 初始化下三角阵的第一列
L_matrix(1,1) = 1;
for i = 2:row_a % for-2-sL_matrix(i,1) = A_matrix(i,1)/A_matrix(1,1); % 对应式(1.3)
end % for-2-e%% 第二步:前向分解计算
for i = 2:row_a % for-3-sfor j = i:col_a % for-4-stemp_sum = 0;for k = 1:i-1 % for-5-stemp_sum = temp_sum + L_matrix(i,k)*U_matrix(k,j); %对应式(1.18)-上部分的求和部分end % for-5-eU_matrix(i,j) = A_matrix(i,j) - temp_sum; % 对应式(1.18)-上部分的求差部分temp_sum_1 = 0;for p = 1:i-1 % for-6-stemp_sum_1 = temp_sum_1 + L_matrix(j,p)*U_matrix(p,i); % 对应式(1.18)-下部分的求和部分end %for-6-eL_matrix(j,i) = (A_matrix(j,i) - temp_sum_1)/U_matrix(i,i); % 对应式(1.18)-下部分的求差再求商部分end % for-4-e
end % for-3-e%% 第三步:回代计算y
x_matrix = zeros(row_a,1);
% 后向回代
% 下三角回代----计算中间矩阵Y
y_matrix(1,1) = B_matirx(1,1);
for i = 2:row_a % for-7-stemp_sum_2 = 0;for j = 1:i-1 % for-8-stemp_sum_2 = temp_sum_2 + L_matrix(i,j)*y_matrix(j,1);end % for-8-ey_matrix(i,1) = B_matirx(i) - temp_sum_2;
end % for-7-e%% 第四步:回代计算x
% 上三角回代----计算结果矩阵X
x_matrix(row_a,1) = y_matrix(row_a,1)/U_matrix(row_a,col_a);
for i=row_a-1:-1:1 % for-9-stemp_sum_3 = 0;for j = i+1:row_a % for-10-stemp_sum_3 = temp_sum_3 + U_matrix(i,j)*x_matrix(j,1);end % for-10-ex_matrix(i,1) = (y_matrix(i,1) - temp_sum_3)/U_matrix(i,i);
end % for-9-e
end四、测试分析
1)算法的准确性测试
设输入矩阵A = [2,2,3;4,7,7;-2,4,5], B = [3,1,-7]
测试代码为:
A = [2,2,3;4,7,7;-2,4,5];
B = [3;1;-7];
[L,U,Y,X] = LU_separetion(A,B);计算结果为:
L = [1,0,0;2,1,0;-1,2,1]
U = [2,2,3;0,3,1;0,0,6]
Y = [3;-5;6]
X = [2;-2;1]
与参考结果完全相等。
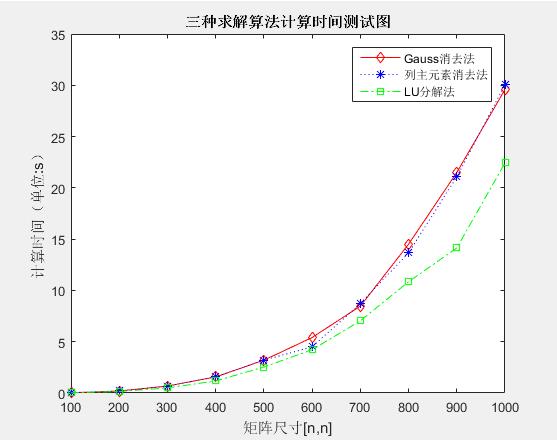
2)Gauss消去法、列主元素消去法以及LU分解法性能对比
设参数矩阵A为的元素为随机数,取值范围为[1,100],在相同输入下测试各算法的时间代价。
测试函数如下:
function [result] = test_function()
% 初始化结果矩阵[3,10]
result = zeros(3,10);
for i = 100:100:1000% 产生随机矩阵A = randint(i,i,[1 100]);B = randint(i,1,[1,100]);% 分别调用三个函数[~,time_1] = GaussElimination(A,B);[~,time_2] = MainElementElimination(A,B);[~,~,~,~,time_3] = LU_separetion(A,B);% 将得到的计算时间结果送入结果矩阵j = i/100;result(1,j) = time_1;result(2,j) = time_2;result(3,j) = time_3;
end
end注:测试函数只是进行示例说明,可能中间还存在不严谨的地方,如果有相关的意见或想法,可以留言一起探讨。
测试结果(取四位小数(四舍五入))如下表所示:
| 维数 | 100 | 200 | 300 | 400 | 500 | 600 | 700 | 800 | 900 | 1000 |
| Gauss消去法 | 0.0250 | 0.1910 | 0.6820 | 1.5680 | 3.2010 | 5.4100 | 8.4680 | 14.5070 | 21.4940 | 29.5890 |
| 列主元素消去法 | 0.0270 | 0.1970 | 0.6730 | 1.5860 | 3.2000 | 4.4970 | 8.7170 | 13.6610 | 21.0680 | 30.0600 |
| LU分解法 | 0.0200 | 0.1480 | 0.5000 | 1.1750 | 2.5320 | 4.2160 | 7.0380 | 10.8440 | 14.1410 | 22.4300 |
测试结果图例:
五、总结
1、本文分析了LU分解法的详细实现,并对编程实现进行了主要步骤的说明,给出了matlab语言的实现代码。
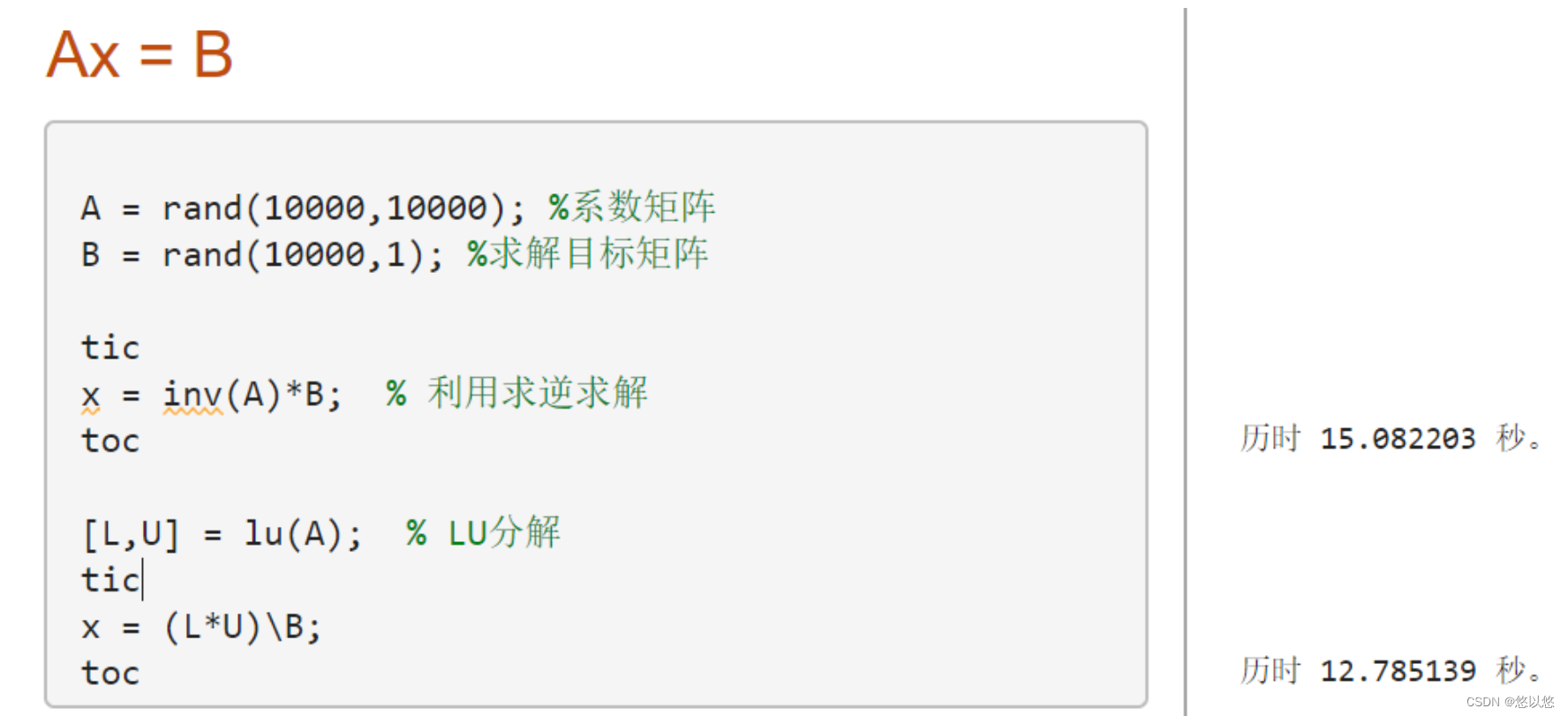
2、测试了Gauss消去法、列主元素消去法以及LU分解法的计算效率,从测试结果可以得出:在相同的输入情况下,LU分解法比前两者效率更高。