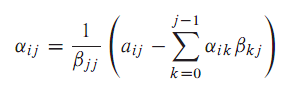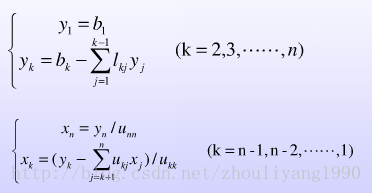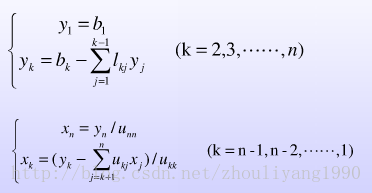线性代数笔记10——矩阵的LU分解

article/2025/8/23 19:53:38

在线性代数中， LU分解(LU Decomposition)是矩阵分解的一种，可以将一个矩阵分解为一个单位下三角矩阵和一个上三角矩阵的乘积（有时是它们和一个置换矩阵的乘积）。LU分解主要应用在数值分析中，用来解线性方程、求反矩阵或计算行列式。

什么是LU分解

　　如果有一个矩阵A，将A表示成下三角矩阵L和上三角矩阵U的乘积，称为A的LU分解。

　　更进一步，我们希望下三角矩阵的对角元素都为1：

　　一旦完成了LU分解，解线性方程组就会容易得多。

LU分解的步骤

　　上一章讲到，对于满秩矩阵A来说，通过左乘一个消元矩阵，可以得到一个上三角矩阵U。

　　可以看到，L实际上就是消元矩阵的逆。容易知道二阶矩阵的逆：

　　现在假设A是一个3×3矩阵，在不考虑行交换的情况下，通过消元得到上三角矩阵的过程是：

LU 分解的前提

　　并非所有矩阵都能进行LU分解，能够LU分解的矩阵需要满足以下三个条件：

矩阵是方阵（LU分解主要是针对方阵）；
矩阵是可逆的，也就是该矩阵是满秩矩阵，每一行都是独立向量；
消元过程中没有0主元出现，也就是消元过程中不能出现行交换的初等变换。

LU分解的意义

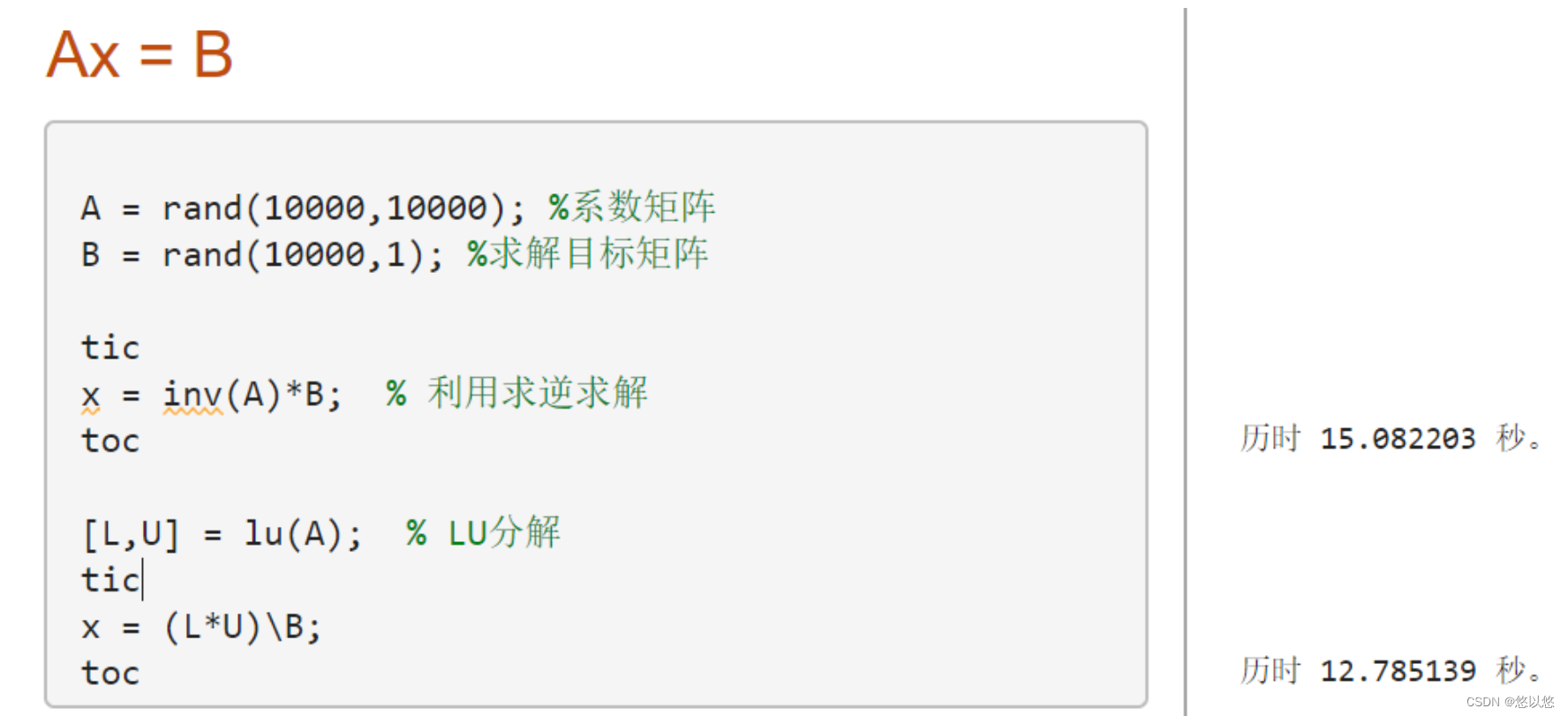
　　LU分解的意义在于求解大型方程组。一个方程组可以简化为Ax = b的形式，其中A是n阶方阵，x是未知数组成的向量，b是n×1矩阵，例如：

　　以往求解的方式有两种，一是高斯消元法，二是对A求逆，使得x = A-1b。第二种方式远比消元法复杂，先看一下消元法的计算量。假设A是n阶满秩方阵，如果不写成增广矩阵，即不考虑 b，那么第一次消元达到的效果是：

　　其中方块是A原来的元素，0是达到的效果，三角是经过消元运算后改变的元素。以第二行为例，为了使第一个元素为0，需要让第一行乘以某个数（第一行n个元素，共进行了n次乘法运算），再将第一行和第二行相加或相减（第二行n个数与第一行的n个数相加，共进行了n次加法运算）。如果把一组乘法和加法看成一次运算，那么第二行的消元共进行了n次运算；共有n-1行需要类似运算，所以第一次消元共进行了n(n - 1) ≈ n2 次运算。依次类推，第二次消元共进行了(n - 1)(n - 2) ≈ (n - 1)2 次运算……消元到最后，变成了上三角矩阵U，总运算次数是：

　　经过约n3/3次运算后可以得到上三角矩阵U，由于是增广矩阵，所以可以逐步求解x。

　　LU分解的运算过程和高斯消元类似，首先经过n3/3次运算将A变成LU，使Ax = b变成(LU)x = L(Ux) = b，再对L求逆，使得Ux = L-1b，最后求解。

　　看起来比高斯消元经历了更多的步骤，那为什么又说LU分解更快呢？在实践中，b是输出，输出又经常变动，从Ax = b频繁地变成Ax = b’，此时高斯消元就需要全部重新计算（高斯消元用增广矩阵消元，变化过程是[A, b]→[U, b’]），这对大型矩阵来说及其耗时。反观LU分解，因为它不依赖于b，所以计算一次后就可以存储U和L-1，在输出变化后也只是需要简单的相乘。实际上，由于L已经是整理过的斜对角全是1的下三角矩阵，所以用高斯-诺当消元法对L求逆非常简单。

允许行交换

　　对于A = LU，我们之前限制了行的互换，但如果不可避免的必须进行行互换，只需要把A = LU变成 PA = LU就可以了，其中P是置换矩阵。实际上所有的A = LU都可以写成PA = LU的形式，当A没有行互换时，P就是单位矩阵。上一章叙述了置换矩阵的性质，P-1 = PT，所以A = P-1LU = PTLU