相关文章
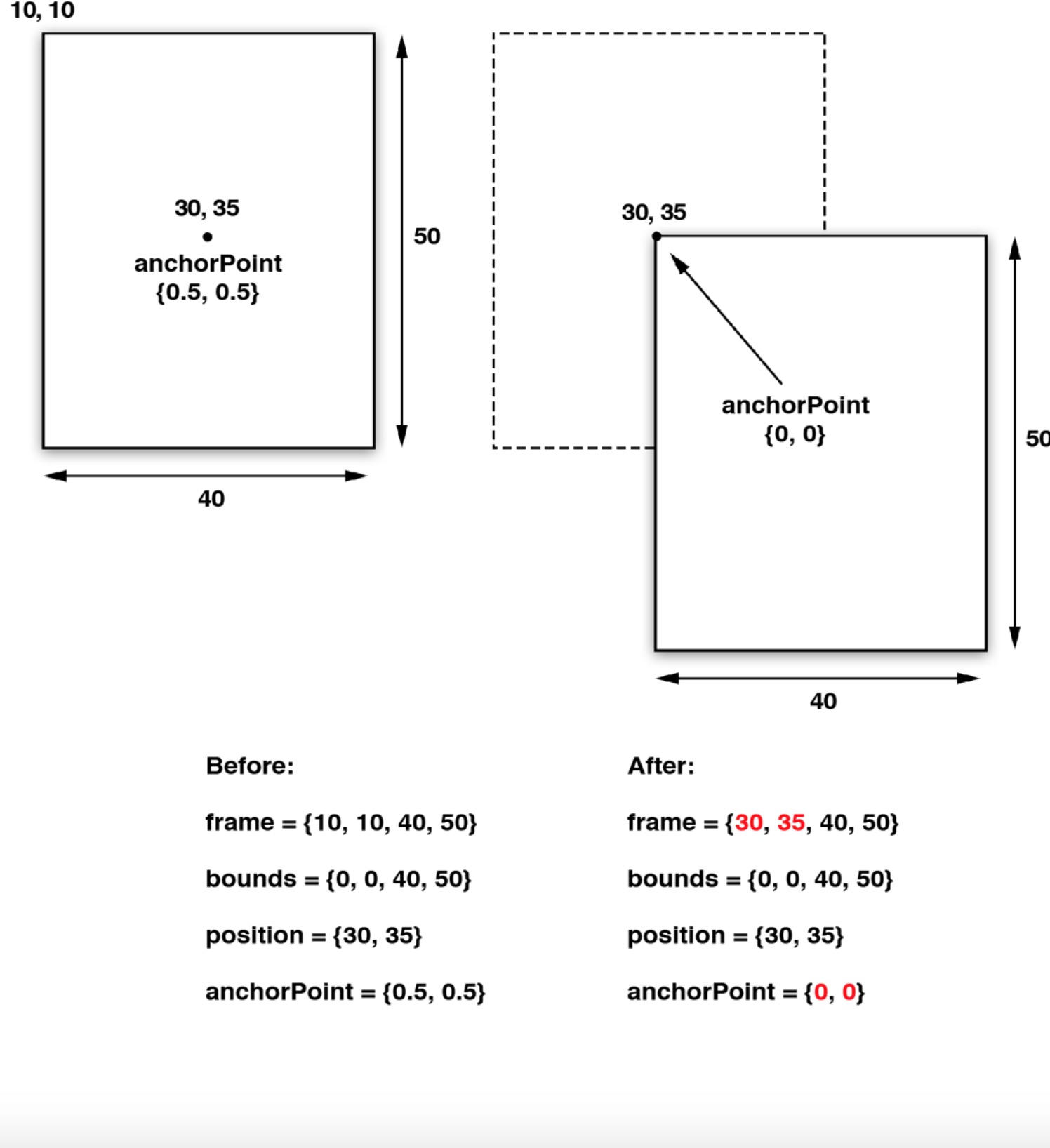
UIView的bounds、frame、center/position、anchorPoint的关系
视图的frame,bounds和center属性仅仅是存取方法,当操纵视图的frame,实际上是在改变位于视图下方CALayer的frame,不能够独立于图层之外改变视图的frame。 对于视图或者图层来说,frame并不是一个非常清晰的属性ÿ…
彻底理解position与anchorPoint
原文 http://www.cnblogs.com/benbenzhu/p/3615516.html 引言 相信初接触到CALayer的人都会遇到以下几个问题: 为什么修改anchorPoint会移动layer的位置? CALayer的position点是哪一点呢? anchorPoint与position有什么关系? 我也迷惑过&…
彻底弄清 anchorPoint 和 position
最近在研读《iOS Core Animation Advanced Techniques》这一本书,想系统地学习下关于 CALayer、Transition、以及动画等知识点。大家可以在 gitbook 上面找到该书的翻译版本。
传送门
在读到图层几何学这一章的时候,了解到了两个概念:anc…
Cocos2dx学习笔记9:cocos2dx锚点(Anchor Point)
锚点(AnchorPoint)是相对坐标,通常用来定义物体内部的点,在cocos2dx中,一般都是以加载精灵来实现游戏元素的表现,而精灵一般都是对应的一张图片资源。 我们在设置精灵位置的时候,要设置精灵中的锚点来和我们的坐标点相…
Anchorpoints学习笔记:
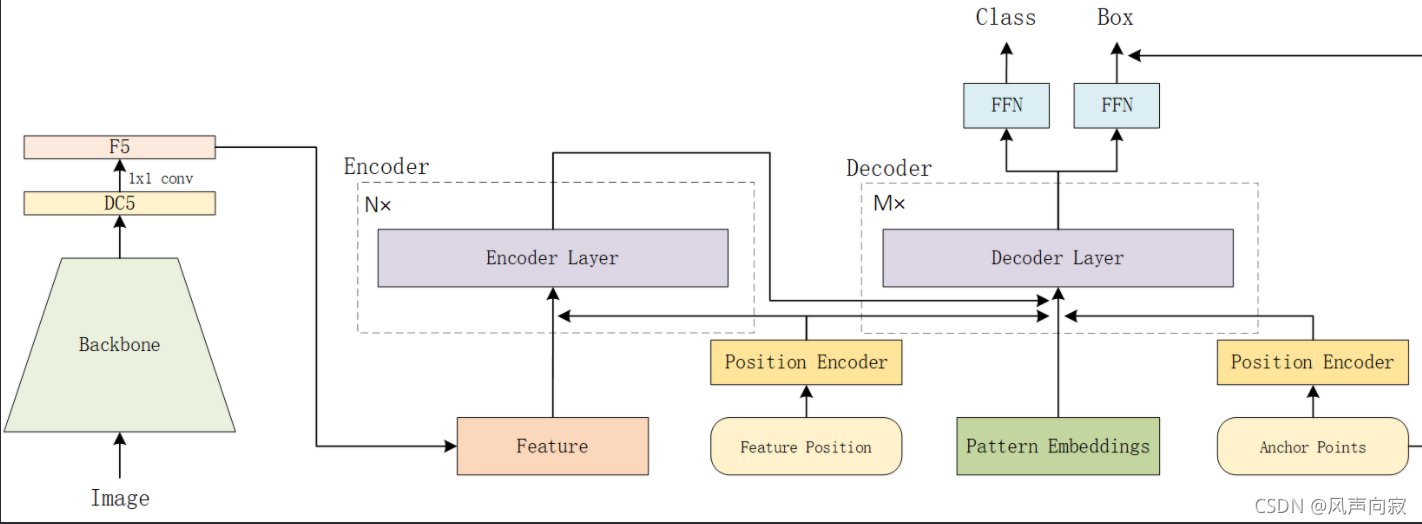
Anchor Detr学习笔记: 文章目录 Anchor Detr学习笔记:1.首先介绍下什么叫锚点(Anchor point)2.再来介绍下什么叫DETR3.Anchor Detr 1.首先介绍下什么叫锚点(Anchor point)
Anchor point就类似一张钉…
数学篇(三)向量的基本运算
1.平面向量
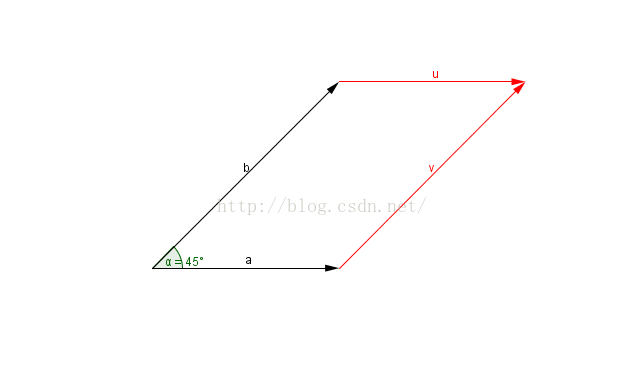
1.1平面向量的加法运算
两个向量,;
向量满足四边形法则; 1.2平面向量的乘法运算
两个向量,;
向量乘表示为
;
相比于向量加运算,向量乘运算要复杂点,很难看明白向量乘的几何意…
2. 数据类型、向量、向量索引、向量修改、向量运算
b站课程视频链接:https://www.bilibili.com/video/BV19x411X7C6?p1 腾讯课堂(最新,但是要花钱,我花99元😢😢买了,感觉不错):https://ke.qq.com/course/3707827#term_id103855009 &a…
matlab 向量的基本运算
本文主要参考:王沫然编著的MATLAB与科学计算(第2版) 博客文章:点击打开链接
1、向量生成 1.1、直接输入 1.2、 xx0:step:xn 1.3、线性等分向量—linespace 1.4、对数等分向量—logspace 2、向量运算 21、加(减&#x…
向量复习(一):定义、求解、四则运算、点积和叉积
向量复习(一) 1. 向量的定义2. 向量的表示3. 向量的求解4. 向量的四则运算4.1 加法4.2 减法4.3 乘法和除法 5. 点积和叉积5.1 点积5.2 叉积 6. 模的求解7. 附录:代码8. 免责声明 首先,我们先来复习一下二维空间几何求交涉及的向量…
两个向量的点乘和叉乘怎么算_数学基础 —— 向量运算:点乘和叉乘
向量的点乘:a * b 公式:a * b |a| * |b| * cosθ 点乘又叫向量的内积、数量积,是一个向量和它在另一个向量上的投影的长度的乘积;是标量。 点乘反映着两个向量的“相似度”,两个向量越“相似”,它们的点乘越大。 向量…
数学基础 —— 向量运算(叉乘)
向量的叉乘,即求同时垂直两个向量的向量,即c垂直于a,同时c垂直于b(a与c的夹角为90,b与c的夹角为90)
c ab (a.y*b.z-b.y*a.z , b.x*a.z-a.x*b.z , a.x*b.y-b.x*a.y) 以上图为例a…
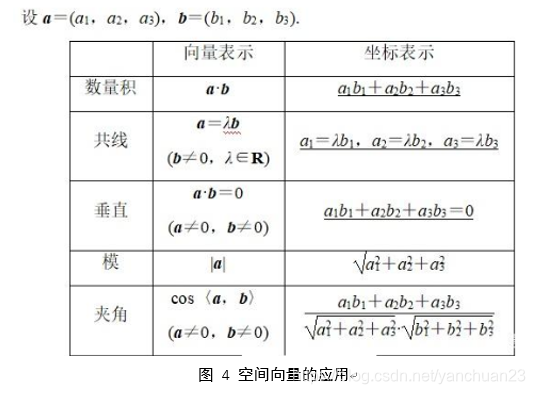
常用的几种向量运算法则
a ⋅ b b ⋅ a ab ba a⋅bb⋅a a ( b ⋅ c ) ≠ ( a ⋅ b ) c a(bc)≠(ab)c a(b⋅c)(a⋅b)c ( a b ) ⋅ c a ⋅ c b ⋅ c (ab)c acbc (ab)⋅ca⋅cb⋅c a b − b a ab - ba ab−ba ( r a ) b a ( r b ) r ( a b ) , 其 中 r 是 标 量 (ra)ba(rb)r(ab),其中r是…
MATLAB——向量的运算
文章目录 一.向量的定义:***向量的生成方法:直接输入法、冒号法和利用MATLAB函数创建三种方法。*** 二.向量元素的引用:三.向量的定义与赋值:四.向量的点积运算:向量的叉积:向量的混合积: 一.向…