原文

引言

相信初接触到CALayer的人都会遇到以下几个问题：  
为什么修改anchorPoint会移动layer的位置？ 
CALayer的position点是哪一点呢? 
anchorPoint与position有什么关系？

我也迷惑过，找过网上的教程，大部分都是复制粘贴的，有些是翻译的文章但很有问题，看得似懂非懂，还是自己写代码彻底弄懂了，做点笔记吧。

每一个UIView内部都默认关联着一个CALayer, UIView有frame、bounds和center三个属性，CALayer也有类似的属性，分别为frame、bounds、position、anchorPoint。frame和bounds比较好理解，bounds可以视为x坐标和y坐标都为0的frame，那position、anchorPoint是什么呢？先看看两者的原型，可知都是CGPoint点。

@property CGPoint position 
@property CGPoint anchorPoint

anchorPoint

一般都是先介绍position，再介绍anchorPoint。我这里反过来，先来说说anchorPoint。

从一个例子开始入手吧，想象一下，把一张A4白纸用图钉订在书桌上，如果订得不是很紧的话，白纸就可以沿顺时针或逆时针方向围绕图钉旋转，这时候图钉就起着支点的作用。我们要解释的anchorPoint就相当于白纸上的图钉，它主要的作用就是用来作为变换的支点，旋转就是一种变换，类似的还有平移、缩放。

继续扩展，很明显，白纸的旋转形态随图钉的位置不同而不同，图钉订在白纸的正中间与左上角时分别造就了两种旋转形态，这是由图钉（anchorPoint）的位置决定的。如何衡量图钉（anchorPoint）在白纸中的位置呢？在iOS中，anchorPoint点的值是用一种相对bounds的比例值来确定的，在白纸的左上角、右下角，anchorPoint分为为(0,0), (1, 1)，也就是说anchorPoint是在单元坐标空间(同时也是左手坐标系)中定义的。类似地，可以得出在白纸的中心点、左下角和右上角的anchorPoint为(0.5,0.5), (0,1), (1,0)。

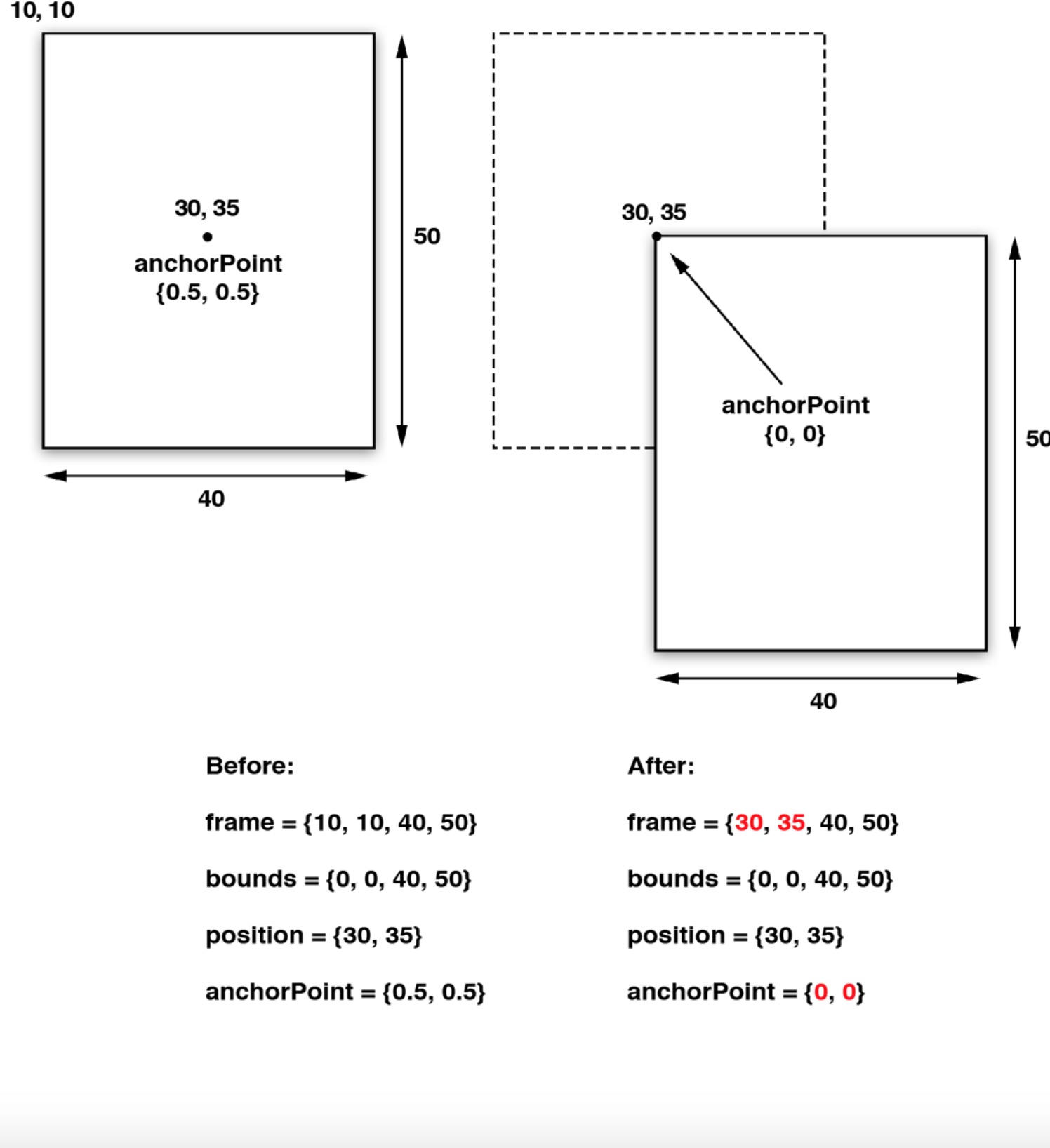
然后再来看下面两张图，注意图中分iOS与MacOS，因为两者的坐标系不相同，iOS使用左手坐标系，坐标原点在左上角，MacOS使用右手坐标系，原点在左下角，我们看iOS部分即可。  

  
图1

  
图2

像UIView有superView与subView的概念一样，CALayer也有superLayer与layer的概念，前面说到的白纸和图中的矩形可以理解为layer，书桌和图中矩形以外的坐标系可以理解成superLayer。如果各自以左上角为原点，则在图中有相对的两个坐标空间。

position

在图1中，anchorPoint有(0.5,0.5)和(0,0)两种情况，分别为矩形的中心点与原点。那么，这两个anchorPoint在superLayer中的实际位置分别为多少呢？简单计算一下就可以得到(100, 100)和(40, 60)，把这两个值分别与各自的position值比较，发现完全一致，该不会是巧合？

这时候可以大胆猜测一下，position是不是就是anchorPoint在superLayer中的位置呢？答案是确定的，更确切地说，position是layer中的anchorPoint点在superLayer中的位置坐标。因此可以说, position点是相对suerLayer的，anchorPoint点是相对layer的，两者是相对不同的坐标空间的一个重合点。

再来看看position的原始定义： The layer’s position in its superlayer’s coordinate space。 
中文可以理解成为position是layer相对superLayer坐标空间的位置，很显然，这里的位置是根据anchorPoint来确定的。

图2中是矩形沿不同的anchorPoint点旋转的形态，这就是类似于刚才讲的图钉订在白纸的正中间与左上角时分别造就了两种旋转形态。

anchorPoint、position、frame

anchorPoint的默认值为(0.5,0.5)，也就是anchorPoint默认在layer的中心点。默认情况下，使用addSublayer函数添加layer时，如果已知layer的frame值，根据上面的结论，那么position的值便可以用下面的公式计算：

1
2

position.x = frame.origin.x + 0.5 * bounds.size.width；  
position.y = frame.origin.y + 0.5 * bounds.size.height；  

里面的0.5是因为anchorPoint取默认值，更通用的公式应该是下面的：

1
2

position.x = frame.origin.x + anchorPoint.x * bounds.size.width；  
position.y = frame.origin.y + anchorPoint.y * bounds.size.height；

下面再来看另外两个问题，如果单方面修改layer的position位置，会对anchorPoint有什么影响呢？修改anchorPoint又如何影响position呢？  
根据代码测试，两者互不影响，受影响的只会是frame.origin，也就是layer坐标原点相对superLayer会有所改变。换句话说，frame.origin由position和anchorPoint共同决定，上面的公式可以变换成下面这样的：

1
2

frame.origin.x = position.x - anchorPoint.x * bounds.size.width；  
frame.origin.y = position.y - anchorPoint.y * bounds.size.height；

这就解释了为什么修改anchorPoint会移动layer，因为position不受影响，只能是frame.origin做相应的改变，因而会移动layer。

理解与运用

在Apple doc对frame的描述中有这么一句话：

Layers have an implicit frame that is a function of the position, bounds, anchorPoint, and transform properties.

可以看到我们推导的公式基本符合这段描述，只不过还缺少了transform，加上transform的话就比较复杂，这里就不展开讲了。

---

Apple doc中还有一句描述是这样的：

When you specify the frame of a layer, position is set relative to the anchor point. When you specify the position of the layer, bounds is set relative to the anchor point.

大意是：当你设置图层的frame属性的时候，position根据锚点（anchorPoint）的值来确定，而当你设置图层的position属性的时候，bounds会根据锚点(anchorPoint)来确定。

这段翻译的上半句根据前面的公式容易理解，后半句可能就有点令人迷惑了，当修改position时，bounds的width与height会随之修改吗？其实,position是点，bounds是矩形，根据锚点(anchorPoint)来确定的只是它们的位置，而不是内部属性。所以，上面这段英文这么翻译就容易理解了：

当你设置图层的frame属性的时候，position点的位置（也就是position坐标）根据锚点（anchorPoint）的值来确定，而当你设置图层的position属性的时候，bounds的位置（也就是frame的orgin坐标）会根据锚点(anchorPoint)来确定。

在实际情况中，可能还有这样一种需求，我需要修改anchorPoint，但又不想要移动layer也就是不想修改frame.origin，那么根据前面的公式，就需要position做相应地修改。简单地推导，可以得到下面的公式：

1
2

positionNew.x = positionOld.x + (anchorPointNew.x - anchorPointOld.x)  * bounds.size.width  
positionNew.y = positionOld.y + (anchorPointNew.y - anchorPointOld.y)  * bounds.size.height

但是在实际使用没必要这么麻烦。修改anchorPoint而不想移动layer，在修改anchorPoint后再重新设置一遍frame就可以达到目的，这时position就会自动进行相应的改变。写成函数就是下面这样的：

1
2
3
4
5

- (void) setAnchorPoint:(CGPoint)anchorpoint forView:(UIView *)view{
  CGRect oldFrame = view;
  view.layer.anchorPoint = anchorpoint;
  view.frame = oldFrame;
}

总结

1、position是layer中的anchorPoint在superLayer中的位置坐标。 
2、互不影响原则：单独修改position与anchorPoint中任何一个属性都不影响另一个属性。 
3、frame、position与anchorPoint有以下关系：

1
2

frame.origin.x = position.x - anchorPoint.x * bounds.size.width；  
frame.origin.y = position.y - anchorPoint.y * bounds.size.height；

第2条的互不影响原则还可以这样理解：position与anchorPoint是处于不同坐标空间中的重合点，修改重合点在一个坐标空间的位置不影响该重合点在另一个坐标空间中的位置。

参考