关于向量

高中数学必修$4$说:

几何向量是线性空间中有大小与方向的量。

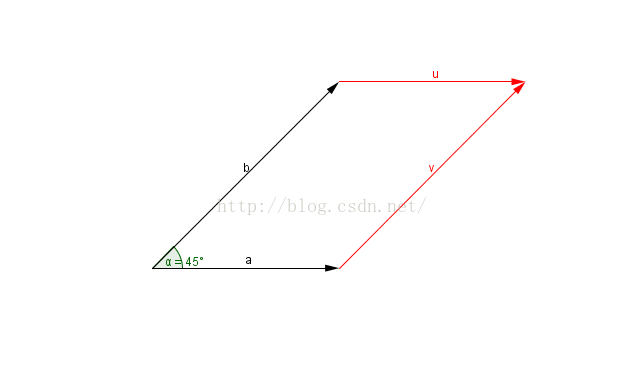
放图理解一下：

如上图所示，向量可以形象的用一根箭头表示。箭头所指代表向量的方向，线段的长度代表向量的大小。

在$OI$中，我们简化了一下向量的存储方式及运算法则，我们定义向量为起点为$(0,0)$的一条有方向的线段。由于我们在考虑向量时只考虑其大小与方向，一般不考虑具体位置，故我们将向量平移至坐标系原点处以简化运算。

所以，在之后的讲解中，我们默认向量和点已经被存在了一个结构体里面（向量和点记录的东西都是一个坐标）：

struct Point{double x,y;  //注意这个double
};

如果想分清楚具体是点还是向量，那么只需要在结构体后加入一句：

typedef Point Vector;

这样我们就可以只开一个结构体而做到存储两种量。

tips:如果您觉得只用Point即可，那么请将后文的Vector全部视为Point（这样写出来也没有任何问题）

向量的运算法则（具体原理请查阅数学必修$4$）

前置：模长

$|A|$表示向量$A$的长度，为一个数。

double Length(const Vector &p){return sqrt(p.x*p.x+p.y*p.y);
}

前置：向量的方向

（请暂且忽略$B$以及$\beta 和\gamma$，后面要用）
我们设向量$A$为$(x,y)$，那么
$$cos(\alpha )=sin(90^{。}-\alpha )=\frac{x}{|A|}$$
$$sin(\alpha )=cos(90^{。}-\alpha )=\frac{y}{|A|}$$
那么，我们定义向量$A$的方向为$w(cos(\alpha ),sin(\alpha ))。$

点±向量=点

//所有的重载运算符都定义在结构体外部，如果不重载运算符的话会很麻烦
Point operator + (const Point &p,const Vector &q){return (Point){p.x+q.x,p.y+q.y};
}
Point operator - (const Point &p,const Vector &q){return (Point){p.x-q.x,p.y-q.y};
}

点-点=向量

Vector operator - (const Point &p,const Point &q){return (Vector){p.x-q.x,p.y-q.y};
}

友情提示：两个减的操作只需要写一个，如果实在看不顺眼，那么就讲其中一个减号改为另外一个不相冲突的符号。

点+点无意义

向量*常数=向量

Vector operator * (const Vector &p,const double &k){//double很重要！！！return (Vector){p.x*k,p.y*k};
}

向量/常数=向量

Vector operator / (const Vector &p,const double &k){return (Vector){p.x/k,p.y/k};
}

向量±向量=向量

代码同点±向量

向量的点积

令向量$X=(x_1,x_2),Y=(y_1,y_2),$则有：

定义式：$X\cdot Y=|X||Y|cos(\gamma )$，其中$\gamma$为$X,Y$的夹角

但更通用的是这样一个式子：$X\cdot Y=|X||Y|cos(\gamma )=x_1{y}_1+x_2{y}_2$

double Dot (const Vector &p,const Vector &q){return p.x*q.x+p.y*q.y;
}

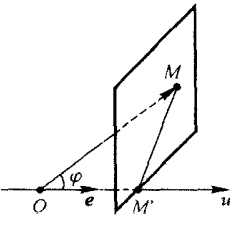
几何意义：A在B所在方向的投影的模长和B的模长的乘积

tips:如果向量$A,B$的点积为$0$，则$A,B$垂直

证明如下：

我们有上面讲到的向量的方向可知，
$$cos(\alpha )=\frac{x_1}{|X|},sin(\alpha )=\frac{x_2}{|Y|}$$
$$cos(\beta )=\frac{y_1}{|X|},sin(\beta )=\frac{y_2}{|Y|}$$
由$\gamma =\alpha -\beta$得：
$$cos(\gamma )=cos(\alpha -\beta )$$
由数学必修4上一个著名公式得：
$$cos(\gamma )=cos(\alpha -\beta )=cos(\beta )cos(\alpha )+sin(\beta )sin(\alpha )$$
$$cos(\gamma )=\frac{x_1}{|X|}\times \frac{y_1}{|Y|}+\frac{x_2}{|X|}\times \frac{y_2}{|Y|}$$
$$cos(\gamma )=\frac{x_1{y}_1+x_2{y}_2}{|X||Y|}$$
$$X\cdot Y=|X||Y|cos(\gamma )=x_1{y}_1+x_2{y}_2$$

向量的叉积

定义式：$X\ast Y=|X||Y|sin(\gamma )$

通用的式子：$X\ast Y=|X||Y|sin(\gamma )=x_1{y}_2-x_2{y}_1$

double Cross (const Vector &p,const Vector &q){return p.x*q.y-q.x*p.y;
}

证明大体同上，需要用到另一个著名的式子：

$$sin(\alpha -\beta )=sin(\alpha )cos(\beta )-cos(\alpha )sin(\beta )$$

几何意义：A转到B所夹平行四边形的有向面积

简单地解释一下：

在$A,B$不共线的情况下，如果$A$在$B$上面，那么它们的叉积就小于$0,$反之则大于$0$。

如果$A,B$共线，那么它们的叉积就等于$0$。

基础运算完整代码

struct Point{double x,y;
};
typedef Point Vector; 
Point operator + (const Point &p,const Vector &q){return (Point){p.x+q.x,p.y+q.y};
}
Vector operator - (const Point &p,const Point &q){return (Vector){p.x-q.x,p.y-q.y};
}
Vector operator * (const Vector &p,const double &k){return (Vector){p.x*k,p.y*k};
}
Vector operator / (const Vector &p,const double &k){return (Vector){p.x/k,p.y/k};
}
double Dot (const Vector &p,const Vector &q){return p.x*q.x+p.y*q.y;
}
double Cross (const Vector &p,const Vector &q){return p.x*q.y-q.x*p.y;
}
double Length(const Vector &p){return sqrt(Dot(p,p));
}