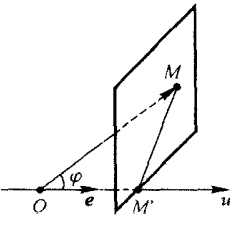
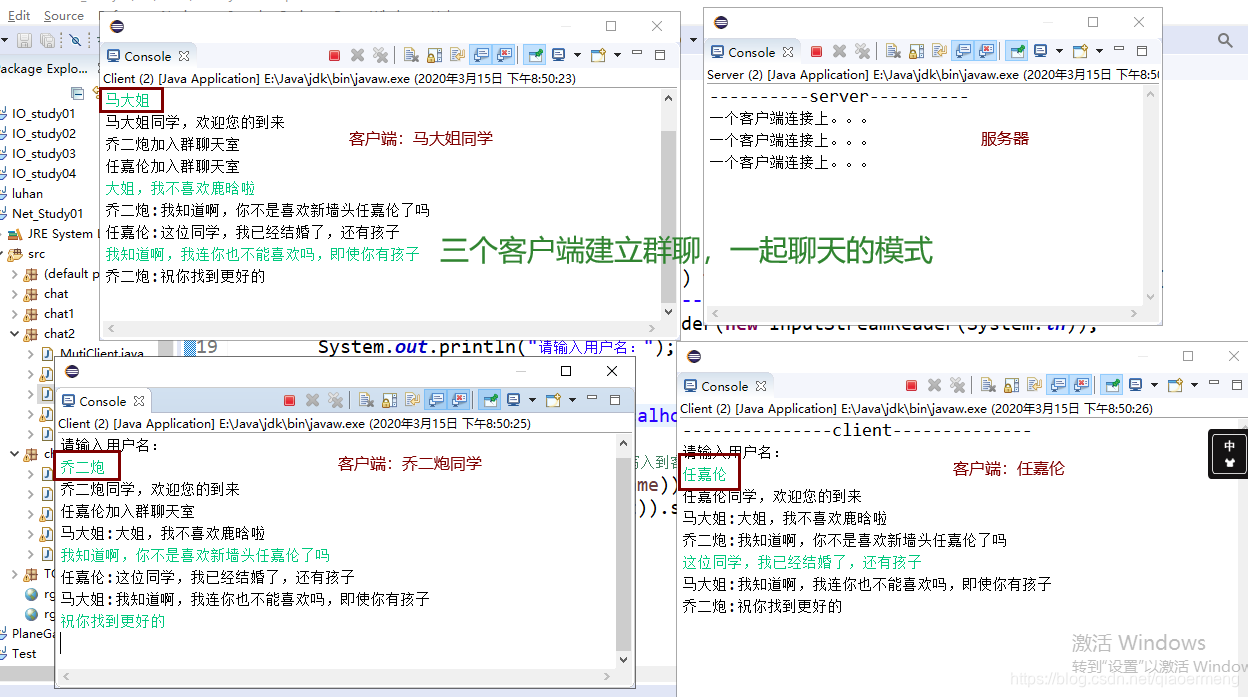
a ⋅ b = b ⋅ a a·b = b·a a⋅b=b⋅a
a ( b ⋅ c ) ≠ ( a ⋅ b ) c a(b·c)≠(a·b)c a(b⋅c)=(a⋅b)c
( a + b ) ⋅ c = a ⋅ c + b ⋅ c (a+b)·c = a·c+b·c (a+b)⋅c=a⋅c+b⋅c
a × b = − b × a a×b = - b×a a×b=−b×a
( r a ) × b = a × ( r b ) = r ( a × b ) , 其 中 r 是 标 量 (ra)×b=a×(rb)=r(a×b),其中r是标量 (ra)×b=a×(rb)=r(a×b),其中r是标量
( a + b ) × c = a × c + b × c (a+b)×c = a×c+b×c (a+b)×c=a×c+b×c
( a × b ) × c = b ( a ⋅ c ) − a ( b ⋅ c ) (a×b)×c = b(a·c) - a(b·c) (a×b)×c=b(a⋅c)−a(b⋅c)
a × ( b × c ) = b ( a ⋅ c ) − c ( a ⋅ b ) a×(b×c) = b(a·c) - c(a·b) a×(b×c)=b(a⋅c)−c(a⋅b)
a × ( b × c ) ≠ ( a × b ) × c a×(b×c) ≠ (a×b)×c a×(b×c)=(a×b)×c
( a × b ) ⋅ ( c × d ) = a ⋅ [ b × ( c × d ) ] (a×b)·(c×d) = a·[b×(c×d)] (a×b)⋅(c×d)=a⋅[b×(c×d)]
a × ( b × c ) + b × ( c × a ) + c × ( a × b ) = 0 a×(b×c)+b×(c×a)+c×(a×b)=0 a×(b×c)+b×(c×a)+c×(a×b)=0
a × ( b × c ) = ( a T c ) b − ( a T b ) c = [ a T c − c a T ] b a×(b×c)=(a^{T}c)b-(a^{T}b)c=[a^{T}c-ca^{T}]b a×(b×c)=(aTc)b−(aTb)c=[aTc−caT]b
a × b = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] [ b 1 b 2 b 3 ] a \times b=\left[\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}\right]\left[\begin{array}{l} b_{1} \\ b_{2} \\ b_{3} \end{array}\right] a×b=⎣⎡0a3−a2−a30a1a2−a10⎦⎤⎣⎡b1b2b3⎦⎤
a × ( b × c ) = [ 0 − a 3 a 2 a 3 0 − a 1 − a 2 a 1 0 ] [ 0 − b 3 b 2 b 3 0 − b 1 − b 2 b 1 0 ] [ c 1 c 2 c 3 ] a \times(b \times c)=\left[\begin{array}{ccc} 0 & -a_{3} & a_{2} \\ a_{3} & 0 & -a_{1} \\ -a_{2} & a_{1} & 0 \end{array}\right]\left[\begin{array}{ccc} 0 & -b_{3} & b_{2} \\ b_{3} & 0 & -b_{1} \\ -b_{2} & b_{1} & 0 \end{array}\right]\left[\begin{array}{c} c_{1} \\ c_{2} \\ c_{3} \end{array}\right] a×(b×c)=⎣⎡0a3−a2−a30a1a2−a10⎦⎤⎣⎡0b3−b2−b30b1b2−b10⎦⎤⎣⎡c1c2c3⎦⎤
- 代数规则
- 反交换律: a × b = − b × a a×b=-b×a a×b=−b×a
- 加法的分配律: a × ( b + c ) = a × b + a × c a×(b+c)=a×b+a×c a×(b+c)=a×b+a×c
- 与标量乘法兼容: ( r a ) × b = a × ( r b ) = r ( a × b ) (ra)×b=a×(rb)=r(a×b) (ra)×b=a×(rb)=r(a×b)
- 不满足结合律,但满足雅可比恒等式: a × ( b × c ) + b × ( c × a ) + c × ( a × b ) = 0 a×(b×c)+b×(c×a)+c×(a×b)=0 a×(b×c)+b×(c×a)+c×(a×b)=0
- 分配律,线性性和雅可比恒等式别表明:具有向量加法和叉积的R3构成了一个李代数。
- 两个非零向量a和b平行,当且仅当a×b=0。
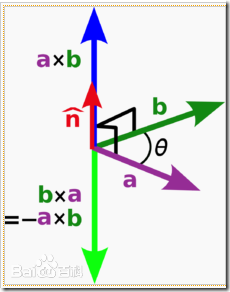
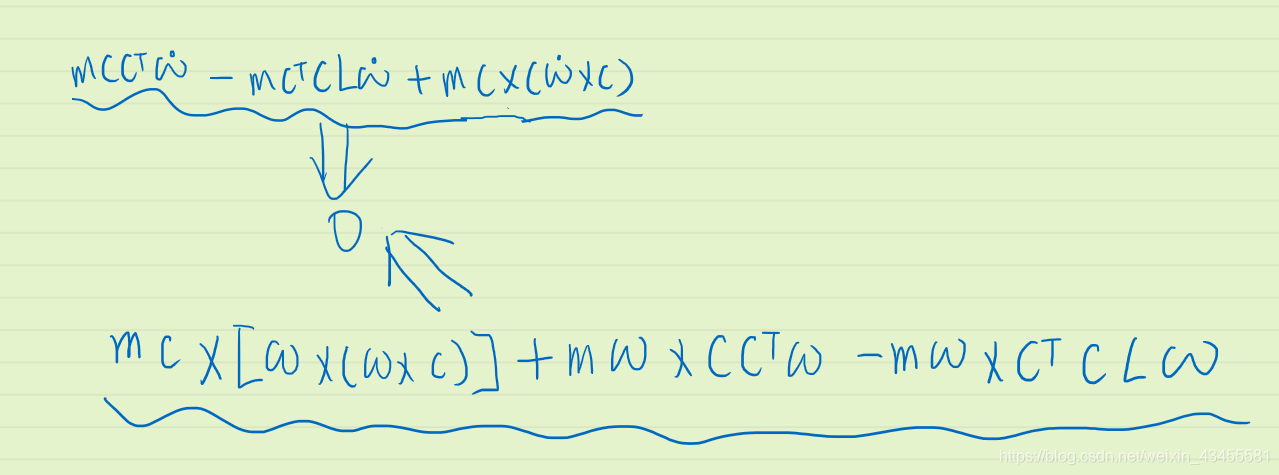
验算:
clear,clc;
syms px py pz wx wy wz real;
c = [px;py;pz]
w = [wx;wy;wz]temp1 = c*c'*w-c'*c*diag([1 1 1])*w+cross(c,cross(w,c))
simplify(temp1)temp2 = cross(c,cross(w,cross(w,c))) + cross(w,c*c'*w)-cross(w,c'*c*diag([1 1 1])*w)
simplify(temp2)