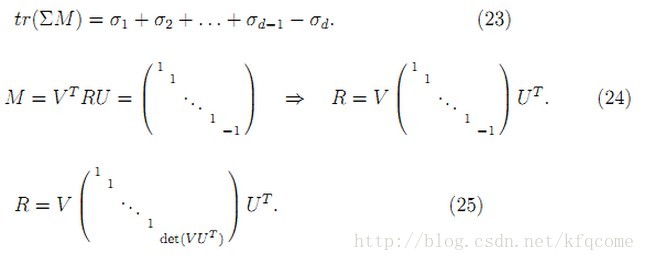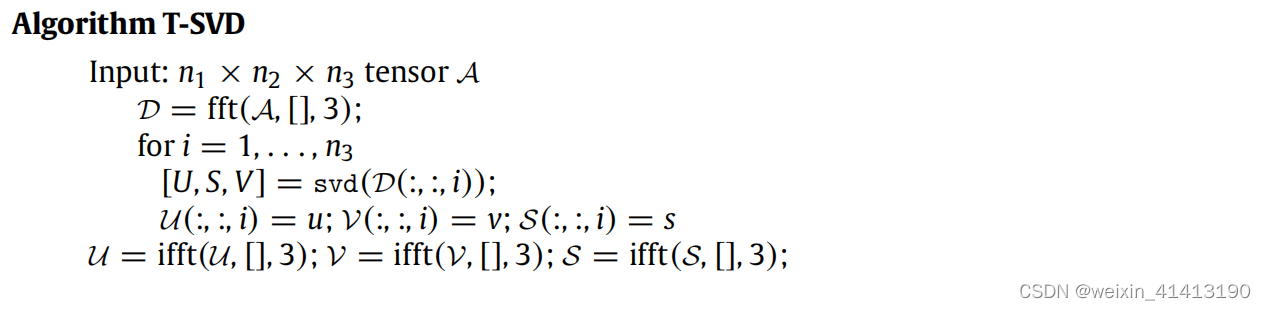转载自《C語言入門學習和書籍推薦》

1、C语言适合当第一门编程语言学习

①、C语言语法相对简单，但又比较完整和严谨，包含该有的各种元素。学完C语言语法，要学习其它编程语言就很容易了。
②、C语言接近底层，可以了解内存和计算机的基本原理。
③、许多基础课程比如算法与数据结构教材都是以C语言为例子的，特别是中国版的书籍。

如果你是大一刚开始学习编程，建议选择C语言做入门。

2、C语言学习的步骤

学习语法和基础算法 —> 了解C语言应用领域 —> 确定是否从事C语言相关工作 —> 深入学习基础课程 —> 学习领域相关的课程

3、C语言语法学习

①、书籍推荐：

推荐《C程序设计语言》和 习题解答

如果上面书籍看不懂，可以选择下面两本之一。

②、学习建议

视频结合书籍，把书籍上的代码都一个个自己敲出来运行，做到每段小程序都熟悉记忆。
不要一直在那边背语法，多写代码，多演化代码，验证语法。
建议以Linux为学习环境，掌握Linux下的相关工具，比如GCC

③、验证结果

《C程序设计语言：习题解答》里面的题目不用看书可以自己敲打实现出来就差不多了。
可以用计算机等级考试二级（C语言）的历年试题验证学习结果。也可以自己报名考看看，以95分做目标。

④、进阶学习

可以先跳过这个，看看是否从事C语言相关工作，如果是的话，再来看这个。

语法进阶书籍推荐：

逻辑思维进阶

南开大学C语言100题，自己实现代码并验证。继续进阶，可以刷OJ

4、C语言应用领域

是不是有些同学学完C语法后都不知道做什么项目。因为单纯学会C语法开发不了什么项目，你需要掌握C语言应用领域，然后学习周边相关知识。

相对于PHP、Java，C语言的开发效率较低，没有框架甚至没有库。数据结构要自己写，对操作系统底层要很熟悉，代码很容易出现内存相关的错误。

C语言主要用于驱动开发、操作系统、内核开发，嵌入式（单片机）、交换机、路由器等网络设备的开发。

如果你想要会用C语言开发项目，就需要掌握相关领域知识。

5、方向选择

学完语法和了解C语言应用领域后，就要面临着选择。三个方向：①、选择从事C语言相关的工作；②、选择继续学习C++，C++主要应用领域游戏服务端开发、图形图像、C/S客户端界面开发、中间件；③、选择其它方向的学习，比如Java

6、深入学习基础课程

选择从事C语言相关的工作，就需要深入学习基础课程。因为从事C语言相关工作，往往对性能有要求，需要理解操作系统和计算机组成原理。

以下课程在从事C语言相关工作是应该要掌握的：
《算法与数据结构》
《计算机组织与体系结构》
《编译原理》
《操作系统原理》

有能力的可以学习《Linux内核结构》

具体每个基础课程的学习就不展开了，以后谈。学习书籍建议，可以参考清华北大计算机系相关课程指定的教程。

7、学习领域相关的课程

这个就比较广泛，根据希望从事的领域有选择性学习。比如，你想从事嵌入式开发，那你就要学习 嵌入式操作系统等

8、项目实践

学完理论，找项目尝试练习。

哪里找项目呢？

①、找培训教程，别人培训班的实践题目或者看网上培训教程的实践题目
②、找高年级或老师帮忙布置实践题目
③、通过Google、GitHub等程序猿社区，去找找实践题目
…

找到题目后，看看自己一个人或者组织几个人能不能搞定。如果搞不定，再根据所缺的知识去补充知识。