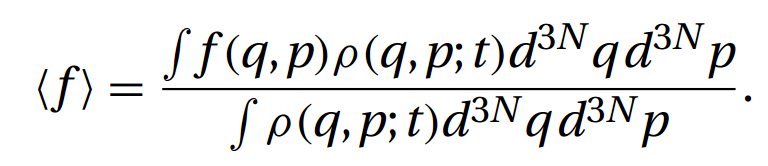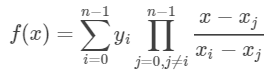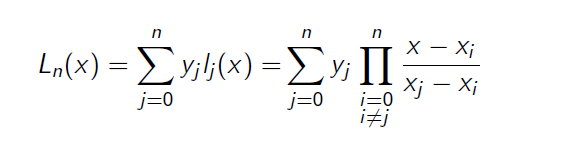更多精彩请关注公众号:分子动力学
一、基 本 介 绍
随着计算机的软硬件和计算技术的发展,利用计算机对物质的微观结构和运动进行数值模拟计算得到了迅速发展,并在此基础上发展了用数值运算统计求和的方法:分子动力学 (MD) 方法和蒙特卡罗(MC) 方法。
这两种方法可以按照原子 (或分子) 的排列和运动的模拟以实现宏观物理量的计算,不仅可以直接模拟物质的宏观特性,得出与实验结果相比拟的计算结果,而且可提供微观结构、粒子运动,有利于从中提取新的概念和理论。
二、历 史 简 述
1957年,Alder和Wainw right首先在硬球模型下,采用经典MD方法研究气体和液体的状态方程,取得了尝试性的成功,由于计算机速度和内存的限制,早期模拟的空间尺度和时间尺度都受到很大的限制。
21世纪80年代后期,由于计算机技术的飞速发展和多体势函数的提出与发展,为分子动力学模拟技术注入了新的活力。
1972年,Lees和Edwards首先将分子动力学模拟应用到了非平衡态的研究,进一步扩展了MD方法的应用范围。
目前,许多在实际实验中无法获得的微观细节,而在分子动力学模拟中可以很方便的得到,这种优点使得分子动力学模拟在新材料的研究和开发、预测材料的介观和宏观性质、生物分子结构与功能预测等领域显得十分重要,由此改变了过去理论计算与实验的关系。
三、模 拟 条 件
1、MD模拟的初始条件
合理的初始位形和初始速度将使得计算系统迅速松弛到所要求的平衡状态,减少计算次数。初始位形和初始速度可通过实验数据、理论模型或两者相结合来确定。
如果模拟系统无固定晶格结构,则每个原子的位置可用舍选法或 Petropolis等方法从初始密度分布得到;
每个原子的初速度可从初始温度分布下的 Maxwell-Bohamann分布来随机选取。对于流体分子系统,粒子的初始速度按高斯分布选取比较合理。
2、周期性边界条件
为了解决用少量的粒子,来模拟宏观体系问题, 引入了周期性边界条件,模拟体系实际上是由基本单元在各个方向上重复叠合而成。但在模拟中只需要保留基本单元,其它单元与基本单元由平移对称性关联。
在处理粒子之间的相互作用时,通常采用“最小影像”约定,就是通过满足不等式条件 rc < L/2来截断位势(rc为截断半径,L是元胞的长)。
3、MD模拟的系综
平衡态分子动力学模拟是在一定的系综下进行 的,常用的平衡系综是NVT和NPT系综,在这两种系综中,涉及到控制温度和压力的技术有调温方法和调压方法。
四、运 动 方 程
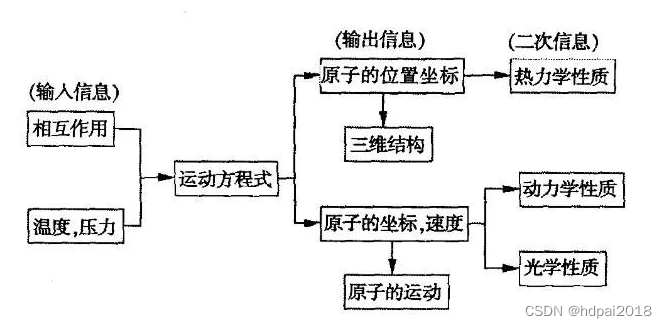
分子动力学模拟的出发点是假定粒子的运动可以用经典动力学来处理,对一个由N个粒子构成的孤立体系,粒子的运动由牛顿运动方程决定,也就是:mid2ri/dt2 =﹣△V (r1,r,2,rn) ,式中,mi、ri分别为第i个原子的质量和位置。
运动方程的数值积分:
计算机模拟方法的基点是利用现代计算机高速和精确的优点,对几百个以至上千个分子的运动方程进行数值积分。
有许多不同的积分方法,它们的效率和方便程度各异,问题基本上就是用有限差分法来对二阶常微分方程进行积分。
常用的有Verlet算法、“蛙跳”(Leap-frog)算法、Velocity-Verlet算法以及Gear的预测-校正算法。
五、 势 函 数
势函数是表示原子间相互作用的函数。势函数的研究和开发是MD发展研究的任务之一。下面按势函数形式介绍一些常用的经典势函数。
1、对势
在MD模拟初期,经常采用对势。对势是仅由两个原子的坐标决定的相互作用,计算两粒子之间的作用力时,不考虑其他粒子影响,比较常见的对势 有:Lennard-Jones势、Morse势以及Johnson势。
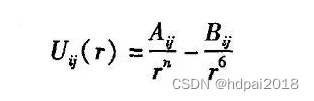
2、多体势
在实际研究中,研究的对象往往是具有较强相互作用的多粒子体系,其中一个粒子状态的变化将会影响其他粒子的变化,不是简单的两两作用,而是多体相互作用。主要包括嵌入原子势(EAM)与MEAM势。
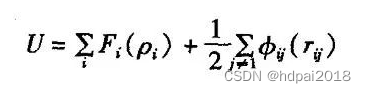
此外,基于EAM势的势函数还有很多种,这些多体势大都用于金属的微观模拟。在MEAM里,镶嵌能项采取了形式F§=AEplnp,其中,E是系数,因不同材料而不同。
原子间势函数的形式多种多样,对于不同的应用对象势参数又互不相同,所以势参数的确定在MD 模拟的应用中至关重要。
势参数的确定通常有三种方法:
一是通过实验值(例如晶格常数、弹性系数等)拟合势参数;
二是通过蒙特卡罗方法确定势参数;
三是通过基于量子力学得到的各种微观信息来确定势参数。
总而言之,经典MD已经得到广泛应用,而原子间 的作用势函数仍然是思考最多的问题,因为势函数对结果精度的影响很大。那么提高势函数的精确性会是将来发展的重点。