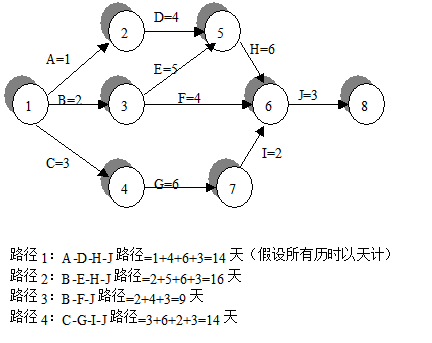
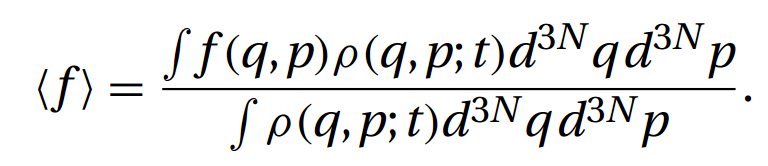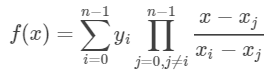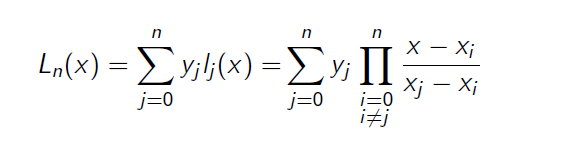- 什么是系综平均?:
下图(来自知乎:卖艺的小青年)中集平均实际就是系综平均,按照随机信号分析的知识来分析,我们可以把这一系列函数看成一个随机信号,取定一个时间,我们就得到一个随机变量,而系综平均实际上就是某一时间点随机变量的期望。(时间平均当然就是某一个样本函数的均值,这里我们不予讨论)。

- 系综平均什么时候和时间平均相等?
首先说明这个问题的意义:
在现实中,我们不可能将一个系统复制无数遍进行试验求集平均,但是我们却可以进行长时间的观察,求出时间平均,这时,如果集平均和时间平均相等,我们就可以简单的将集平均求出。
然后,我们要说明什么是平稳随机过程:
下图(图片来自《随机信号分析(第四版)》作者:李晓峰 周宁 傅志中 李在铭)为严格随机平稳过程的定义,很简单,在我看来,就是概率密度函数不随时间变化,条件严格,更多用于理论研究,一般所说的 平稳性 都是指广义随机平稳。
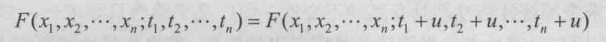
下面是广义平稳随机过程的定义,只要求一二阶的矩具有移动不变性即可,条件较为宽松,更多用于实际研究:
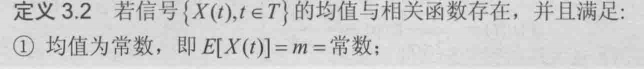

下图给出了广义平稳信号满足均值具有各态历经性的条件,仅仅给出定理,证明请自行查阅。

最后,我们来说明集平均和时间平均相等的条件,只要实信号具有各态历经性,我们就可以说他的集平均和时间平均相等。

- 系综平均系统/集合平均滤波器
在最前面简单介绍以下原理,如果我们有多个添加了噪声的样本信号,而这个信号又具有各态历经性的话,我们完全可以对多个样本进行集合平均,达到滤波的目的。下面我们从信噪比的角度进行分析为什么集合平均可以提高信噪比:
假设我们有n个样本函数,均添加了高斯白噪声,设原本的信号为 S S S,平均功率为 P P P,设添加的高斯白噪声信号分别为 N i , i = 1 , 2 , 3 , . . . n N_i,i=1,2,3,...n Ni,i=1,2,3,...n,白噪声方差为 σ \sigma σ,那么我们可以得到添加了噪声信号的信噪比 L 1 = P σ 2 L_1=\frac{P}{\sigma^2} L1=σ2P(按我的理解,高斯白噪声均值为0,所以可用其方差作为平均功率),我们将各个添加了高斯白噪声的信号相加再除以n,也就是进行集合平均,得到以下公式: L 2 = n P σ 2 L_2=\frac{nP}{\sigma^2} L2=σ2nP(推导仅涉及简单的概率论知识),显然,随着 n n n的增大,信噪比也在增大,这说明集合平均滤波起到了作用。
(1).构建方式:
使用FIFO方式,采多个周期,作为“多个信号”。
原因在于当我们实际滤波时,都是对一个信号进行采样,不太可能取得多个信号进行集合平均, 依据各态历经性,我们可以仅仅使用使用一个周期样本函数的周期相加实现多个样本函数的同时相加(由于笔者目前刚刚开始学习随机信号分析,所以关于各态历经性的说明更偏向于定性的,不准确的说明)
下图引自《Ensemble Averaging Filter for Noise Reduction》
 (下图引自《随机信号分析(第四版)》作者:李晓峰 周宁 傅志中 李在铭)
(下图引自《随机信号分析(第四版)》作者:李晓峰 周宁 傅志中 李在铭)

(2).理论推导:首先以上算法是基于以下算式
y [ n ] = ∑ i = − k k x [ n − k N ] 2 k + 1 k → ∞ y[n]=\frac{\sum_{i=-k}^{k}x[n-kN]}{2k+1}k\rightarrow\infty y[n]=2k+1∑i=−kkx[n−kN]k→∞
即为 y [ n ] = x [ n ] ∗ ∑ i = − k k δ ( n − k N ) 2 k + 1 , k → ∞ y[n]=\frac{x[n]\ast\sum_{i=-k}^{k}\delta(n-kN)}{2k+1},k\rightarrow\infty y[n]=2k+1x[n]∗∑i=−kkδ(n−kN),k→∞
我们对其进行DTFT得到 H ( e j ω ) = 2 π ( 2 k + 1 ) N ∑ i = − ∞ + ∞ δ ( ω − 2 π i N ) , k → ∞ H(e^{j\omega})=\frac{2\pi}{(2k+1)N}\sum_{i=-\infty}^{+\infty}\delta(\omega-\frac{2\pi i}{N}),k\rightarrow\infty H(ejω)=(2k+1)N2π∑i=−∞+∞δ(ω−N2πi),k→∞
对其进行逆DTFT我们得到 h ( n ) = ∑ i = − k k δ [ n − k N ] 2 k + 1 , k → ∞ h(n)=\frac{\sum_{i=-k}^{k}\delta[n-kN]}{2k+1},k\rightarrow\infty h(n)=2k+1∑i=−kkδ[n−kN],k→∞
或者不进行DTFT直接取 y [ n ] = x [ n ] ∗ ∑ i = − k k δ ( ω − k N ) 2 k + 1 , k → ∞ y[n]=\frac{x[n]\ast\sum_{i=-k}^{k}\delta(\omega-kN)}{2k+1},k\rightarrow\infty y[n]=2k+1x[n]∗∑i=−kkδ(ω−kN),k→∞,中的 h [ n ] h[n] h[n]即可。
下面使用matlab对我们的理论分析进行验证。
(3).Matlab代码:
%本代码用于验证ensemble average的滤波效果,输出上分为以下四部分
%1.冲激响应 2.频率响应 3.输入与输出对比
Fs=16384;%采样频率
Perd=100;%输入信号每周期点数,实际上就是N(离散公式中的周期)
Fc=Fs/Perd;%输入信号的频率
Length=2^20;%序列长度
x=1:Length;
S=sin(x*2*pi/Perd);%生成原始信号
S_n=S+0.15*randn(size(x));%生成添加了高斯白噪声的信号
figure('NumberTitle', 'off', 'Name', '生成的带噪声信号');
stem(1:Perd,S_n(1:Perd),'.');
ylim([-1.5 1.5]);%% 以下代码进行集合平均
S_ea=zeros(1,Perd);
for i=1:floor(Length/Perd)S_ea=S_ea+S_n((i-1)*Perd+1:i*Perd);
end
S_ea=S_ea./i;
figure('Name','经集合滤波后的信号');
stem(1:Perd,S_ea(1:Perd),'.');
ylim([-1.5 1.5]);
%% %% 上面的操作实际上就是对输入信号进行了时移,相加,加权,从而有
b=zeros(1,i*Perd);a=i;%传递函数分子分母。
for j=1:ib((j-1)*Perd+1)=1;
end%将b休整为想要的系数
[h1,w1]=freqz(b,a);
figure('Name','集合平均的频响');
plot(w1,abs(h1));
xlabel('\omega/\pi');
set(gca,'XTick',0:pi/4:pi);set(gca,'XTicklabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'})
xlim([0 pi]);
%% 根据多次的结果,可以发现,当Perd逐渐趋于0时,频响函数逐渐在0处逐渐趋于1在其它处逐渐趋于零,这与我们的理论计算相符合。原因在于除0外,其他地方的数值基本都被抵消,这里再提供一种思路,冲激函数串的傅里叶变换仍旧是冲激函数串,可能和这个有关。(k趋于0,周期趋于无穷,从而就在0处有值,别处在无穷远处了。)%% 直接使用Matlab自带的函数impz,就直接处理就行
[h2,w2]=impz(b,a,4000,Fs);%求出单位冲击响应,每个w2对应1/Fs秒
figure('Name','集合平均的单位冲激响应');
stem(w2/Fs,abs(h2),'.');
ylim([0 h2(1)*1.3]);
xlabel('t/s');
% set(gca,'XTick',0:pi/4:pi);set(gca,'XTicklabel',{'0','\pi/4','\pi/2','3\pi/4','\pi'});
%% 可以看到,结果中的冲激是周期的,这与我们预期一致