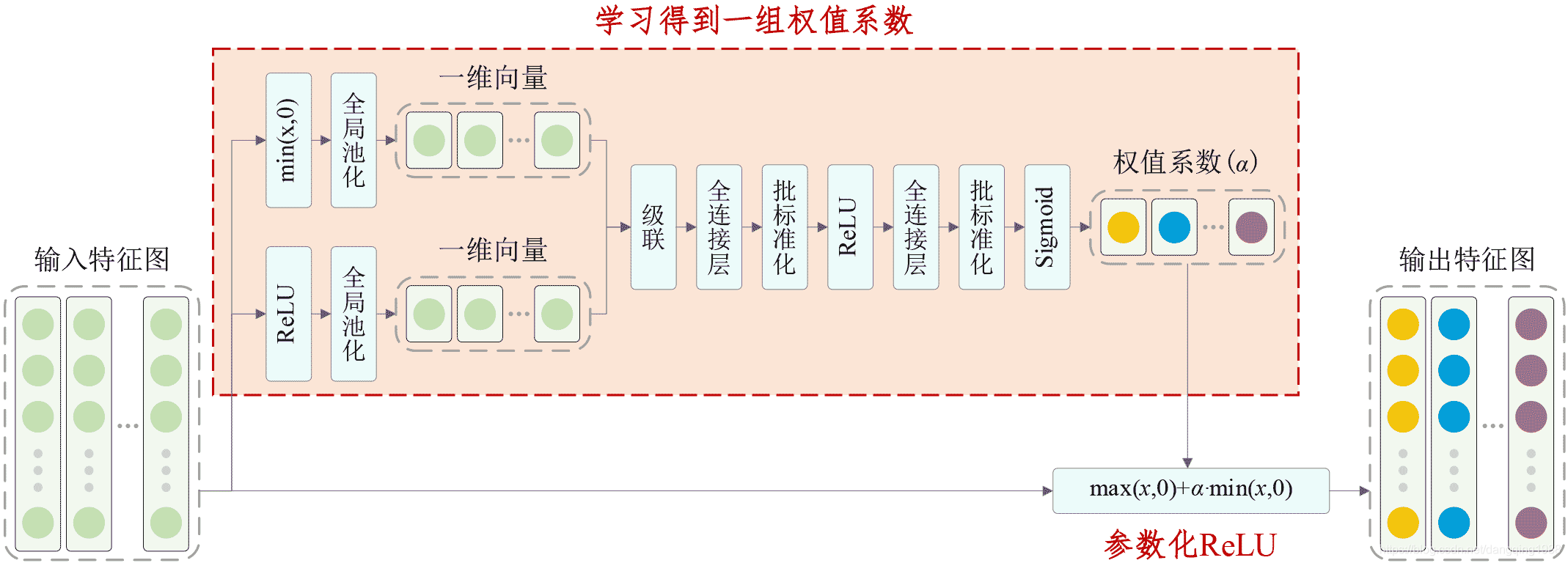
《 N e u r a l n e t w o r k a p p r o a c h t o c o n t i n u o u s − t i m e d i r e c t a d a p t i v e o p t i m a l c o n t r o l f o r p a r t i a l l y u n k n o w n n o n l i n e a r s y s t e m s 》 D r a g u n a V r a b i e ∗ , F r a n k L e w i s {\it《Neural\,network\,approach\,to\,continuous-time\,direct\,adaptive\,optimal\,control\,for\,partially\,unknown\,nonlinear\,systems 》}\\ \qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad\qquad Draguna\,Vrabie*,Frank\,Lewis 《Neuralnetworkapproachtocontinuous−timedirectadaptiveoptimalcontrolforpartiallyunknownnonlinearsystems》DragunaVrabie∗,FrankLewis
非线性最优控制问题:
1. 1.\, 1.最优控制问题描述:
系统动态方程:
x ˙ = f ( x ) + g ( x ( t ) ) u ( x ( t ) ) ; x ( 0 ) = x 0 ( 1 ) \dot{x}=f(x)+g(x(t))u(x(t)) ;\quad x(0)=x_0 \quad(1) x˙=f(x)+g(x(t))u(x(t));x(0)=x0(1)
假设条件: f ( x ) + g ( x ) u f(x)+g(x)u f(x)+g(x)u在包含原点的集合 Ω \Omega Ω上 L i p s c h i t z Lipschitz Lipschitz连续,且系统是可稳的。
定义无限时域积分型性能指标:
V u ( x ( t ) ) = ∫ t ∞ r ( x ( τ ) , u ( τ ) ) d τ , r ( x , u ) = Q ( x ) + u T R u ( 2 ) V^u(x(t))=\int_t^\infty r(x(\tau),u(\tau))d\tau,\quad r(x,u)=Q(x)+u^TRu \quad(2) Vu(x(t))=∫t∞r(x(τ),u(τ))dτ,r(x,u)=Q(x)+uTRu(2)
Q(x)为正定函数,R为正定矩阵。
定义允许控制 μ ∈ Ψ ( Ω ) \mu\in\Psi(\Omega) μ∈Ψ(Ω),满足 μ ( x ) \mu(x) μ(x)在 Ω \Omega Ω上连续, μ ( 0 ) = 0 \mu(0)=0 μ(0)=0, μ ( x ) \mu(x) μ(x) 能使系统稳定,同时 ∀ x 0 ∈ Ω \forall x_0\in \Omega ∀x0∈Ω, V ( x 0 ) V(x_0) V(x0)有限。
对于任意的 μ ∈ Ψ ( Ω ) \mu\in\Psi(\Omega) μ∈Ψ(Ω),其对应的性能指标函数 V μ ( x ( t ) ) = ∫ t ∞ r ( x ( τ ) , u ( τ ) ) d τ ( 3 ) V^\mu(x(t))=\int_t^\infty r(x(\tau),u(\tau))d\tau\quad(3) Vμ(x(t))=∫t∞r(x(τ),u(τ))dτ(3),易知
V μ ( x ) V^\mu(x) Vμ(x)一阶导函数连续,即 V μ ( x ) ∈ C 1 V^\mu(x)\in C^1 Vμ(x)∈C1,故 式 ( 3 ) (3) (3) 微分形式:
0 = r ( x , μ ( x ) ) + ( ∇ V x μ ) T ( f ( x ) + g ( x ) μ ( x ) ) , V μ ( 0 ) = 0 ( 4 ) 0=r(x,\mu(x))+(\nabla V_x^\mu)^T(f(x)+g(x)\mu(x)), \quad V^\mu(0)=0 \quad(4) 0=r(x,μ(x))+(∇Vxμ)T(f(x)+g(x)μ(x)),Vμ(0)=0(4)
最优控制问题 : \textsf{{最优控制问题}}: 最优控制问题:
给 定 连 续 时 间 系 统 ( 1 ) 、 允 许 控 制 集 合 μ ( x ) 、 无 限 时 域 性 能 指 标 V μ ( 2 ) , 找 到 最 优 控 制 律 μ ∗ 使 得 式 ( 2 ) 最 小 \small{给定连续时间系统(1)、允许控制集合\mu(x)、无限时域性能指标V^\mu(2),找到最优控制律\mu^*使得式(2)最小} 给定连续时间系统(1)、允许控制集合μ(x)、无限时域性能指标Vμ(2),找到最优控制律μ∗使得式(2)最小。
2. 2.\, 2.策略迭代算法(policy iteration):
1. 策 略 评 估 ( p o l i c y e v a l u a t i o n ) 1.策略评估(policy\,evaluation) 1.策略评估(policyevaluation)
V μ ( i ) ( x ( t ) ) = ∫ t t + T r ( x ( τ ) , μ ( i ) ( x ( τ ) ) ) d τ + V μ ( i ) ( x ( t + T ) ) , V μ ( i ) ( 0 ) = 0 ( 9 ) V^{\mu^{(i)}}(x(t))=\int_t^{t+T}r(x(\tau),\mu^{(i)}(x(\tau)))d\tau+V^{\mu^{(i)}}(x(t+T)), \, V^{\mu^{(i)}}(0)=0 \quad (9) Vμ(i)(x(t))=∫tt+Tr(x(τ),μ(i)(x(τ)))dτ+Vμ(i)(x(t+T)),Vμ(i)(0)=0(9)
2. 策 略 改 进 ( p o l i c y i m p r o v e m e n t ) 2.策略改进(policy\,improvement) 2.策略改进(policyimprovement)
μ ( i + 1 ) ( x ) = − 1 2 R − 1 g T ( x ) ∇ V x μ ( i ) ( 11 ) \mu^{(i+1)}(x)=-\frac12R^{-1}g^T(x)\nabla V_x^{\mu^{(i)}} \quad(11) μ(i+1)(x)=−21R−1gT(x)∇Vxμ(i)(11)
\,
L e m m a 1. 式 ( 9 ) 求 解 V μ ( i ) 等 价 于 求 解 0 = r ( x , μ ( i ) ( x ) ) + ( ∇ V x μ ( i ) ) T ( f ( x ) + g ( x ) μ ( i ) ( x ) ) , V μ ( i ) ( 0 ) = 0 ( 12 ) Lemma\,1.\;式(9)求解V^{\mu^{(i)}}等价于求解\,0=r(x,\mu^{(i)}(x))+(\nabla V_x^{\mu^{(i)}})^T(f(x)+g(x)\mu^{(i)}(x)), \quad V^{\mu^{(i)}}(0)=0 \quad(12) Lemma1.式(9)求解Vμ(i)等价于求解0=r(x,μ(i)(x))+(∇Vxμ(i))T(f(x)+g(x)μ(i)(x)),Vμ(i)(0)=0(12)
3. 3.\, 3.基于神经网络 近似 指标函数:
V μ ( i ) ( x ) = ∑ j = 1 L w j μ ( i ) ϕ j ( x ) = ( ω L μ ( i ) ) T φ ( x ) ( 14 ) V^{\mu^{(i)}}(x)=\sum_{j=1}^Lw_j^{\mu^{(i)}}\phi_j(x)=(\omega_L^{\mu^{(i)}})^T\varphi(x) \quad (14) Vμ(i)(x)=∑j=1Lwjμ(i)ϕj(x)=(ωLμ(i))Tφ(x)(14)
带入式(9)有:
( ω L μ ( i ) ) T φ ( x ( t ) ) = ∫ t t + T r ( x ( τ ) , μ ( i ) ( x ( τ ) ) ) d τ + ( ω L μ ( i ) ) T φ ( x ( t + T ) ) ( 16 ) (\omega_L^{\mu^{(i)}})^T\varphi(x(t))=\int_t^{t+T}r(x(\tau),\mu^{(i)}(x(\tau)))d\tau+(\omega_L^{\mu^{(i)}})^T\varphi(x(t+T)) \quad (16) (ωLμ(i))Tφ(x(t))=∫tt+Tr(x(τ),μ(i)(x(τ)))dτ+(ωLμ(i))Tφ(x(t+T))(16)
残差为:
δ L μ ( i ) ( x ( t ) , T ) = ∫ t t + T r ( x , μ ( i ) ( x ) ) d τ + ( ω L μ ( i ) ) T [ φ L ( x ( t + T ) ) − φ L ( x ( t ) ) ] ( 17 ) \delta_L^{\mu^{(i)}}(x(t),T)=\int_t^{t+T} r(x,\mu^{(i)}(x))d\tau+(\omega_L^{\mu^{(i)}})^T[\varphi_L(x(t+T))-\varphi_L(x(t))] \quad(17) δLμ(i)(x(t),T)=∫tt+Tr(x,μ(i)(x))dτ+(ωLμ(i))T[φL(x(t+T))−φL(x(t))](17)
使用最小二乘法,最小化 S = ∫ Ω δ L μ ( i ) ( x , T ) δ L μ ( i ) ( x , T ) d x ( 18 ) S=\int_\Omega\delta_L^{\mu^{(i)}}(x,T)\delta_L^{\mu^{(i)}}(x,T)dx \quad(18) S=∫ΩδLμ(i)(x,T)δLμ(i)(x,T)dx(18)
即 ∫ Ω δ L μ ( i ) ( x , T ) d ω L μ ( i ) δ L μ ( i ) ( x , T ) d x = 0 \int_\Omega\frac{\delta_L^{\mu^{(i)}}(x,T)}{d\omega_L^{\mu^{(i)}}}\delta_L^{\mu^{(i)}}(x,T)dx=0 ∫ΩdωLμ(i)δLμ(i)(x,T)δLμ(i)(x,T)dx=0
写成 L e b e s g u e Lebesgue Lebesgue积分的內积形式为:
⟨ δ L μ ( i ) ( x , T ) d ω L μ ( i ) , δ L μ ( i ) ( x , T ) ⟩ Ω = 0 ( 19 ) \langle\frac{\delta_L^{\mu^{(i)}}(x,T)}{d\omega_L^{\mu^{(i)}}},\delta_L^{\mu^{(i)}}(x,T)\rangle_\Omega=0\quad(19) ⟨dωLμ(i)δLμ(i)(x,T),δLμ(i)(x,T)⟩Ω=0(19)
结合 式(17) 和 式(19) 有:
⟨ [ φ L ( x ( t + T ) ) − φ L ( x ( t ) ) ] , [ φ L ( x ( t + T ) ) − φ L ( x ( t ) ) ] ⟩ Ω ω L μ ( i ) + ⟨ [ φ L ( x ( t + T ) ) − φ L ( x ( t ) ) ] , ∫ t t + T r ( x , μ ( i ) ( x ) ) d τ ⟩ Ω = 0 ( 20 ) \begin{aligned} &\langle[\varphi_L(x(t+T))-\varphi_L(x(t))],[\varphi_L(x(t+T))-\varphi_L(x(t))]\rangle_\Omega\omega_L^{\mu^{(i)}}\\ &+\langle[\varphi_L(x(t+T))-\varphi_L(x(t))],\int_t^{t+T} r(x,\mu^{(i)}(x))d\tau\rangle_\Omega=0\quad(20) \end{aligned} ⟨[φL(x(t+T))−φL(x(t))],[φL(x(t+T))−φL(x(t))]⟩ΩωLμ(i)+⟨[φL(x(t+T))−φL(x(t))],∫tt+Tr(x,μ(i)(x))dτ⟩Ω=0(20)
假设 Φ = ⟨ [ φ L ( x ( t + T ) ) − φ L ( x ( t ) ) ] , [ φ L ( x ( t + T ) ) − φ L ( x ( t ) ) ] ⟩ Ω \Phi=\langle[\varphi_L(x(t+T))-\varphi_L(x(t))],[\varphi_L(x(t+T))-\varphi_L(x(t))]\rangle_\Omega Φ=⟨[φL(x(t+T))−φL(x(t))],[φL(x(t+T))−φL(x(t))]⟩Ω可逆,有:
ω L μ ( i ) = − Φ − 1 ⟨ [ φ L ( x ( t + T ) ) − φ L ( x ( t ) ) ] , ∫ t t + T r ( x , μ ( i ) ( x ) ) d τ ⟩ Ω ( 21 ) \omega_L^{\mu^{(i)}}=-\Phi^{-1}\langle[\varphi_L(x(t+T))-\varphi_L(x(t))],\int_t^{t+T} r(x,\mu^{(i)}(x))d\tau\rangle_\Omega\quad(21) ωLμ(i)=−Φ−1⟨[φL(x(t+T))−φL(x(t))],∫tt+Tr(x,μ(i)(x))dτ⟩Ω(21)
4. 4.\, 4.基于Actor/Critic的在线算法:
算法结构:

算法流程图:

示例1:
考虑如下动态系统:
{ x ˙ 1 = − x 1 + x 2 x ˙ 2 = f ( x ) + g ( x ) u \left\{\begin{aligned} &\dot{x} _1= -x_1+x_2\\ &\dot{x} _2= f(x)+g(x)u \end{aligned}\right. {x˙1=−x1+x2x˙2=f(x)+g(x)u
其中, f ( x ) = − 1 2 ( x 1 + x 2 ) + 1 2 x 2 sin ( x 1 ) g ( x ) = sin ( x 1 ) f(x)= -\frac12(x_1+x_2)+\frac12x_2\sin(x_1)\quad g(x)=\sin(x_1) f(x)=−21(x1+x2)+21x2sin(x1)g(x)=sin(x1)
定义无限时域性能指标函数 V u ( x ( t ) ) = ∫ t ∞ ( Q ( x ) + u 2 ) d τ V^u(x(t))=\int_t^\infty(Q(x)+u^2)d\tau Vu(x(t))=∫t∞(Q(x)+u2)dτ, Q ( x ) = x 1 2 + x 2 2 Q(x)=x_1^2+x_2^2 Q(x)=x12+x22
对 ∀ x ∈ Ω \forall x\in\Omega ∀x∈Ω, V μ ( i ) ( x ) V^{\mu^{(i)}}(x) Vμ(i)(x) 由如下光滑函数近似:
V L μ ( i ) ( x ) = ( ω L μ ( i ) ) T φ ( x ) V_L^{\mu^{(i)}}(x)=(\omega_L^{\mu^{(i)}})^T\varphi(x) VLμ(i)(x)=(ωLμ(i))Tφ(x) , L = 3 L=3 L=3
ω 3 μ ( i ) = [ w 1 μ ( i ) w 2 μ ( i ) w 3 μ ( i ) ] T \omega_3^{\mu^{(i)}}=[w_1^{\mu^{(i)}}\,w_2^{\mu^{(i)}}\,w_3^{\mu^{(i)}}]^T ω3μ(i)=[w1μ(i)w2μ(i)w3μ(i)]T, φ 3 ( x ) = [ x 1 2 x 1 x 2 x 2 2 ] T \varphi_3(x)=[x_1^2\,\,x_1x_2\,\,x_2^2]^T φ3(x)=[x12x1x2x22]T
根据式(21)更新权重w。
matlab代码如下:
function odestart
clear all;close all;clc;global P; %w权重
global Target; %cost积分
global v;figure;hold on;%initializations
%iteration step
j=0;
%initial state
x0=[1 1 0];
% P gives the controller parameters
P=[-1 3 1.5];Target=0;
vv=[];
C=[];T=0.1; %采样间隔
Fsamples=150; %采样总点数
nop=30; %一次更新采样点数%next WW gives the initial stabilizing controller
WW=zeros(length(P),1+Fsamples/nop); %记录w权重
WW(:,1)=P'; for k=1:Fsamplesj=j+1;% simulation of the system to get the measurementstspan=[0 T];[t,x]= ode23(@odefile,tspan,x0);x1=x(length(x),(1:2));X(j,:)=[x0(1)^2 x0(1)*x0(2) x0(2)^2]'- [x1(1)^2 x1(1)*x1(2) x1(2)^2]';Target=x(length(x),3);Y(j,:)=Target;%每次更新w,随机五次初始状态,即采样五条状态轨迹if mod(k,nop/5)==0x0=[2*(rand(1,2)-1/2) 0];elsex0=[x1 0];endplot(t+T*(k-1),x(:,1));vv=[vv v]; %记录控制量%每次更新w,采样nop个点if mod(k,nop)==0weights=X\Y;%calculating the matrix PP=[weights(1) weights(2) weights(3)];WW(:,k/nop+1)=[weights(1) weights(2) weights(3)]';X=zeros(nop,3);Y=zeros(nop,1);j=0;x0=[0.5*(rand(1,2)-1/2) 0];endend
P=[weights(1) weights(2) weights(3)]title('System states'); xlabel('Time (s)');figure; plot([0:T:T*(length(vv)-1)],vv); title('Control signal'); xlabel('Time (s)')figure; % in this figure we plot the neural network parameters at each iteration step in the policy iteration
WW % the matrix of parameteres is printed in the comand window
ss=size(WW);
plot((0:T*nop:T*Fsamples),WW(1,1:ss(2))','.-');hold on
plot((0:T*nop:T*Fsamples),WW(2,1:ss(2))','*:'); hold on
plot((0:T*nop:T*Fsamples),WW(3,1:ss(2))','o--');
legend('w_1','w_2 ','w_3');
title('W parameters'); xlabel('Time (s)'); %hold on; plot(T*(Fsamples+1),WW(:,length(WW))','*'); title('W parameters');%-------------------------------------------------------------------------------------
function xdot=odefile(t,x);
global P;
global v;Q=[1 0; 0 1];R=1;
x=[x(1) x(2)]';%calculating the control signal
% P are the parameters of the critic
v=-1/2*inv(R)*sin(x(1))*P*[0; x(1); 2*x(2)];%xdot=[A*[x1;x2;x3;x4]+B*v %+F*deltaPd
xdot=[[-1 1; -1/2 -1/2]*x+[0; 1/2*x(2)*(sin(x(1))^2)+sin(x(1))*v]; x'*Q*x+v'*R*v];
%-------------------------------------------------------------------------------------
运行结果: