堆排序中用到了建立大小堆和向下调整的内容,对这些内容有些不了解的同学可以去补一补专门写堆的博客,方便更好的理解堆排序数据结构之堆(Heap),堆的相关操作,用堆模拟优先级队列。
如果把待排序序列分为未排序区间和有序区间,堆排序大的思想是每次选一个数放到有序区间,没经历一个循环有序区间就会加一,无序区间减一,循环结束序列也就有序了,像这样:
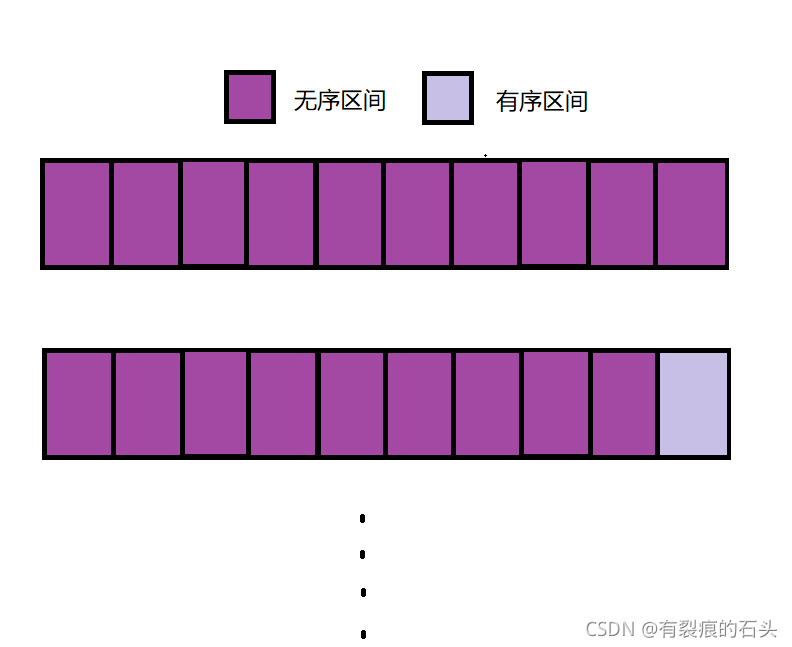
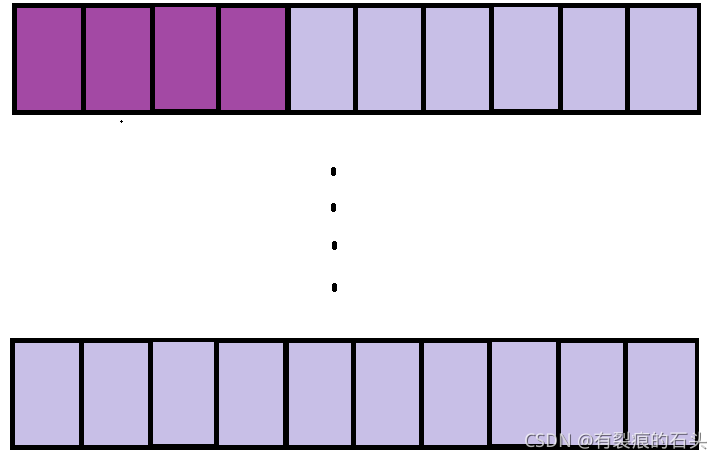
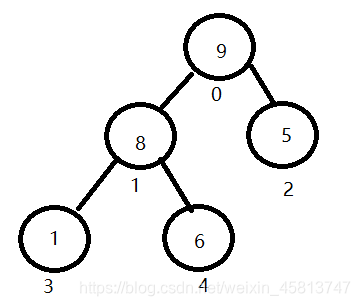
可以发现堆排序的思路和选择排序很像,没错,思路确实一样,只不过选择排序每次要遍历无序区间去找当前无序区间的最大值(升序找最大值,降序找最小值),而堆排序呢是吧无序区间看做一个堆,堆顶自然是这个堆的最值了,每次循环只需要将堆顶元素取出来和无序区间最后一个数交换以达到有序区间加一的目的,然后在对这个堆(注意此时堆的size减一)向下调整,这样做之后下次循环继续取堆顶元素和无序区间最后一个元素交换然后继续循环。。。。。。直到无序区间就剩一个元素,此时整个序列就有序了。下面是图解(图中无序区间是堆,右下角红色是有序区间注意观察):

好了知道了原理之后我们来介绍具体实现。
对于堆排序在实现的时候要知道:
- 待排序序列需要升序排列那么要建大堆
- 待排序序列需要降序排列那么要建小堆
为什么要有上面的两条规定呢?要升序排列就不能建小堆,要降序排列就不能建大堆吗?这个问题大家先自己思考一下,我们先讨论代码实现之后在对这个问题进行讨论:
升序大堆
//建大堆升序public static void heapSort1(int[] array){createHeap1(array);for (int i = 1; i < array.length; i++){int t = array[0];int lastIndex = array.length - i;array[0] = array[lastIndex];array[lastIndex] = t;shiftDown1(array, lastIndex, 0);}}//建大堆public static void createHeap1(int[] array){int size = array.length;int parent = (size - 2) / 2;for (int i = parent; i >= 0; i--){shiftDown1(array, size, i);}}//大堆向下调整public static void shiftDown1(int[] array, int size, int index){while (true){int leftChild = index * 2 + 1;if (leftChild >= size){return;}int rightChild = leftChild + 1;int bigIndex = leftChild;int bigVal = array[leftChild];if (rightChild < size && array[rightChild] > bigVal){bigIndex = rightChild;bigVal = array[rightChild];}if (array[index] >= bigVal){return;}array[bigIndex] = array[index];array[index] = bigVal;index = bigIndex;}}
降序小堆:
//降序建小堆public static void heapSort2(int[] array){createHeap2(array);for (int i = 1; i < array.length; i++){int lastIndex = array.length - i;int t = array[0];array[0] = array[lastIndex];array[lastIndex] = t;shiftDown2(array, lastIndex, 0);}}//建小堆public static void createHeap2(int[] array){int size = array.length;int parent = (size - 2) / 2;for (int i = parent; i >= 0; i--){shiftDown2(array, size, i);}}//小堆向下调整public static void shiftDown2(int[] array, int size, int index){while (true){int leftChild = index * 2 + 1;if (leftChild >= size){return;}int rightChild = leftChild + 1;int minIndex = leftChild;int minVal = array[minIndex];if (rightChild < size && array[rightChild] < minVal){minIndex = rightChild;minVal = array[rightChild];}if (array[index] <= minVal){return;}array[minIndex] = array[index];array[index] = minVal;index = minIndex;}}
同学们不要看见两大篇代码就烦哈,其实代码基本一样就是在个别地方有了调整,看懂一个第二个很容易就能明白。
最后我们来讨论刚才的问题:
为什么要有上面的两条规定呢?要升序排列就不能建小堆,要降序排列就不能建大堆吗?
答案是可以,但是不推荐,请看下图:
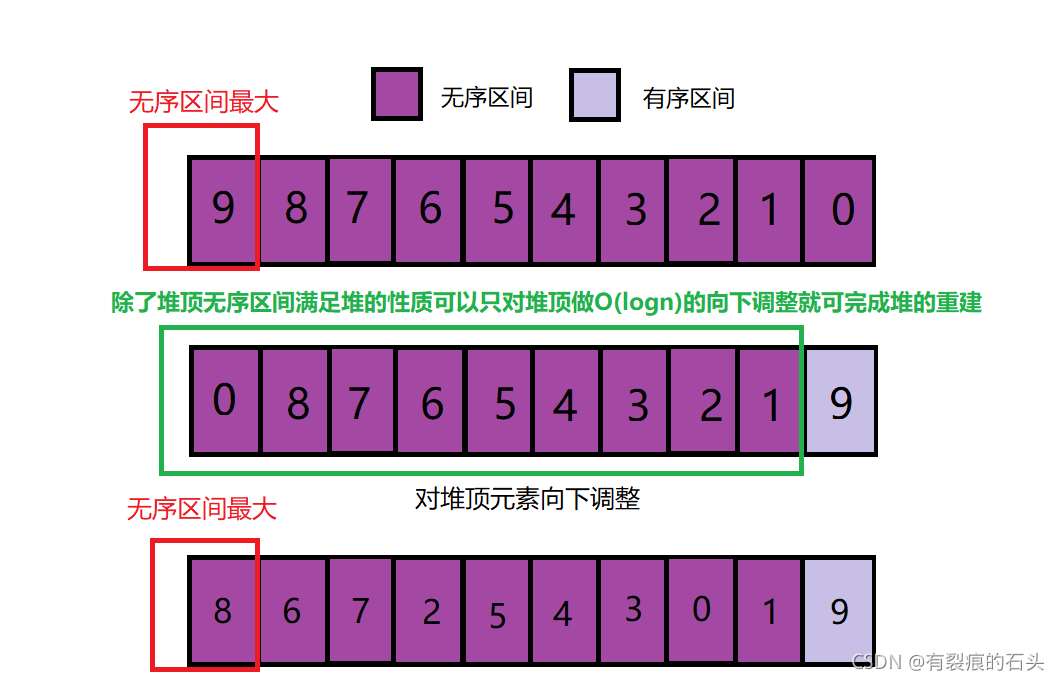
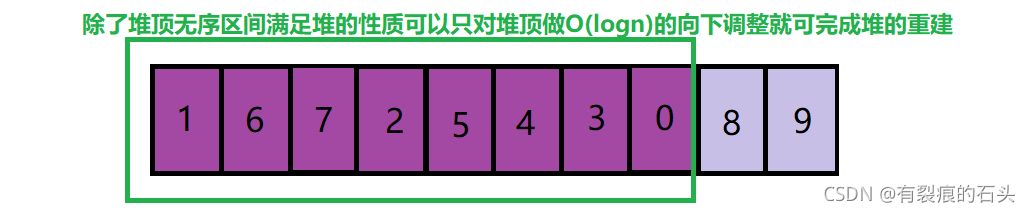
相反如果要通过建小堆完成让数组升序排列的话,因为小堆堆顶元素是最小值,而堆顶这个位置也是排序之后最小值的位置就是说堆顶元素不用在移动了,那么我们的堆要从后面一位重新建立,在建立一个小堆,找出最小值,在往后面一位找出最小值直到整个数组成升序排列,乍一看好像没有问题,但是和建大堆不同的是建小堆每次都要从下一位重新建堆才能选出最值,这个操作的复杂度为O(nlogn),要比建大堆每次只用将堆顶元素向下调整的时间复杂度为O(logn)满很多,所以虽然可以升序建小堆但是因为相对没有建大堆速度快所以我们选择建大堆。
对应的降序建小堆也是同理。