【转载】梯度下降算法的参数更新公式

article/2025/7/22 6:10:57

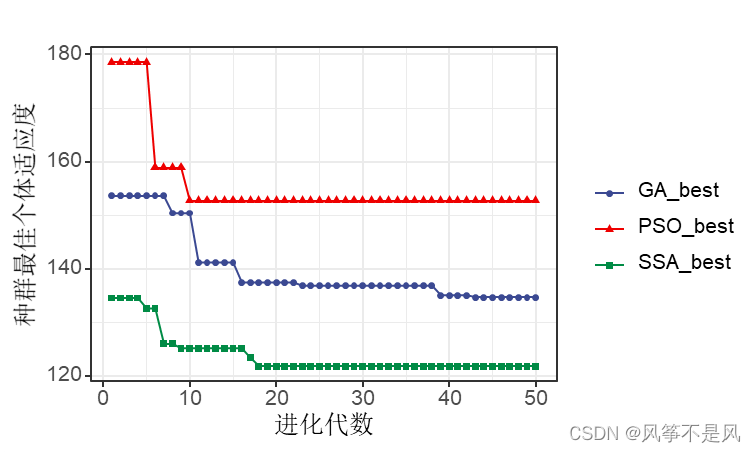
NN这块的公式，前馈网络是矩阵乘法。损失函数的定义也是一定的。

但是如何更新参数看了不少描述，下面的叙述比较易懂的：

1、在吴恩达的CS229的讲义的第四页直接给出参数迭代公式

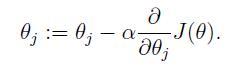
在UFLDL中反向传导算法一节也是直接给出的公式

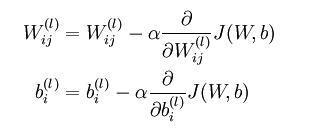
2、例子：

第一步：随机对比重（a,b）赋值并计算误差平方和（SSE）

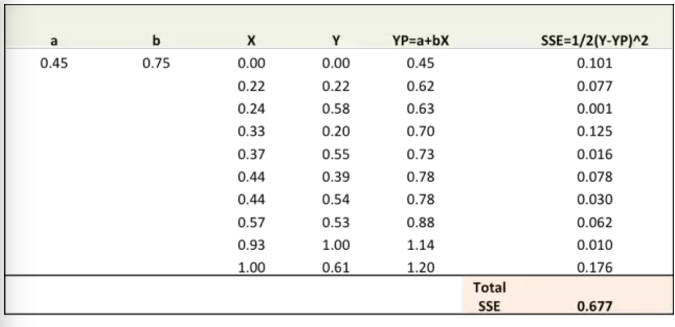
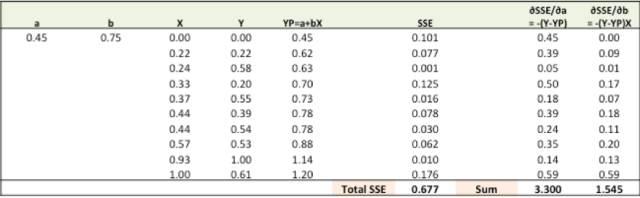
第二步：通过对误差比重（a,b）求导计算出误差梯度（注：YP即Ypred）

∂SSE/∂a = – (Y-YP)

∂SSE/∂b = – (Y-YP)X

误差公式：SSE=½ (Y-YP)^2 = ½(Y-(a+bX))^2

这里涉及到一些微积分，不过仅此而已。∂SSE/∂a 和 ∂SSE/∂b 就被称之为梯度，他们代表a,b相对SSE移动的方向。

第三步：通过梯度调整a,b，使得a,b最佳即所得SSE最小

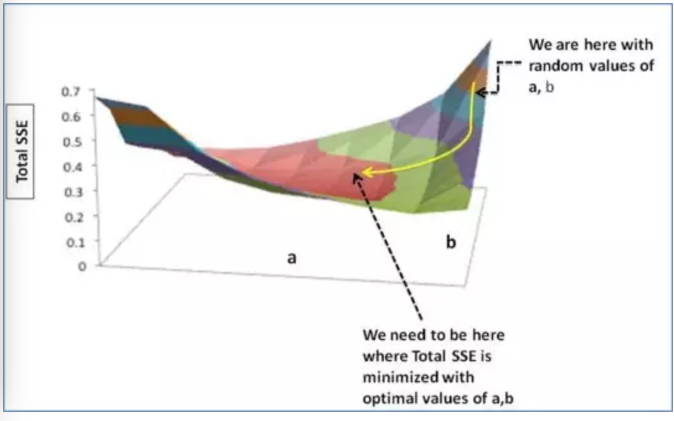
（右上角是我们随机的a,b所取得的SSE值，我们需要找到图中黑虚线所指的SSE最小值）

我们通过改变a,b来确保我们的SSE会向最小值方向移动，即沿黄线所指方向。至于改变a,b的规则：

a – ∂SSE/∂a
b – ∂SSE/∂b

所以，具体的公式就是：

New a = a – r * ∂SSE/∂a = 0.45 - 0.01 * 3.300 = 0.42
New b = b – r * ∂SSE/∂b = 0.75 - 0.01 * 1.545 = 0.73

在这里，r代表学习率 = 0.01，可以自设，是用来决定调整a,b快慢的。越大调整的越快，但越容易漏掉收敛的最佳点。

第四步：用新的a,b来求出新的SSE

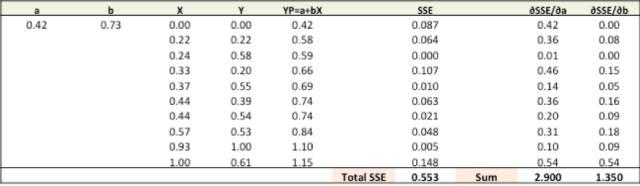
大家可以从图上看出，总的SSE值（Total SSE）从原来的0.677变为0.553。代表着我们的预测准度正在增加。

第五步：重复三四步直到调整a,b不会明显的影响SSE。到那时我们的预测准度就会达到最高

3、这就是梯度下降法，梯度更新公式不是推导而是创造然后定义出来的。

设想下有个函数，你的目标是：找到一个参数 $\theta$ 使得它的值 $Y$ 最小。但它很复杂，你无法找到这个参数的解析解，所以你希望通过梯度下降法去猜这个参数。问题是怎么猜？

对于多数有连续性的函数来说，显然不可能把每个 $\theta$ 都试一遍。所以只能先随机取一个 $\theta$ ，然后看看怎么调整它最有可能使得 $Y$ 变小。把这个过程重复n遍，自然最后得到的 $\theta$ 的估值会越来越小。

现在问题是怎么调整？既然要调整，肯定是基于当前我们拥有的那个参数 $\theta_t$ ，所以有了：

$\theta_{t+1}=\theta_t+\Delta$

那现在问题是每次更新的时候这个 $\Delta$ 应该取什么值？

我们知道关于某变量的（偏）导数的概念是指当（仅仅）该变量往正向的变化量趋向于0时的其函数值变化量的极限。 所以现在若求 $Y$ 关于 $\theta_t$ 的导数，得到一个值比如:5,那就说明若现在我们把 $\theta_t$ 往正向（即增大）一点点， $Y$ 的值会变大，但不一定是正好+5。同理若现在导数是-5，那么把 $\theta_t$ 增大一点点 $Y$ 值会变小。这里我们发现不管导数值 $\Delta$ 是正的还是负的（正负即导数的方向），对于 $\theta_t$ 来说， $-\Delta$ 的最终方向（即最终的正负号，决定是增（+）还是减（-））一定是能将Y值变小的方向（除非导数为0）。所以有了:

$\theta_{t+1}=\theta_t+(-\Delta)$

但是说到底， $\Delta$ 的绝对值只是个关于Y的变化率，本质上和 $\theta_t$ 没关系。所以为了抹去 $\Delta$ 在幅度上对 $\theta_t$ 的影响，需要一个学习率来控制： $\alpha \in (0,1]$ 。所以有了：

$\theta_{t+1}=\theta_t+(-\alpha\Delta)=\theta_t-\alpha\Delta$

而这里的 $\Delta$ 就是你1式中的那个偏导，而对于2式，就是有多少个参数，就有多少个不同的 $\Delta$ 。

现在分析在梯度下降法中最常听到的一句话：“梯度下降法就是朝着梯度的反方向迭代地调整参数直到收敛。” 这里的梯度就是 $\Delta$ ,而梯度的反方向就是 $-\Delta$ 的符号方向---梯度实际上是个向量。所以这个角度来说，即使我们只有一个参数需要调整，也可以认为它是个一维的向量。 整个过程你可以想象自己站在一个山坡上，准备走到山脚下（最小值的地方），于是很自然地你会考虑朝着哪个方向走，方向由 $-\Delta$ 的方向给出，而至于一次走多远，由 $|\alpha\Delta|$ 来控制。这种方式相信你应该能理解其只能找到局部最小值，而不是全局的。