操作系统——动态分配
写的时间早了,有些许漏洞和不足,请大家不要介意
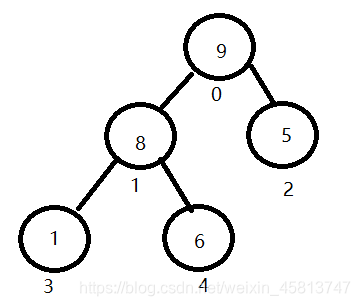
分配方式可分为四类:单一连续分配、固定分区分配、动态分区分配以及动态可重定位分区分配算法四种方式,其中动态分区分配算法就是此实验的实验对象。动态分区分配又称为可变分区分配,它是根据进程的实际需要,动态地为之分配内存空间。在实现动态分区分配时,将涉及到分区分配中所用的数据结构、分区分配算法和分区的分配与回收操作这样三方面的问题。动态分区分配又称为可变分区分配,它是根据进程的实际需要,动态地为之分配内存空间。在实现动态分区分配时,将涉及到分区分配中所用的数据结构、分区分配算法和分区的分配与回收操作这样三方面的问题。
大体流程图
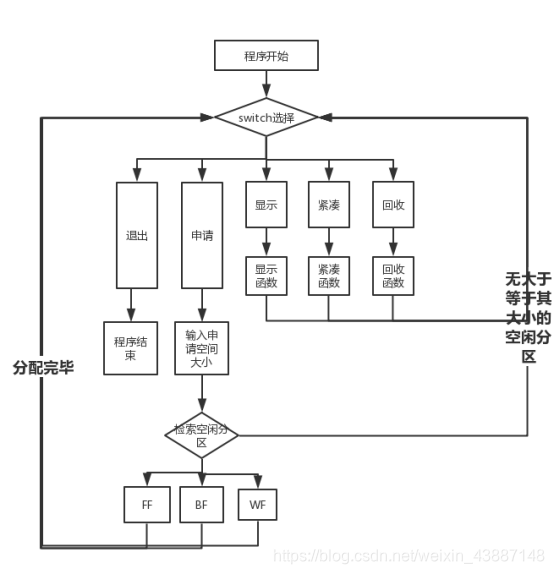
算法实现原理
定义的结构体:
struct Partition
{Partition* Back;//指向上一个分区 int Id;//分区号 int Size;//分区大小 int State;// 分区状态 0空闲 1占用 int Start_Address;//起始地址 int End_Address;//末尾地址 Partition* Next;//指向下一个分区
};首次适应算法:
空闲分区以地址递增的次序排列。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
void First_Fit(Partition* Partition_Table_Head, int Size) //首次适应算法
{int x = 1;Partition* p=NULL, * q=NULL;//定义两个指针p = Partition_Table_Head->Next;//将第一个数据节点赋给pwhile (p){if (p->Size >= Size && p->State == 0) break;p = p->Next;}//利用循环找到一个空闲的块,且其空间大小要大于等于要申请的空间if (p->Size == Size) p->State = 1;//若大小恰好合适,只需需改其状态即可else{q = (Partition*)malloc(sizeof(Partition));(p->Back)->Next = q;p->Size = p->Size - Size;q->Back = p->Back;q->Size = Size;q->Start_Address = p->Start_Address;q->End_Address = p->End_Address - p->Size;q->State = 1;q->Next = p;p->Back = q;p->Start_Address = q->End_Address + 1;}//若大于,则新建一个块,填写其数据,并修改当前块数据,加到其之前p = Partition_Table_Head->Next;while (p){p->Id = x;x++;p = p->Next;}//x重新给所有分区编号}最佳适应算法:
空闲分区按容量递增次序链接。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
void Best_Fit(Partition* Partition_Table_Head, int Size) //最佳适应算法
{int x = 1, count = 0, Remain_Size = 0;//conut用来保证第一个找到的分区可以直接用,Remain-size用来标识最好的大小Partition* p = nullptr;Partition* q = nullptr;//定义两个空指针p = Partition_Table_Head->Next;while (p){if (p->Size >= Size && p->State == 0)//找到一个空闲区,其大小大于等于要申请的大小{if (count == 0) //若是第一个找到的合适分区,则直接赋给q,并计算Remian_size{Remain_Size = p->Size - Size;q = p;count++;}else if (count != 0 && p->Size - Size < Remain_Size)若非第一个找到的合适分区,则比较Remain_size,选择小的重新赋给q{Remain_Size = p->Size - Size;q = p;}}p = p->Next;}
//同理,利用循环找到“最佳”的那个空闲区p = q;if (p->Size == Size) p->State = 1;else{q = (Partition*)malloc(sizeof(Partition));(p->Back)->Next = q;p->Size = p->Size - Size;q->Back = p->Back;q->Size = Size;q->Start_Address = p->Start_Address;q->End_Address = p->End_Address - p->Size;q->State = 1;q->Next = p;p->Back = q;p->Start_Address = q->End_Address + 1;}p = Partition_Table_Head->Next;while (p){p->Id = x;x++;p = p->Next;}
//同理,为新的分区前写信息
}最坏适应算法:
空闲分区按容量递减次序链接。每次分配内存时顺序查找空闲分区链(或空闲分区表),找到大小能满足要求的第一个空闲分区。
void Worst_Fit(Partition* Partition_Table_Head, int Size) //最坏适应算法
{int x = 1, count = 0, Remain_Size = 0;Partition* p = nullptr;Partition* q = nullptr;p = Partition_Table_Head->Next;while (p){if (p->Size >= Size && p->State == 0){if (count == 0){Remain_Size = p->Size - Size;q = p;count++;}else if (count != 0 && p->Size - Size > Remain_Size){Remain_Size = p->Size - Size; //道理同最佳适应算法,只是在这块选择Remain_size大的q = p;}}p = p->Next;}p = q;if (p->Size == Size) p->State = 1;else{q = (Partition*)malloc(sizeof(Partition));(p->Back)->Next = q;p->Size = p->Size - Size;q->Back = p->Back;q->Size = Size;q->Start_Address = p->Start_Address;q->End_Address = p->End_Address - p->Size;q->State = 1;q->Next = p;p->Back = q;p->Start_Address = q->End_Address + 1;}p = Partition_Table_Head->Next;while (p){p->Id = x;x++;p = p->Next;}}
回收:
对回收一个分区的四种情况,进行处理
void Recycle(Partition* Partition_Table_Head) //回收
{int x = 1, id;Partition* p=NULL, * q=NULL;//定义两个空指针p = Partition_Table_Head->Next;cout << "请输入要回收分区的分区号 :" << endl;cin >> id;while (p){if (p->Id >= id) break;p = p->Next;} p->State = 0; //根据输入要回收的分区号,使p指向它,并修改其状态为空闲check_again: if (p->Back != NULL && (p->Back)->State == 0) //检查上一个分区是否为空,若为空,则合并
{p->Size = p->Size + (p->Back)->Size;p->Start_Address = (p->Back)->Start_Address;if ((p->Back)->Back != NULL) ((p->Back)->Back)->Next = p;else p->Back = NULL;q = p->Back;p->Back = (p->Back)->Back;free(q);goto check_again; //再次检查,避免连续的空闲(虽然没可能)
}if (p->Next != NULL && (p->Next)->State == 0) //检查下一个分区是否为空i,若为空,则合并
{p->Size = p->Size + (p->Next)->Size;p->End_Address = (p->Next)->End_Address;q = p->Next;if ((p->Next)->Next != NULL) p->Next = (p->Next)->Next;else p->Next = NULL;free(q);goto check_again; //再次检查,避免连续的空闲(虽然没可能)
}p = Partition_Table_Head->Next;
while (p)
{p->Id = x;x++;p = p->Next;
} //重新编号}算法效果
初始化空白分区并显示进程目录
跳过
首次适应算法、
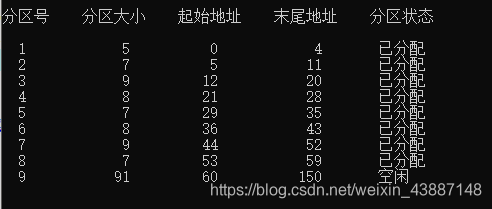
回收
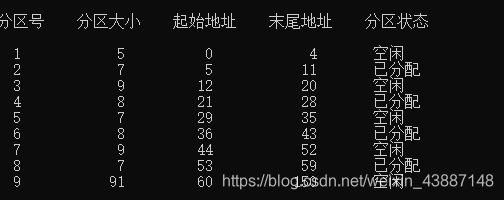
回收8
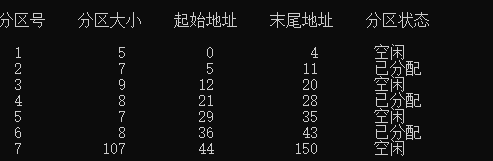
最佳适应算法
申请大小为7的分区
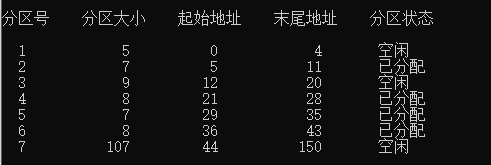
最坏适应算法
申请大小为5的分区
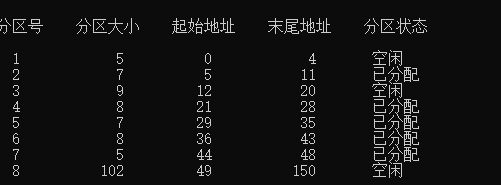
每种算法的优劣
4.1首次适应算法:
优点:高址部分的大的空闲分区得到保留,为大作业的内存分配创造了条件;
缺点:(1)每次都是优先利用低址部分的空闲分区,造成低址部分产生大量的外 部碎片
(2)每次都是从低址部分查找,使得查找空闲分区的开销增大;
4.2最佳适应算法:
优点:第一次找到的空闲分区是大小最接近待分配内存作业大小的;
缺点:产生大量难以利用的外部碎片
4.3最坏适应算法:
优点:效率高,分区查找方便;
缺点:当小作业把大空闲分区分小了,那么,大作业就找不到合适的空闲分区。