0、其他补充

均匀线阵波束形成器的信噪比增益上确界可由下式表示：

$SINR_{OPT,OUT} = SINR_{IN}+10\lg M$

其中 $M$ 为阵元数，所以为了方便起见，一般的稳健自适应波束形成算法在仿真过程中的阵元数量均设置为10。

阵列的导向矢量可由下式表示：

$\pmb a(\theta_k)=\left[1\quad\exp(-\mathrm j2\pi\frac d\lambda\sin\theta_k)\quad\cdots\quad\exp(-\mathrm j2\pi(M-1)\frac d\lambda\sin\theta_k)\right]^\top$

以首个阵元为参考阵元，其中 $d$ 为阵元间距，一般情况下为半波长， $\lambda$ 为波长，当然，一些文献中的导向矢量也有以余弦函数代替上式中的正弦函数的，这只是入射角的定义不同。

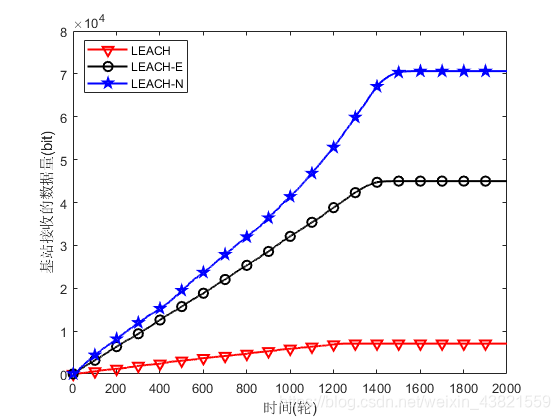
1、有限快拍数问题

事实上限制于设备采样率等诸多原因，实际环境中提供的数据往往是小样本条件下的，因此对于一些基于协方差矩阵的自适应波束形成算法，有限采样快拍数的影响主要表现在协方差矩阵失真问题上，因而进一步影响矩阵在特征分解过程中的特征值紧致性(主要为小快拍数下大特征值过大，小特征值过小的问题)，以及特征向量的偏移。

2、输入信号信噪比问题

对于一些早期的基于MVDR的波束形成器，在高输入信噪比下输出信噪比下降的问题是影响其性能的一个问题，其原因主要在于早期波束形成器通常将接收信号的协方差阵视为干扰加噪声协方差阵的近似，因此在高信噪比下，求解权向量的过程中，协方差矩阵中的信号分量会与期望信号的导向矢量产生自消的现象，即期望信号误被当作干扰信号以构造零陷进行抑制。

3、先验信号方向误差问题

一般的波束形成器需要至少提供期望信号方向等一系列先验信息以求解权向量，这一系列以方向为主的先验信息一般由DOA算法提供。因此，非精准的先验信号方向误差会使得信号来波方向不在实际增益最大处。以传统的均匀线性全向增益接收阵列为例，空间平面波到达时间与相位差使之成为一空域FIR滤波器(或MA过程)，这也是其波束图尖锐零陷与平稳谱峰的体现，从而在不考虑波束形成器增益上限的情况下，使得期望信号方向误差对波束形成器的性能相比于干扰信号方向误差对波束形成器的性能影响小。

4、阵元的幅度与相位扰动误差问题

理想阵元应是全向同性增益的，然而在实际情况中，即使是在校准过后阵元也会存在轻微扰动。该问题通常在仿真过程中以加权系数的形式在导向矢量的各个分量中体现，且一般服从正态分布。例如：幅度误差服从 $\mathcal{N}\left(1,0.1^2\right)$ 的正态分布，而相位误差服从 $\mathcal{N}(0,(0.01\pi)^2)$ 的正态分布。

5、阵列分布误差问题

实际阵列排布过程中会产生阵列分布误差，使得其不会严格地各阵元等间距，这一问题在以水下拖曳阵/垂直阵的应用场景中尤为明显，对阵列导向矢量的影响。以第 $m$ 个阵元为例，该阵元的参考距离由 $(m-1)d$ 变为 $d_m$ ，对导向矢量的影响主要在其分量的相位上。

6、互耦效应问题

互耦效应通常为天线处于工作状态时天线阵元之间存在的电磁能量耦合现象，互耦效应引起天线阵元失配使接收信号畸变，进一步影响接收信号及阵列的协方差矩阵，从而影响阵列的波束图形状及增益。一般情况下，阵列中的第 $i$ 个阵元与第 $j$ 个阵元之间的互耦系数 $[C]__{i,j}$ 可表示为：

$[C]_{i,j}=\begin{cases}1,i=j\\ c_k,k=\big|i-j\big|\leqslant\bar{P}-1,i\neq j\\ 0,\text{otherwise}\end{cases}$

理想情况下，互耦系数与阵元间距成反比，且当阵元间距超出一定距离时，该两个阵元之间的互耦效应可视为0。又因为互耦效应的作用是相互的，因此阵列互耦系数矩阵 $C$ 呈现出对称托普利茨特征。则阵列的接收信号可改写为：

$x\big(t\big)=CAs\big(t\big)+n\big(t\big)$

可以看作是对阵列导向矢量产生的直接影响。

7、信号由于多径效应产生的局部散射问题

在一些强多径环境中阵列接收的信号是存在空域弥散现象的，即在一个小角度范围内信号分别从视距路径与非视距路径先后到达接收阵列。以期望信号为例，该问题可表示为：

$\tilde{\textbf{x}}_s(k)=\textbf{a}(\theta_0)s_0(k)+\sum\limits_{p=1}^{P_{NLOS}}\textbf{a}\left(\theta_{0p}\right)s_{0p}(k)$

其中 $\tilde{\textbf{x}}_s(k)$ 为阵列接收的含多径的信号，等号右边前半部分为视距路径，后半部分为非视距路径， $\theta_{0p}$ 一般被视为服从均值为 $\theta_0$ 的高斯独立同分布的角度分布， $P_{NLOS}$ 为非视距路径数。又因为一般仿真过程中接收的信号为了不相关起见均设置为了正态序列，因此实际上带有不同延迟的非视距路径与视距路径信号之间是非相关的。