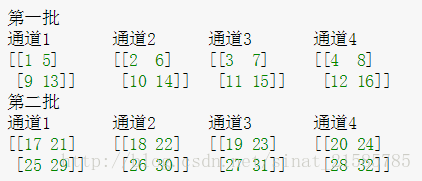
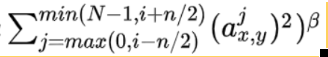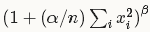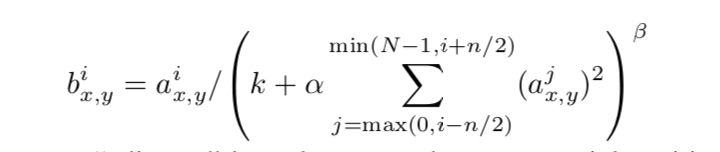最大公约数：

 

“最大公因数，也称最大公约数、最大公因子，指两个或多个整数共有约数中最大的一个。a，b的最大公约数记为（a，b），同样的，a，b，c的最大公约数记为（a，b，c），多个整数的最大公约数也有同样的记号。”

采用欧几里得算法：

所以我们设计欧几里得算法的C语言程序：

#include<stdio.h>
int Eucl(int x, int y)
{int z = 0;while (y != 0){z = y;y = x % y;x = z;}return x;
}
int main()
{int A = 0;int B = 0;while (scanf("%d %d", &A, &B) != EOF){printf("%d\n",Eucl(A, B));}return 0;
}

最小公倍数：

“两个或多个整数公有的倍数叫做它们的公倍数,其中除0以外最小的一个公倍数就叫做这几个整数的最小公倍数。整数a,b的最小公倍数记为[a,b],同样的,a,b,c的最小公倍数记为[a,b,c],多个整数的最小公倍数也有同样的记号。”

最小公倍数的计算方法是：

num1与num2的乘积除以其最大公约数即可。

#include<stdio.h>
int Eucl(int x, int y)
{int z = 0;while (y != 0){z = y;y = x % y;x = z;}return x;
}
int main()
{int A = 0;int B = 0;while (scanf("%d %d", &A, &B) != EOF){if (Eucl(A, B) != 1){printf("%d\n", A * B / Eucl(A, B));}elseprintf("%d\n", A * B);}return 0;
}