文章目录
- 前言
- 一、题目
- 二、使用步骤
- 1.递归构建博弈树
- 2.α-β剪枝算法
- 3.博弈树可视化
- 4.测试实例
- 5.结果展示
- 6.全部代码
- 总结
前言
使用Python编程实现博弈树的构建,实现利用MinMax方法补全博弈树缺失值,并结合α-β剪枝算法,实现博弈树的剪枝。实现了整体算法与博弈树的可视化。
一、题目
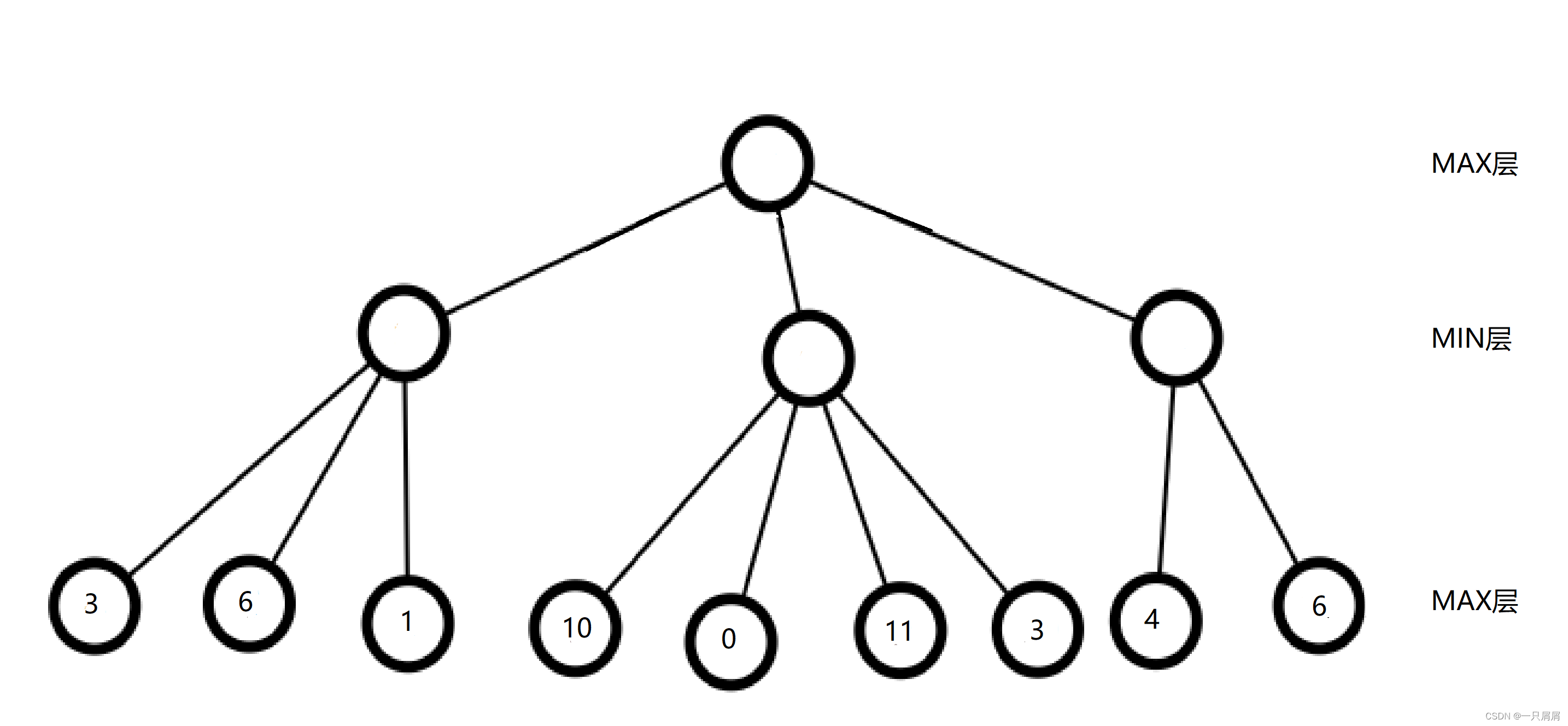
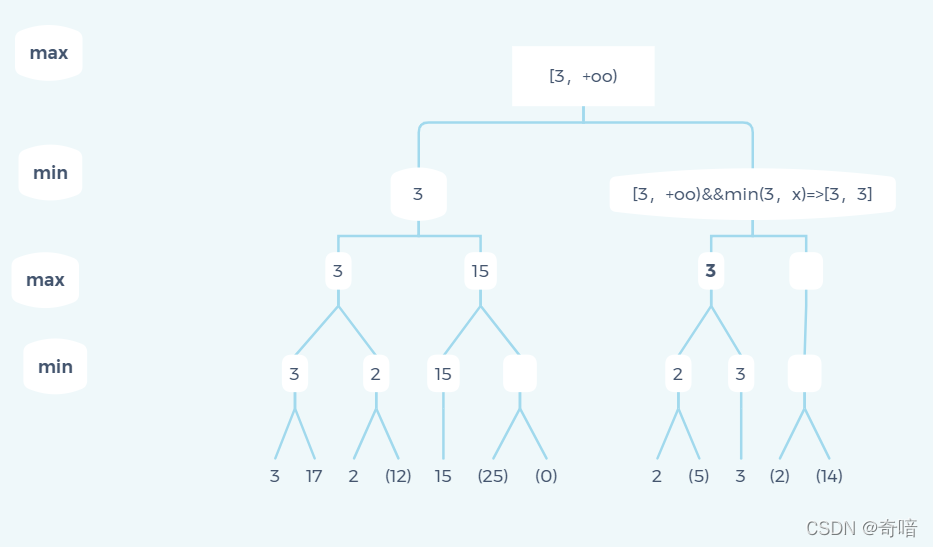
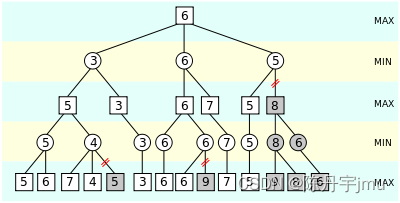
博弈树初始结构如下
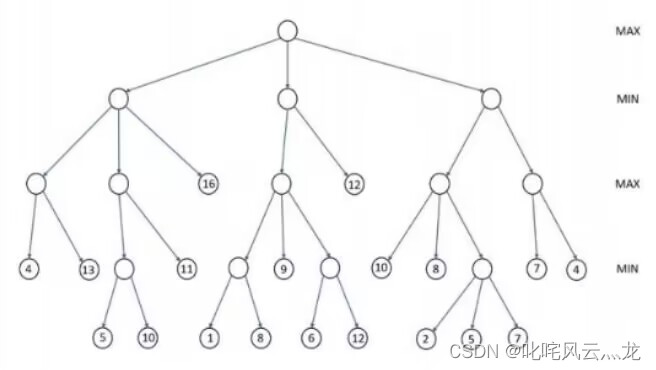
二、使用步骤
1.递归构建博弈树
代码如下:
class Node(object):def __init__(self, val: int=0, max: bool=True) -> None:'''val: 节点值max: 是否为max层childern: 子节点列表'''self.val = val # 该节点的值self.max = max # 该层是否为max层,默认顶层节点为max层self.children : list = [] # 该节点的子节点class Tree(object):def __init__(self) -> None:'''data_list: 数据列表上图所示列表示例:[[[4,13],[[5,10],11],16],[[[1,8],9,[6,12]],12],[[10,8,[2,5,7]],[7,4]]]其中节点值为一个int型数值,含有其他子节点的构建为列表'''self.root = Node() # Node(),根节点def build_tree(self, data_list, root) -> None:# 递归构建博弈树for i in range(len(data_list)):is_max = root.maxif is_max == True:is_max = False # min层else: is_max = True # max层if type(data_list[i]) is tuple:# 该节点为叶节点,直接添加节点值for val in data_list[i]:root.children.append(Node(val, is_max))elif type(data_list[i]) is int:# 该节点为叶节点,直接添加节点值root.children.append(Node(data_list[i], is_max))elif type(data_list[i]) is list:# 该节点含有子节点,递归创建if type(data_list[i]) is int:# 该节点为叶节点,直接添加节点值root.children.append(Node(data, is_max))elif type(data_list[i]) is list:# 该节点含有子节点,递归创建root.children.append(Node(max=is_max)) # 添加子节点self.build_tree(data_list[i], root.children[i])
2.α-β剪枝算法
代码如下:
class AlphaBeta(object):def __init__(self, tree, auto=False) -> None:'''tree: 博弈树auto: 补全全部节点值,默认不补全选择不补全时,可视化过程为剪枝过程,节点为0的子节点为剪掉的节点'''self.tree = tree # 博弈树self.auto = auto # 补全全部节点值,可选参数,默认不补全self.deep = 0 # 节点深度self.alpha = -float('inf')self.beta = float('inf')if self.auto:# 补全博弈树self.complement_value(self.tree.root)def get_value(self, node) -> int:# 获取节点值return node.valdef is_leaf(self, node) -> bool:# 判断是否为叶节点if len(node.children) == 0:return Trueelse:return Falsedef complement_value(self, node): # 补全博弈树,可选# 根据MinMax规则补全博弈树if self.is_leaf(node):return self.get_value(node)if self.get_value(node) != 0:return self.get_value(node)val_list = []for child in node.children:temp = self.complement_value(child)val_list.append(temp if temp is not None else child.val)if node.max:node.val = max(val_list)else:node.val = min(val_list)def max_value(self, node, alpha, beta):if self.is_leaf(node):# 当前节点为叶节点return self.get_value(node)best = -float('inf') # 初始化无穷小for child in node.children:best = max(best, self.min_value(child, alpha, beta))if best >= beta:return bestalpha = max(alpha, best)node.val = bestreturn bestdef min_value(self, node, alpha, beta):if self.is_leaf(node):# 当前节点为叶节点return self.get_value(node)best = float('inf') # 初始化无穷大for child in node.children:best = min(best, self.max_value(child, alpha, beta))if best <= alpha:return bestbeta = min(beta, best)node.val = bestreturn bestdef alpha_beta(self): best = self.max_value(self.tree.root, self.alpha, self.beta)# return bestfor child in self.tree.root.children:if best == child.val:return child
3.博弈树可视化
代码如下:
import matplotlib.pyplot as pltclass ShowTree(object):def __init__(self, tree) -> None:'''tree: 博弈树'''self.tree = tree # 博弈树self.__num_of_leafs = self.get_num_of_leaf(self.tree.root) # 叶节点数量self.__tree_depth = self.get_tree_depth(self.tree.root) # 树深度# 初始化箭头格式self.arrow_args = dict(arrowstyle="<-")@propertydef num_of_leafs(self):return self.__num_of_leafs@propertydef tree_depth(self):return self.__tree_depthdef get_num_of_leaf(self, node):# 获取叶节点数量num_of_leafs = 0if len(node.children) == 0:# 该节点为叶节点,叶节点数量+1num_of_leafs += 1else:for child in node.children:num_of_leafs += self.get_num_of_leaf(child)return num_of_leafsdef get_tree_depth(self, node):# 获取树的最大深度max_tree_depth = 0if len(node.children) == 0:# 该节点为叶节点,深度为1max_tree_depth += 1else:for child in node.children:this_depth = 1 + self.get_tree_depth(child)if this_depth > max_tree_depth:max_tree_depth = this_depthreturn max_tree_depthdef box(self, node):# 设置文本框样式if node.max:boxstyle = "square"else:boxstyle = "circle"return dict(boxstyle=boxstyle,fc="0.8")def plot_node(self, node, centerPt, parentPt):node_type = self.box(node)# node_type = dict(boxstyle="round4",fc="0.8")ShowTree.plot.ax1.annotate(node.val, xy=parentPt, \xycoords='axes fraction',xytext=centerPt, textcoords='axes fraction',\va="center",ha="center", bbox=node_type, arrowprops=self.arrow_args)@staticmethoddef plot_tree(tree, node, parentPt):numLeafs = ShowTree.get_num_of_leaf(tree, node) # 计算树的宽度depth = ShowTree.get_tree_depth(tree, node) # 计算树的高度# 输入的第一个节点first_node = nodecntrPt = (ShowTree.plot_tree.xOff + (1.0 + float(numLeafs)) / 2.0 / ShowTree.plot_tree.totalW, ShowTree.plot_tree.yOff)# 叶子节点ShowTree.plot_node(tree, first_node, cntrPt, parentPt)# 减少y的便偏移ShowTree.plot_tree.yOff = ShowTree.plot_tree.yOff - 1.0 / ShowTree.plot_tree.totalD for child in node.children:if len(child.children) == 0:ShowTree.plot_tree.xOff = ShowTree.plot_tree.xOff + 1.0 / ShowTree.plot_tree.totalWShowTree.plot_node(tree, child, (ShowTree.plot_tree.xOff, ShowTree.plot_tree.yOff), cntrPt)else:ShowTree.plot_tree(tree, child, cntrPt)ShowTree.plot_tree.yOff = ShowTree.plot_tree.yOff + 1.0 / ShowTree.plot_tree.totalD@staticmethoddef plot(tree):'''tree: 需要绘制的树,类型为ShowTree()'''fig = plt.figure(1, facecolor='white')# Clear figure清除所有轴,但是窗口打开,这样它可以被重复使用fig.clf()axprops = dict(xticks=[], yticks=[])ShowTree.plot.ax1 = plt.subplot(111, frameon=False, **axprops)# ShowTree.plot_node(show_tree, show_tree.tree.root, (0.5,0.1),(0.1,0.5))ShowTree.plot_tree.totalW = float(ShowTree.get_num_of_leaf(tree, tree.tree.root))ShowTree.plot_tree.totalD = float(ShowTree.get_tree_depth(tree, tree.tree.root))ShowTree.plot_tree.xOff = -0.5 / ShowTree.plot_tree.totalWShowTree.plot_tree.yOff = 1.0ShowTree.plot_tree(tree, tree.tree.root,(0.5, 1.0))plt.show()
4.测试实例
代码如下:
if __name__ == '__main__':data = [[[4,13],[[5,10],11],16],[[[1,8],9,[6,12]],12],[[10,8,[2,5,7]],[7,4]]] # 初始博弈树值列表tree = Tree() # 实例化空树tree.build_tree(data, tree.root) # 递归构建博弈树alpha_beta = AlphaBeta(tree, auto=True) # α-β剪枝best = alpha_beta.alpha_beta() # 获取结果print(best.val)from plot_tree import ShowTreeshow_tree = ShowTree(tree) # 实例化博弈树可视化算法show_tree.plot(show_tree) # 可视化博弈树
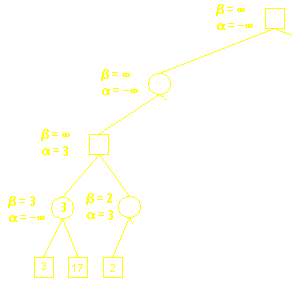
5.结果展示
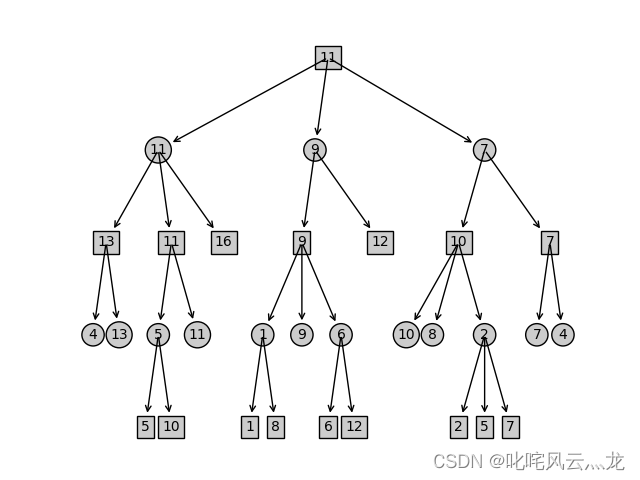
6.全部代码
全部代码如下alpha_beta.zip
总结
利用Python编程实现了α-β剪枝算法,并利用matplotlib实现了博弈树的可视化。