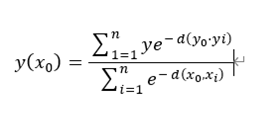​
 ​​ ​决策树后剪枝算法（一）代价复杂度剪枝CPP
 ​​ ​决策树后剪枝算法（二）错误率降低剪枝REP
 ​​ ​决策树后剪枝算法（三）悲观错误剪枝PEP
 ​​ ​决策树后剪枝算法（四）最小错误剪枝MEP
 ​​ ​
​ ​ 剪枝，是一个“用准确性换取简单性”的思想。它允许决策树对训练集过拟合，再通过删除对泛化精度无贡献的子分支，从而修剪出一颗较小的树。以下列出几种较常见的后剪枝算法，及其机制对比：

	CCP	REP	PEP	MEP
剪枝方式	自底向上	自底向上	自顶向下	自底向上
计算复杂度	$O(n^2)$	$O(n)$	$O(n)$	$O(n)$
误差估计	标准误差	剪枝集上误差	连续性矫正	概率估计
是否需要额外剪枝集	否	是	否	否

​ ​

（4）最小错误剪枝（MEP）

​ ​ 1986年Niblett和Bratko提出了最小错误剪枝。最小错误剪枝采用自底向上的方式对决策树进行剪枝，也是后剪枝的一种。最小错误剪枝的主要思想是通过分别计算剪枝前与后的期望错误率$E_k$，进行判断。

​ 

（4.1）数学推导

​ 评价标准:
$$E_k=\frac{n-n_c+k-1}{n+k}$$
​ 解读:

• $E_k$为期望错误率，为评价是否剪枝标准。

• $n$为样本数，$n_c$为结点最多类别$c$的样本数, $k$为决策树分类类别总数。

• 该公式需假设每个类别概率相等。

​ ​ 要计算期望错误率，首先需引入错误率计算，反向思考则为计算$P_c(T)$（1 - 节点$T$分类为某类别$c$的概率），直观思考可得：
$$P_r(T)=\frac{n_c}{n}$$
​ ​ 但这样做是有问题的，因为我们仍未知各个样本属于类别$c$的概率，即贝叶斯思维中的先验概率。这便是我们的假设前提“每个类别概率相等”的作用，故有关于节点$T$各样本是属于类别$c$的先验概率为:
$$P{r}_c(T)=\frac{1}{k}$$
​ ​ 故引出最终的后验概率，节点$T$分类为某类别$c$的概率：
$$P_c(T)=\frac{n_c+P{r}_c(T)\times m}{n+m}(其中m为先验概率影响因子)$$
​ ​ 因而求得节点$T$分类为某类别$c$的错误率：
$$\begin{gathered} Erro{r}_c(T)=1-P_c(T) \\ =\frac{n-n_c+m(1-P{r}_c(T))}{n+m} \end{gathered}$$
​ ​ 因一个节点只能有一个类别，且判断方式常为多数表决，则节点$T$的错误率和最大类别$c$直接挂钩，可表示为:
$$Error(T)=Erro{r}_c(T)$$
​ ​ 故期望错误率$E_k$则转换为，求一个恰当的影响因子$m$的函数，其中一种思路为，求：
E k = min ⁡ { 1 − P c ( T ) } = = min ⁡ { n − n c + m ( 1 − P r c ( T ) ) n + m } E_k=\min\{1-P_c(T)\}==\min\{\frac{n-n_c+m(1-Pr_c(T))}{n+m}\} Ek​=min{1−Pc​(T)}==min{n+mn−nc​+m(1−Prc​(T))​}
​ ​ 即求解$m$函数的最小值。

​ ​ 为简便计算，从规律进行总结，当$m=0$时，可考虑先验概率影响为0；而$m\to \infty$时，先验概率影响程度无穷大。则可近似将$m$等价于类别总数$k$，即类别总数为0，先验概率不予考虑；类别总数较大，先验概率至关重要。

​ ​ 故得到简化公式：
$$E_k=\frac{n-n_c+k-1}{n+k}$$

​ 

（4.2）算法流程

​ ​ 考虑决策树上每个中间节点作为剪枝候选对象，自底向上遍历，判断是否剪枝步骤如下：

• （1）删除以此节点为根的子树，使其成为叶子结点。
• （2）根据多数表决法，赋予该节点关联的训练数据类别。
• （3）比较删除前后错误样本数，判断是否剪枝该节点。

​ 

（4.3）例题计算

​ ​ 下面举一个例子进行说明，下图待剪枝决策树有三个类别，每个节点类别及各分类样本数均如图矩形框中列出。

​ 
​ ​ 节点"node 27"
$$\begin{gathered} 剪枝后：E_k(t)=\frac{20-15+3-1}{20+3}=0.304 \\ 剪枝前：E_k(T_t)=\frac{17}{20}\times (\frac{17-15+3-1}{17+3})+\frac{3}{20}\times (\frac{3-3+3-1}{3+3})=0.220 \\ 注：剪枝前的计算过程为T_t下叶子节点计算结果加权求和 \end{gathered}$$
​ ​ 可得剪枝后期望错误率增加，故不可剪枝。

​ 

​ ​ 节点"node 26"

​ ​ 节点"node 26"的计算结果也是不可剪枝，请自行验证。(0.447 / 0.370)

​ 

（4.4）代码实现

​ C4.5算法及MEP剪枝手写实现

链接：https://pan.baidu.com/s/1JcwHWn7uAzYdahAV6e2GJw?pwd=94bm 
提取码：94bm

​ 代码参考：http://www.hzcourse.com/web/refbook/detail/9970/226

————————————————————————————————————————————————————————————

​ 参考资料：

​ [1] 现代决策树模型及其编程实践 黄智濒 编著

​ [2] https://www.bilibili.com/video/BV1No4y1o7ac?p=48