背景

  由于笔者最近要写人工智能课的大作业，所以这两天在学习博弈论相关的知识，但网上对alpha-beta剪枝的原理讲的都不是很清晰，很多细节都忽略了，让初学者会有一种脑子说会了，但手并不会的感觉，导致一写起代码就懵，所以笔者决定整理一下知识点，让初学者更容易接受。本文适合想深入理解算法原理的读者，如果您只是需要在工程中使用，请直接到文章最后ctrl cv代码即可。

  不管是alpha-beta剪枝算法还是它的前身Max-Min算法，都是用于在不同阵营进行博弈的问题中计算理论最优解。注意这里的两个关键词：不同阵营、理论最优解。

  我们平时玩的五子棋、象棋等游戏中，玩家被分为两个阵营，且在棋盘上所有棋子位置一定时，两方进行的操作不同，因为双方需要考虑己方棋子移动的最优解并且只能移动己方棋子，这种游戏可以使用上述两种算法。但还有一种游戏，它是没有严格划分阵营的，也就是说如果当前游戏的局面一定，对于两个玩家来说，他们选择的理论最优解应该是相同的，比如两个人从n个石子中取走石子，每次至多可以取m(0 < m < n)个石子，取完石子的人胜利，这类游戏我们乘为Nim游戏，本文中不过多介绍，有兴趣了解的请查找Nim游戏和SG函数相关资料。

  我们再来看第二个关键词：理论最优解，我们在算法中所做的所有推演，都是基于对手也会选择对它理论上的最优解，但在实际的人机对战中，人类很难做到这一点，况且在机机对战中，如果各自的评价函数（即量化当前操作的优劣）不同，各自的理论最优解也不同。

Max-Min算法

  在讲alpha-beta剪枝之前，不得不提的就是它的前身Max-Min算法，可以说Max-Min算法是灵魂，alpha-beta剪枝不过是加了一点trick节约搜索资源。

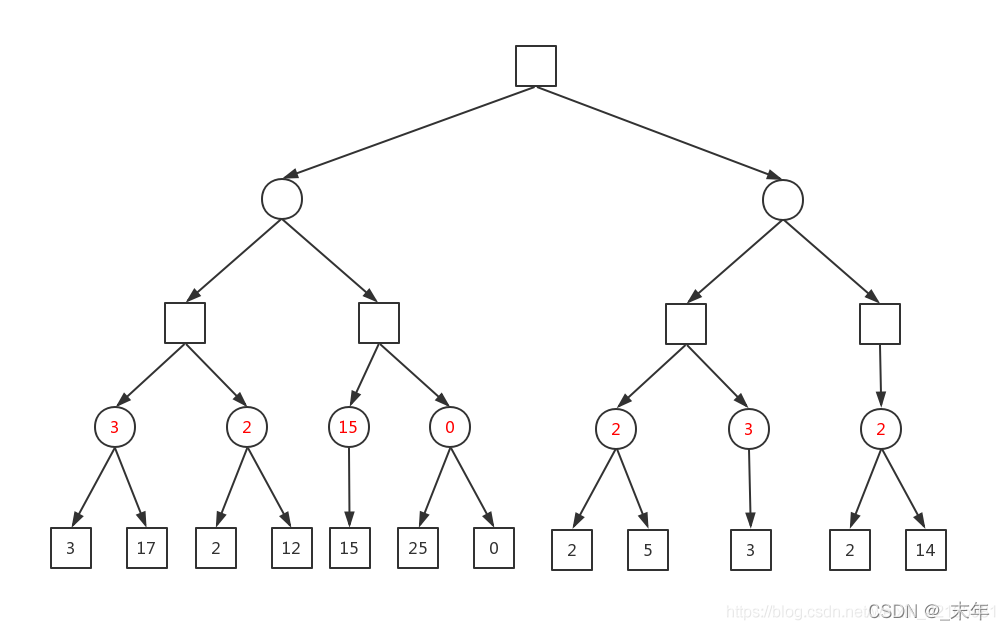图源：Bug_Programmer

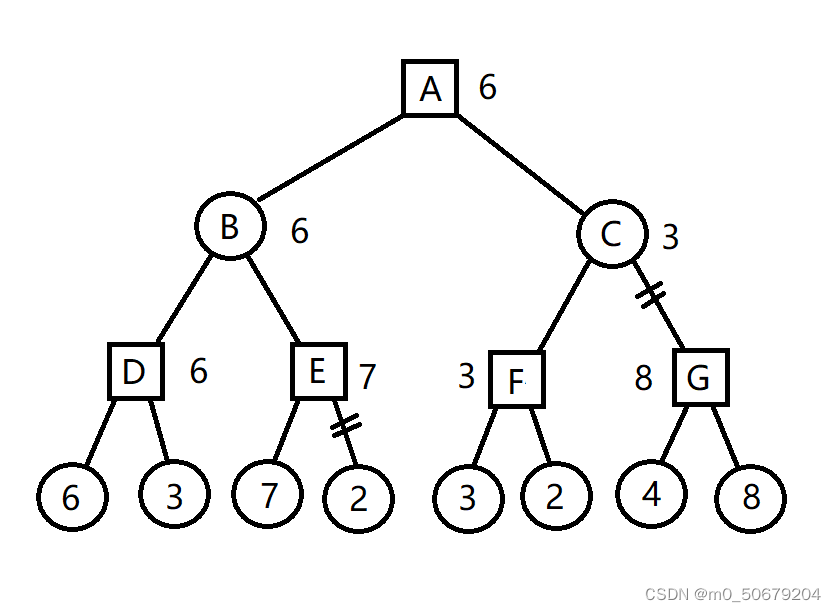
  这是一个经典的博弈树，它记录了博弈中所有可能的情况。注意到，博弈进行到叶结点即结束，这里需要说明，搜索结束不代表游戏结束。比如在五子棋中，如果我们想一直搜索直到游戏结束，复杂度是指数级增长的，计算机没有那么多计算资源也没必要使用那么多计算资源，我们可以设置一个最大搜索深度，当博弈树搜索到最大深度时开始计算当前最优解，换句话来说，我们在搜索范围过大时，只考虑局部最优解而不去考虑全局最优解。

  Max-MIn算法将决策树中不同深度的层分为Max层和Min层，Max层选择自己的最优解，Min层选择对方的最优解。决策树的根结点是自己当前所选择的操作，显然它是一个Max层，往后以此类推，方形代表Max层，圆形代表Min层。

  在确定完Max和Min层后，我们就要开始计算每个结点能取到的最优解了。这个最优解是经过评价函数量化的，不同游戏的评价函数定义不同，你可以根据自己的需求个性化选择评价函数，但不管是什么定义方式，它本质上就是一个量化当前局面对自己来说优劣的函数。

  该算法的核心在于逆推，即从当前操作所导致的结果推出当前操作的最优解。 当搜索到叶结点时，我们计算所有叶节点的评价值，然后计算父结点的评价值，计算方式为：Max层的结点取它的子结点中的最大值，Min层的结点取它的子结点中的最小值。 用图中最左面的分支来举例，当进行到Min层时，此时他有两个选择，评价值分别为3和17，那么作为你的对手，他一定会让你的评价值最小，因此他会选择评价值为3的操作，同理可知Max层选择评价值最大的操作。

  由此我们就可以计算根结点的操作，即选择当前能达到的最大评价值所对应的操作。

alpha-beta剪枝

  我们终于开始讲这个神秘的alpha-beta剪枝算法了，如果你理解了Max-Min算法，那么理解这个应该也很轻松。

  我们很容易发现，Max-Min算法有它明显的缺陷——计算量大，即使我们做了搜索深度限制，计算量仍十分庞大，算法工程师们总是不满足暴力搜索的，因此就有了alpha-beta剪枝算法。

  现在请思考一个问题，如果你已经有了一个评价值为10的操作，那么再遍历其他结点时，你发现它最大能达到的评价值是5，那么你还会继续遍历这个结点的其他子结点吗？显然不会，因为你已经有了一个更优的选择了，除非有一个比10更大的评价值，否则你不会再搜索下去。同理，如果你的对手已经有了一个评价值为5的操作，那么它还会让你选择评价值更大的操作吗？也不会，因为它是你的对手，理论上它总想让你玩的最不舒服。

  理解了这个，你就理解了alpha-beta剪枝的精髓——剪掉那些一定不会选择的分支。

  下面我们来详细介绍一下这个“聪明”的算法。

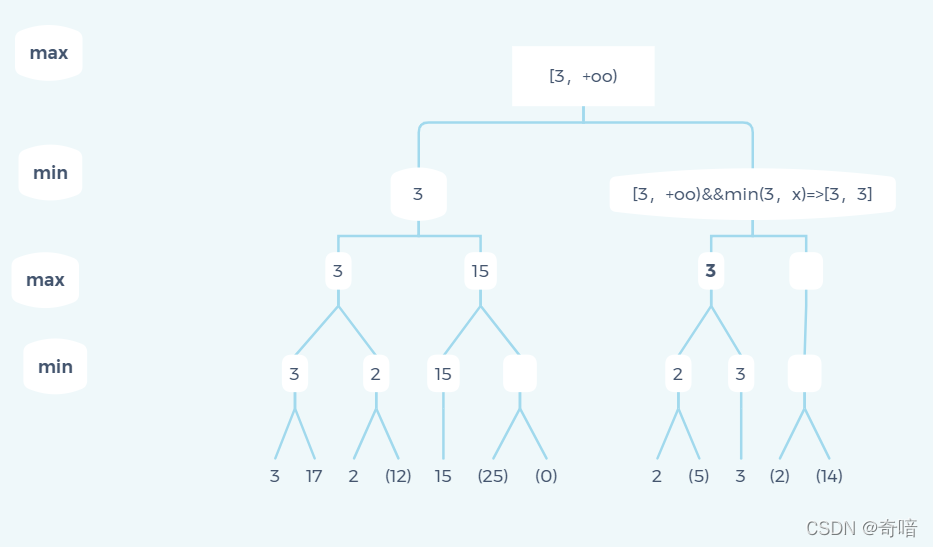
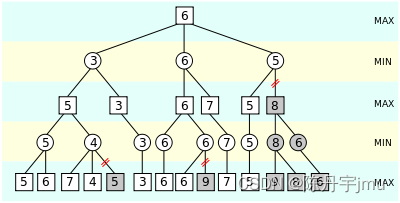
图源：急流

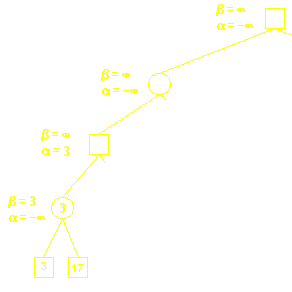
  上图是我们用DFS搜索第一条路径的结果，两个叶结点分别是3和17，当我们搜索到第一个叶结点3时，此时17的结点还未被搜索到，那么由于它的父结点在Min层，所以它的父结点一定会选择一个评价值小于等于3的值， 请仔细思考这句话，很重要！换句话说，目前来看，父结点的上界是3，由此引出该算法的第一个参数——β，它是一个结点所能选取的评价值的上界。现在我们假设两个叶结点在Min层，它们的父结点在Max层，此时由于我们搜索的顺序仍是从左向右，父结点一定会选择一个评价值大于等于3的值， 也就是说父结点评价值的下界是3，由此引出该算法的第二个参数——α，它是一个结点所能选取的评价值的下界。

        
知道了α和β的定义，我们来介绍一下alpha-beta剪枝中最重要的性质：
1. Max层的α = max(α， 它的所有子结点的评价值)，Max层的β = 它的父结点的β
2. Min层的β = min(β， 它的所有子结点的评价值)，Min层的 α = 它的父结点的α
3. 当某个结点的 α >= β，停止搜索该节点的其他子结点
4. 叶结点没有 α 和 β

    
我们一一说明这四条性质：
首先我们假设所有非叶结点的α初始化为负无穷，β初始化为正无穷。

1. 若Max层中发现有一个子结点的评价值比当前所能达到的评价值更大，换句话说就是子结点的操作更优，那么将当前所能达到的评价值换成该子节点的评价值。并且由于它的父结点是从该Max层中选择最小的评价值，那么他就要判断一下当前的α是否大于它父结点的β。为了方便起见，我们将父结点的β赋给它自己的β，这样我们只需要比较它自己的α和β就可以了。
2. 跟第一条类似，如果发现子结点中有比当前更优的操作（对对手更优，即对自己更差），那么就替换β，同时比较父结点最优解与当前解的大小，如果父结点已经有一个更优解，则不必继续搜索了。
3. Max层中，若某个结点的最优解已经大于它的父结点的最差解，则不必继续搜索，剪枝；Min层中，若某个结点的最差解已经小于它的父结点的最优解，则不必继续搜索，剪枝。
4. 由于叶结点没有子结点，自然不需要计算 α 和 β。

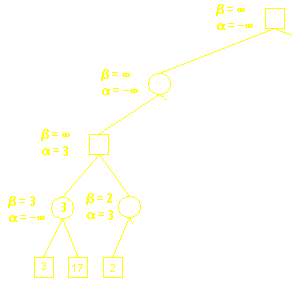图源：急流
（原谅我懒得画图）

代码

棋类游戏博弈

        import numpy as npMAXINF = 9999999999
MININF = -MAXINFclass Chess(object):def __init__(self, prior="man"):self.player = prior # 默认玩家先手self.man_steps = 0self.machine_steps = 0self.cols  = 3 # 棋盘的列数self.rows  = 3 # 棋盘的行数self.tree_depth = self.rows * self.cols # 博弈树的最大深度self.chessboard = np.zeros((self.rows, self.cols)) # 初始化棋盘，玩家下棋记为1，电脑下棋记为-1self.best_status = () # 当前最优操作# 评价函数def Evaluate(self):if self.Winner() == "machine":return 100 - self.machine_stepselif self.Winner() == "man":return -100 + self.man_stepselif self.Winner() == "tie":return 0def DetermineMove(self):movable_positons = self.Move()best_value = -99999for mov in movable_positons:self.chessboard[mov[0], mov[1]] = -1# 得到根节点每个选择的评价值val = self.AlphaBeta("man", MININF, MAXINF)#val = self.alpha_beta_valuation(-1, 1, MININF, MAXINF)# 将本次操作记录删掉self.chessboard[mov[0], mov[1]] = 0if best_value < val:best_value = valself.best_status = mov# max层def AlphaBeta(self, player, alpha, beta):# 当前可以下的位置movable_positons = self.Move()if (self.Winner() != "continue"):return self.Evaluate()if(player == "man"): # min层for mov in movable_positons:self.chessboard[mov[0]][mov[1]] = 1# Min层的beta = min(beta, 子结点的alpha)beta = min(beta, self.AlphaBeta("machine", alpha, beta))self.chessboard[mov[0]][mov[1]] = 0if alpha >= beta:return alphareturn betaelif(player == "machine"): # max层for mov in movable_positons:self.chessboard[mov[0]][mov[1]] = -1alpha = max(alpha, self.AlphaBeta("man", alpha, beta))self.chessboard[mov[0]][mov[1]] = 0# beta是父结点的alpha，即为max层结点的betaif alpha >= beta:return betareturn alpha# 计算棋子可落点def Move(self):positions = []for i in range(self.rows):for j in range(self.cols):if self.chessboard[i][j] == 0:positions.append((i, j))return positions# 计算出赢家，若步数=9仍未决出胜负，则平局def Winner(self):results = []# 遍历行for i in range(self.rows):results.append(np.sum(self.chessboard[i, : ]))# 遍历列for j in range(self.cols):results.append(np.sum(self.chessboard[: , j]))# 遍历对角线results.append(0)for i in range(self.rows):results[-1] += self.chessboard[i, i]results.append(0)for i in range(self.rows):results[-1] += self.chessboard[i, self.cols - i - 1]for result in results:if result == 3:return "man" # 玩家胜利elif result == -3:return "machine" # 机器胜利count = 0for i in range(self.rows):for j in range(self.cols):if self.chessboard[i][j] != 0:count += 1if count == self.cols * self.rows:return "tie"return "continue" # 游戏未结束# 打印棋盘def PrintBoard(self):for i in range(self.rows):for j in range(self.cols):if(self.chessboard[i][j] == -1):print("X", end=" ")elif(self.chessboard[i][j] == 1):print("O", end=' ')elif(self.chessboard[i][j] == 0):print("", end='_ ')print()# 判断落子位置是否合法def IsLegal(self, position):if(int(position[0]) >= self.rows or int(position[0]) < 0 or int(position[-1]) >= self.cols or int(position[-1]) < 0):return Falseelse:return True# 游戏的外部接口def Start(self):self.PrintBoard()while self.Winner() == "continue":if self.player == "machine":print("电脑玩家：")self.DetermineMove()self.machine_steps += 1self.chessboard[self.best_status[0]][self.best_status[1]] = -1self.player = "man"elif self.player == "man":while True:position = input("请输入下的位置坐标(行，列)：")if not self.IsLegal(position):print("该处不可以落子！")continueif self.chessboard[int(position[0])][int(position[-1])] == 0:self.chessboard[int(position[0])][int(position[-1])] = 1self.man_steps += 1self.player = "machine"breakelse:print("该位置已经有棋子了，请重新输入")self.PrintBoard()#self.best_status = ()if(self.Winner() == "man"):print("玩家胜利！")elif(self.Winner() == "machine"):print("电脑胜利！")if __name__ == '__main__':game = Chess()game.Start()