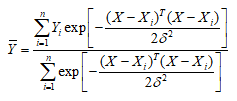组合总和（剪枝算法）

题目

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取

示例

示例 1：输入: candidates = [2,3,6,7], target = 7,
所求解集为:
[[7],[2,2,3]
]示例2：输入: candidates = [2,3,5], target = 8,
所求解集为:
[[2,2,2,2],[2,3,3],[3,5]
]

解题

思路

所谓剪枝算法，先考虑根节点为我们的目标值，也就是7
那么第二层，我们能减去的值为2，3，6，7，第二层的值就剩下5，4，1，0
我们见到了0，就假定这个枝叶已经开花了，纳入结果集，然后开始为第三层剪枝（5，4，1），减去的还是2，3，6，7
我们发现剪完之后很多叶子已经变成了负数，那么我们就把这个枝插给舍去
以此类推，所有为0的收入结果集，所有小于1的枝叶全部剪掉
最后即结果集。

代码

class Solution {public List<List<Integer>> combinationSum(int[] candidates, int target) {Arrays.sort(candidates);LinkedList<Integer> track = new LinkedList<>();combinationSum(candidates, 0, target, track);return result;}private List<List<Integer>> result = new ArrayList<>();private void combinationSum(int[] candidates, int start, int target, LinkedList<Integer> track) {if (target < 0) {return;} else if (target == 0) {result.add(new LinkedList<>(track));return;}for (int i = start; i < candidates.length; i++) {if (target < candidates[i]) {break;}track.add(candidates[i]);combinationSum(candidates, i, target - candidates[i], track);track.removeLast();}}
}

ps：代码看着简单，实则要考虑的点不少：

1. 为什么获取结果集要用result.add(new LinkedList<>(track));而不是直接add(track);
   所有递归保存结果的均未track如果result里面所有的引用都指向它，最后的结果集里面的数据都是一样的，所以要重新创建集合。
2. 为什么每次递归回来要track.removeLast();
   因为在剪枝的时候所有的节点都放到了track里面，当track判断完毕后不行被剪枝，还保留不行的叶子的话，结果集会多出很多垃圾的节点
3. 参数start是做什么用的
   以3为二层节点的树是不能用2节点的，因为2节点一定已经把这种情况给包含了，所以不引如start结果集会重复

回溯算法的公式

1、路径：也就是已经做出的选择。2、选择列表：也就是你当前可以做的选择。3、结束条件：也就是到达决策树底层，无法再做选择的条件。result = []
def backtrack(路径, 选择列表):if 满足结束条件:result.add(路径)returnfor 选择 in 选择列表:做选择backtrack(路径, 选择列表)撤销选择