人工智能之AlphaBeta剪枝算法

任务描述

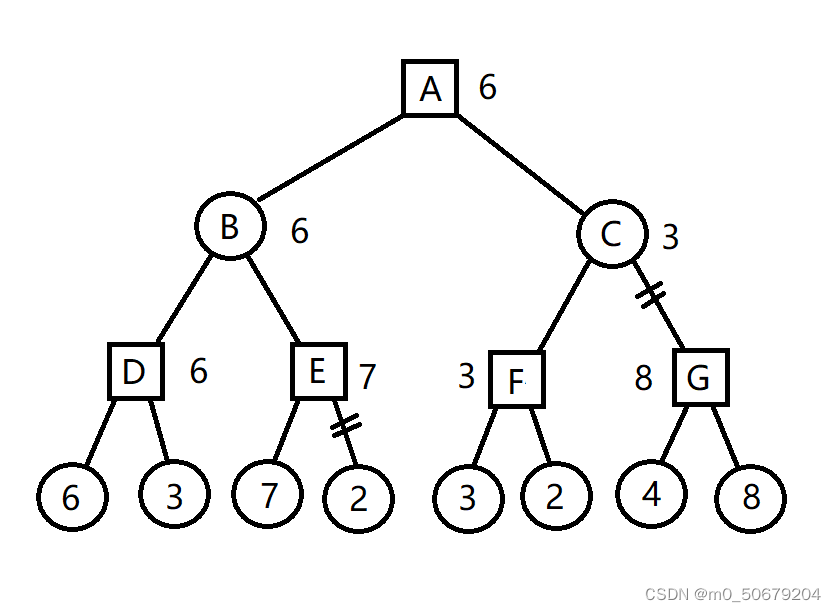
本关任务：学习人工智能博弈算法中的 AlphaBeta 剪枝技巧，并基于 MinMax 算法编程实现如下图博弈树最优值问题的求解。
在这里插入图片描述
博弈树的输入形式为字符串：[A, [B, (E, 3), (F, 12), (G, 8)], [C, (H, 2), (I, 4), (J, 6)], [D, (K, 14), (L, 5), (M, 2)]]，其中 [] 里的第一项为结点名称，后面的 [] 或 () 为子结点，而 () 里边则为叶子结点名称及其值。通过 Python 中的 ast.literal_eval 模块可以将该字符串数据解析为数据在 Python 数据类型里本应该存在的形式，在本例子中即为列表和元组，使用方法可见文件目录中的 testAlphaBeta.py 文件。

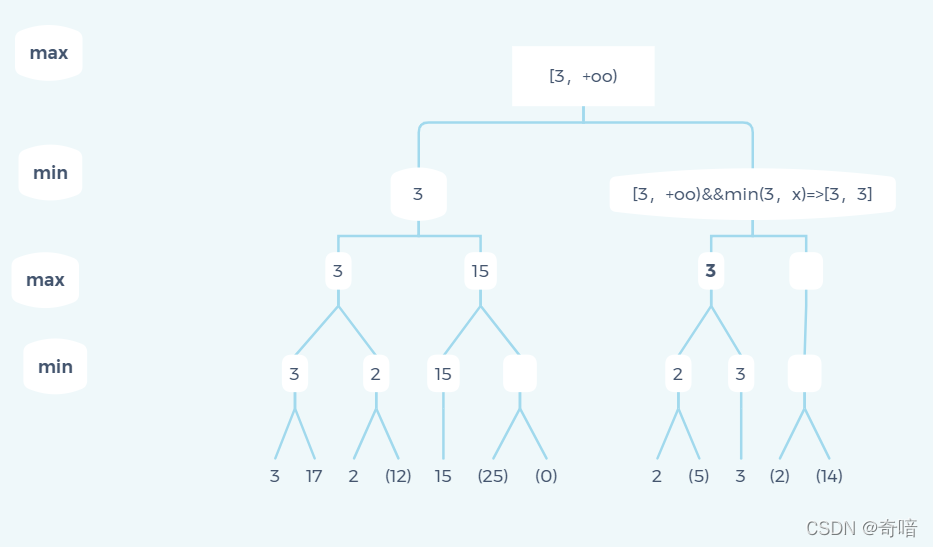
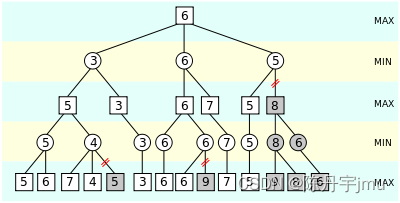
学员需要将列表和元组组成的数据构建成一棵如上图所示的博弈树，然后求解最优值，该博弈树的根结点为 Max 层，上图所示的最优结点为 B ，最优值为 3 。

相关知识

为了完成本关任务，你需要掌握：1. alpha-beta 剪枝原理，2.问题求解思路。

alpha-beta 剪枝原理

极小极大值算法必须检查博弈树的全部结点，也就是游戏的全部状态，显然，搜索时间是指数级增长的。虽然我们无法消除指数级的运算规模，但是可以通过一些剪枝策略有效地将其减半，换言之，可能不需要遍历博弈树中每一个结点就可以计算出正确的极小极大值，αβ剪枝 Alpha-Beta 就是其中的一种。
αβ剪枝会减掉那些不可能影响决策的分支，最后返回和极小极大值算法同样的结果。上图的博弈树用αβ剪枝过程表达如下，每个结点上面标出了可能的取值范围，B下面的第一个叶子结点为3，剩余两个结点分别为12和8，因此B的取值范围更新为[3,3]，现在由此可以推断根结点A的取值范围为[3,+∞)。然后结点C下面的第一个叶子结点为2，因此C这个 MIN 结点的值最多为2，而又已知根结点A的最低取值为3，所以结点C的余下后继结点无需再考虑，这就是αβ剪枝的一个具体实例。余下的博弈树按照之前的思想逐步更新结点的取值范围，减掉不可能影响根结点取值的分支。
在这里插入图片描述
将上述过程用 MINMAX 公式化表达如下：

其中结点C的两个没有计算的结点的值分别为x和y，即可以得出根结点的值以及因此做出的极小极大决策与被减掉的叶节点x和y无关。

极小极大搜索时深度优先的，所以在任何时候都只需考虑树中某一路径上的结点，αβ剪枝的名称取自描述这条路径上的回传值的两个的参数：

α：到目前为止路径上发现的 MAX 的最佳选择（即极大值）

β：到目前为止路径上发现的 MIN 的最佳选择（即极小值）

αβ剪枝策略在搜索中不断更新α和β的值，并且当某个结点的值分别比目前的 MAX 的α或者 MIN 的β值更差的时候，减掉此结点剩下的分支（即终止递归搜索），完整算法的伪代码如下图所示：
在这里插入图片描述

问题求解思路

详细分析输入数据与博弈树的对应关系，使用递归的方法创建一棵博弈树，然后按照以上描述的剪枝过程完成以下各个函数功能，最终完成博弈树的最优值求解问题。

编程要求

本关的编程任务是补全右侧代码片段 buildTree 、minmax_with_alphabeta 、max_value 、min_value 、get_value 和 isTerminal 中 Begin 至 End 中间的代码，具体要求如下：

在 buildTree 中，以递归的方式创建一棵博弈树，初始传入参数为博弈树的根结点 root ，以及解析后的列表与元组的组合数据 data_list；

在 minmax_with_alphabeta 中，基于 AlphaBeta 剪枝思想实现 MinMax 算法主体部分，初始传入参数为博弈树的根结点，函数最后返回根结点的最优决策结点；

在 max_value 中，计算该博弈树结点的子结点中的最大的评估值，并返回，传入参数为结点以及 Alpha 和 Beta 区间上下限；

在 min_value 中，计算该博弈树结点的子结点中的最小的评估值，并返回，传入参数为结点以及 Alpha 和 Beta 区间上下限；

在 get_value 中，返回结点 node 的值，即为 node.val；

在 isTerminal 中，判断某结点是否为最终结点（叶子结点），也就是说是否有子结点。

测试说明

平台将自动编译补全后的代码，并生成若干组测试数据，接着根据程序的输出判断程序是否正确。

以下是平台的测试样例：

测试输入：
[A, [B, (E, 3), (F, 12), (G, 8)], [C, (H, 2), (I, 4), (J, 6)], [D, (K, 14), (L, 5), (M, 2)]]
预期输出：
B 3

代码

# -*- coding:utf-8 -*-import copy     # 注意对象的深拷贝和浅拷贝的使用！！！
from ast import literal_evalclass GameNode:'''博弈树结点数据结构成员变量：name - string 结点名字val - int  结点值children - list[GameNode] 子结点列表'''def __init__(self, name='', val=0):self.name = name        # charself.val = val          # intself.children = []      # list of nodesclass GameTree:'''博弈树结点数据结构成员变量：root - GameNode 博弈树根结点成员函数：buildTree - 创建博弈树'''def __init__(self):self.root = None                # GameNode 博弈树根结点def buildTree(self, data_list, root):'''递归法创建博弈树参数：data_list - list[] like this ['A', ['B', ('E', 3), ('F', 12)], ['C', ('H', 2)], ['D', ('K', 14)]]root - GameNode'''#请在这里补充代码，完成本关任务#********** Begin **********#for i in range(1,len(data_list)):if type(data_list[i]) == list:root.children.append(GameNode(data_list[i][0]))self.buildTree(data_list[i],root.children[i-1])else:root.children.append(GameNode(data_list[i][0],data_list[i][1]))#********** End **********#class AlphaBeta:'''博弈树结点数据结构成员变量：game_tree - GameTree 博弈树成员函数：minmax_with_alphabeta - 带AlphaBeta剪枝的极大极小值算法，计算最优行动max_value - 计算最大值min_value - 计算最小值get_value - 返回结点的值isTerminal - 判断某结点是否为最终结点'''def __init__(self, game_tree):self.game_tree = game_tree      # GameTree 博弈树def minmax_with_alphabeta(self, node):'''带AlphaBeta剪枝的极大极小值算法，计算最优行动参数：node - GameNode 博弈树结点返回值：clf - GameNode 最优行动的结点'''#请在这里补充代码，完成本关任务#********** Begin **********#clf = self.max_value(node,-10000,10000)for child in node.children:if child.val == clf:return child;#********** End **********#def max_value(self, node, alpha, beta):'''计算最大值参数：node - GameNode 博弈树结点alpha - int 剪枝区间下限值beta - int 剪枝区间上限值返回值：clf - int 子结点中的最大的评估值'''#请在这里补充代码，完成本关任务#********** Begin **********#if self.isTerminal(node):return self.get_value(node)clf = -10000for child in node.children:clf = max(clf,self.min_value(child,alpha,beta))if clf >= beta:return clfalpha = max(alpha,clf)node.val = clf;return clf#********** End **********#def min_value(self, node, alpha, beta):'''计算最小值参数：node - GameNode 博弈树结点alpha - int 剪枝区间下限值beta - int 剪枝区间上限值返回值：clf - int 子结点中的最小的评估值'''#请在这里补充代码，完成本关任务#********** Begin **********#if self.isTerminal(node):return self.get_value(node)clf = 10000for child in node.children:clf = min(clf,self.max_value(child,alpha,beta))if clf <= alpha:return clfbeta = min(clf,beta)node.val = clf;return clf;#********** End **********#def get_value(self, node):'''返回结点的值参数：node - GameNode 博弈树结点返回值：clf - int 结点的值，即 node.val'''#请在这里补充代码，完成本关任务#********** Begin **********#return node.val;#********** End **********#def isTerminal(self, node):'''判断某结点是否为最终结点（无子结点）参数：node - GameNode 博弈树结点返回值：clf - bool 是最终状态，返回True，否则返回False'''#请在这里补充代码，完成本关任务#********** Begin **********#if node.val == 0:return Falseelse:return True#********** End **********#