在写之前首先感谢：https://blog.csdn.net/wenjianmuran/article/details/90633418

这里主要介绍minmax算法和α-β剪枝,相当于对一下文章的翻译：

α-β剪枝

Minmax算法

正文：

看了很多关于α-β剪枝算法，大致明白了其中的含义，但有一个事情总是弄不明白，就是如何在一个状态下，决定采用那个分支进行搜索。我把对于上述两个英文链接的理解说下。

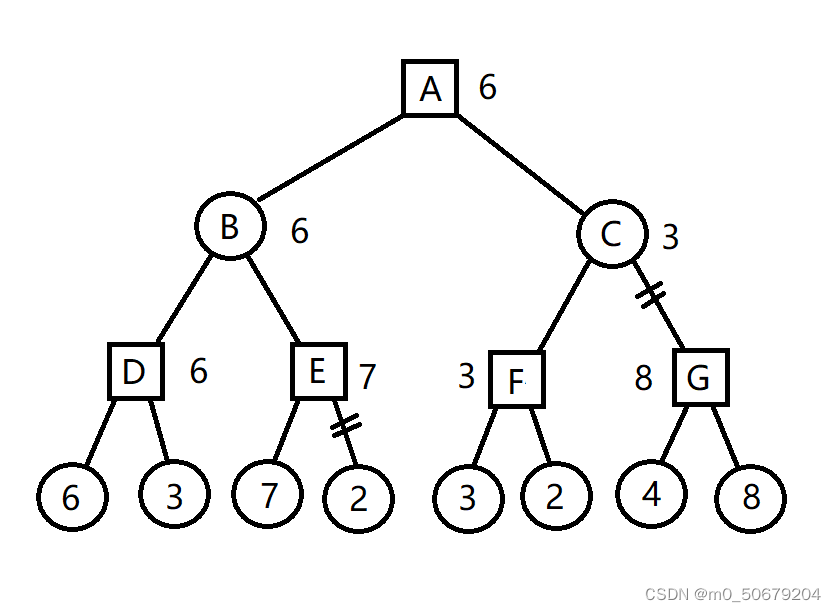
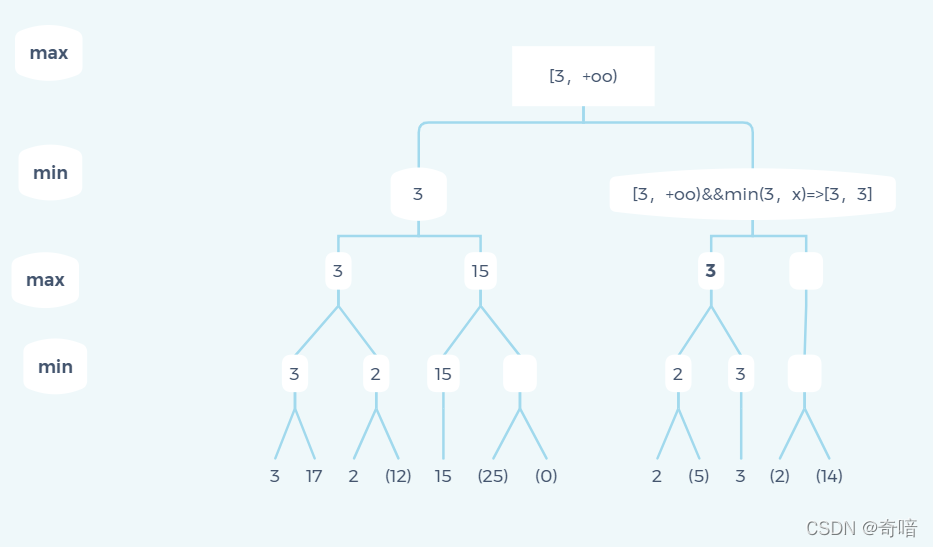
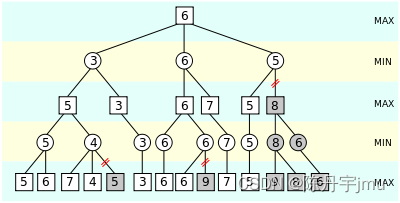
（一）α-β剪枝算法是深度优先搜索算法，深度优先就是先尽可能进行一个子节点的不断深度扩展，不考虑其它子节点。如果画图就像下面这样（图来自：http://web.cs.ucla.edu/~rosen/161/notes/alphabeta.html 以下不特殊说明，图形均来自该链接）

（二）搜索树上的每个节点都有一个评估值，如果用方形表示自己方现在的状态，上图中每一个连线都相当于从一个状态到另一个状态的转变，比如棋类比赛，一个连线就相当于走一步棋。

（三）搜索过程中为了减少搜索时间，对于每个节点的评估值设置一个上界β和下界α，搜索过程中更改上界和下界，使得他们决定的区间足够小，这样我们就可以更精确的定界。也就是说，搜索过程其实是不断减少上界和增加下界，用图像表示就是：、

开始的上界β和下界α

随着搜索进行，他们的变化可能是（注意a在增加，β在减少）：

（四）己方和对方都足够聪明，己方采用最有利于己方的着法（就是采用那个分支），由于评估值的存在，己方倾向于取最大的评估值走法。所以对于方型节点（我方）称为Max节点，如果它的所有子节点都已经有明确的评估值，它的评估值是其所有子节点评估值的最大值。对方采取的走法必然是抑制我方的走法，就是对方要采用所有可能走法的最小评估值走法，所以对于对方节点（圆形节点）称为Min节点，如果它的所有子节点都已经有明确的评估值，它的评估值是其所有子节点评估值的最小值。

这里注意，一个节点想知道自己的评估值，是通过其子节点的评估值来确定的。当其所有子节点都具有评估值时，根据这个节点的类型（Max或Min），就可以直接计算出这个节点的评估值。

如果把搜索树全部扩展就是Max-Min算法。但全部扩展是不合算的，就产生了α-β剪枝算法。关于Max-Min算法参考：http://web.cs.ucla.edu/~rosen/161/notes/minimax.html

（五）对于一个当前状态，如何进行计算呢。

第一：决定深度搜索几层，也就是向下扩展几层子节点。节点当前层不算，下图是深度搜索4层。最开始时最上层节点（就是我们当前准备计算或所在的节点状态），这个节点的评估值我们是不知道的，但我们可以设置一个上界和下界，就像图中标注的那样，下界定于负无穷，上界定与正无穷。它是己方节点（方形），它走一步，到下面的圆形节点，此时就该对方走一步，对方处于圆形节点中。圆形节点的上界和下界直接复制其父（图中是顶层方形）节点的上下界。对方节点再，扩展一个子节点（注意不论是我方还是对方一次只向深度方向扩展一个子节点，这是深度搜索的精髓），来到图中从上数第二个方形节点。这样构成一个回合（full move）

第二：当到达指定的回合数比如2回合，就是4层时。此时我们就可以根据预设的静态评估函数计算方法，计算出最后这个节点的评估值。注意：这个评估值是直接算出来的，不是通过搜索得到的，在图中对应的就是最小面的方形的评估值3.

也许会有这样的疑惑，既然评估函数可以直接算出，为什么不直接算，还要构造搜索树呢。我的理解是这个评估函数本身是启发式的，对于结束的状态它是合理的，对于中间状态它并不合理。如果对于一个状态，我们采用宽度优先，并按照静态方法计算其所有子节点的评估值，然后采用最大或最小策略进行分支决定，这就是贪婪算法。

第三：计算出叶节点（图中方形框中3）的评估值，就可以利用它来估计其父节点（圆形节点）的上下界。由于圆形节点是最小值节点，就是说该圆形节点的评估值应该是它所有子节点（可能有很多，由于深度优先，我们现在只得到了一个，就是图中最底层那个方形，评估值为3）评估值中的最小值。现在圆形节点有一个评估值是3子节点，那么圆形节点的最大值不应该大于这个3，就是说对于圆形节点，可以更新它的上界值，β=3，如图：

扩展圆形节点的另外子节点，并直接计算评估值，如果有评估值小于3的就更新这个β，否则保留这个β，示例中另一个节点是17，所以没有更新β

第四：现在对于圆形节点A它的所有子节点都已经得到评估值，那么它的评估值可以直接按照它本身的类型得到了。由于它是Min节点，所以圆形节点具有3的评估值，A的父节点是B,B是最大值节点，就是说B的评估值是其所有子节点中最大的那个值，现在我们已经得到它的一个子节点A，具有评估值3，所以B最少取得3的评估值，就是B评估值下界是3，即B节点中a=3，如图：

第五：现在我们还计算不了B的评估值，因为它的子节点没有完全得到。扩展B形成其它子节点C，C继承B的门限值，如图：

C没有达到规定层，继续扩展C，得到子节点D ，如图：

计算D的评估值，假设是2.按照上面第一步类似的计算可以得到C的上界为2，即β=2，对于节点C而言，它的下界大于它的上界，这是不合理的，所以C的其它节点不用考虑了。把C的评估值赋值成违背规则的那个数，这里是2，如图：

第六：现在对于B而言，假设没有其它子节点（如果有按照类似扩展C的方式进行），现在B可以计算评估值，按照它的最大值特性，它具有评估值3，类似前面的计算它的父节点的beta值为3，如图：

第七：继续向上逆推

。。。。。。。。。。。。。。。。

规律：

（1）一个具有评估值节点如果其父节点是最小值节点，那么这个节点可以更新它父节点的beta值，就是上界值

（2）一个具有评估值节点如果其父节点是最大值节点，那么这个节点可以更新它父节点的alpha值，就是下界值

（3）父节点进行扩展子节点时，子节点携带父节点的上下界值

（4）节点的所有子节点都被计算得到评估值，该节点可以按照这个节点类型计算出评估值

（5）每次都要到达指定的层次才开始逆推计算得到各层节点的上下界值和评估值

（6）上界值一定大于下界值，否则剪枝。被剪枝的节点评估值，是最后计算得到的违背规则的那个数值（alpha或beta)

其它过程请看：http://web.cs.ucla.edu/~rosen/161/notes/alphabeta.html