前言

先做了一版五子棋的小项目，后面又做了一个功能更强大的中国象棋的项目，但是始终都没有实现一版“智能”AI。
明知道这类博弈问题的ai算法底层都是使用极大极小搜索算法和α-β剪枝剪枝优化，但是尝试过好多次都没能拿下它。。。。
网上关于这类算法的博客文章层出不穷，但是基本上是讲得非常抽象，然后再给个伪代码，重点的思路流程一带而过，感觉说了很多，但是实际上却又什么都没说什么都没讲明白，好不容易找到一篇讲清楚流程的文章，但是人家也仅仅只是讲了思路流程。
要知道，像这种难顶的算法，哪怕知道了流程思路，还真不一定能写得出代码啊。
真的是为了搞懂这个算法，人都找麻了。。。

吐糟归吐槽，也算是黄天不负有心人，看了十几篇文章，总算是把两个算法的思想以及代码实现都拿下了。
这两种算法的基本背景和内容相信大家都知道一二，我就不做讲述了，下面我就带领大家直奔主题。

minimax算法

这次我就不按照往常的方式进行讲述，先直接给出代码，如果你能够完全看懂，那就可以直接跳过这节的内容，毕竟自己理解肯定比别人带着自己理解所得到的效果会更好。

完整代码

const minimax = (player, node) => {if (!node.value) {const map = [];node.children.forEach(child => {map.push(minimax(player ^ 1, child));});node.value = player === 1 ? Math.max(...map) : Math.min(...map);}return node.value;
}

你没看错，极大极小搜索算法就只有几行代码。
如果这几行代码你不能理解，那么接下来就让我带着你理解。

算法思想

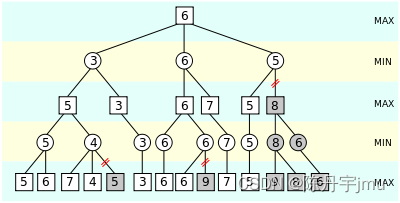
首先先看一个实际问题：
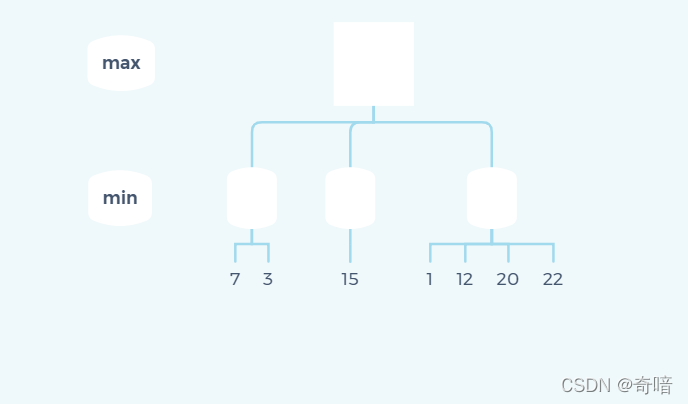
在这里插入图片描述
如上图所示，求最终max的结果。

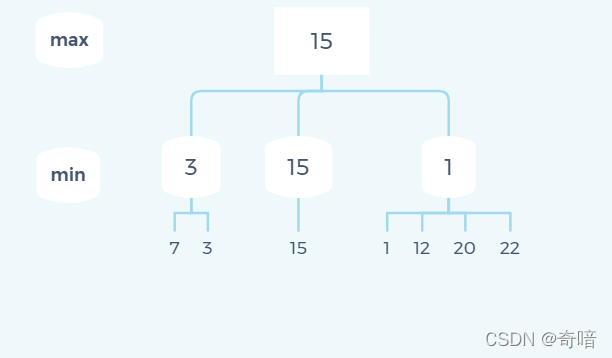
不难得到，最终的求解流程就是如上图所示，结果就是15.
在奇数层找最大结果，在偶数层找最小结果，这就是极大极小搜索的核心思想。
极大极小搜索就是在当前层我肯定寻找对自己最有利的结果，那么再下一轮搜索中对方肯定也会寻找对他而言最有利的结果（也就是对自己最无力的结果），从而最终得到的结果就是对于双方最有利的结果。

代码实现

接来下就以这个例题来看看代码的实现：

// 1:max  0:min
const minimax = (player, node) => {// 如果不是底层则继续递归所有子元素if (!node.value) {const map = [];//收集当前层的所有结果node.children.forEach(child => {map.push(minimax(player ^ 1, child));});// 根据当前player来确定进行max或者min操作node.value = player === 1 ? Math.max(...map) : Math.min(...map);}// 子元素的结果返回给父元素return node.value;
}
function main(tree) {const res = minimax(1, tree);console.log(res);console.log(tree);
}
const tree1 = {value: null,children: [{value: null,children: [{value: 7,children: []},{value: 3,children: []}]},{value: null,children: [{value: 15,children: []}]},{value: null,children: [{value: 1,children: []},{value: 12,children: []},{value: 20,children: []},{value: 22,children: []}]},]
}
main(tree1);

运行上述代码，我们就可以得到预期的极大极小搜索结果以及完整的搜索树。
其实极大极小搜索是一种类似于回溯的递归思路，只不过每层我们只保留一个结果，而结果的保留方式取决于当前层次的奇偶性。
通过上述算法思路和代码注释，相信这次你应该能够完全掌握极大极小算法。

算法优化

还是看上述的那个案例，细心点我们不难发现，当我们在第三个分支第三的1时，其实就没必要在继续遍历后续的12、20以及22这三个节点。因为其上一层是min层，那么其结果必然不会超过1，而同层次已经有节点为15，所以当前这条分支就完全可以进行剪枝操作，而这种优化的思想也就是α-β剪枝算法。

α-β剪枝算法

完整代码

同样，我也先给出完整代码，大家先尝试是否能够自己理解。

const alphaBeta = (player, node, alpha, beta) => {if (!node.value) {const map = [];for (let i = 0; i < node.children.length; i++) {const val = alphaBeta(player ^ 1, node.children[i], alpha, beta);map.push(val);if (player === 1) {if (val > alpha) {alpha = val;}if (alpha >= beta) {return alpha;}} else {if (val < beta) {beta = val;}if (alpha >= beta) {return beta;}}}node.value = player === 1 ? Math.max(...map) : Math.min(...map);}return node.value;
}

你没看错，在极大极小搜索的基础下得到优化后的α-β剪枝算法仅仅只是多了几行逻辑代码。
但是就是这几行代码，使得其理解难度和基础的极大极小搜索已经不在一个层次上。

算法思想

α-β剪枝算法的思想其实在极大极小算法的优化部分已经提到，但是那里描述的不完整。
现在我尝试就我自己的理解对其进行完整的描述：
极大极小搜索是一种dfs递归遍历的思想，最终的目的也只是为了获取最上层的那个结果。所以我们不妨先默认给最上层结果一个初始的区间范围，即(α，β)（一般是负无穷到正无穷），然后我们每递归遍历完一条分支的时候根据反馈的结果都会相应更新这个区间范围，并把此区间范围带入后续分支的递归中。如果后续分支的子分支得到的结果不满足这个区间，那么就完全可以放弃继续递归遍历这整条分支，即α-β剪枝。
这里的难点在于节点间其(α，β)的变化，下面就举几个具体的案例。

案例一：还是上述那个例子，只是这次是使用α-β剪枝算法的思路
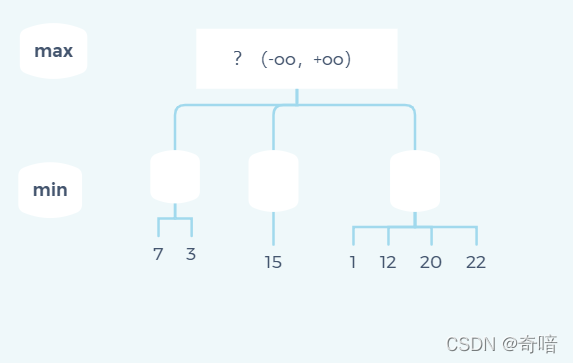
在这里插入图片描述

首先，当我们在min层第一个节点得到结果7，会得到下面的一个状态图：
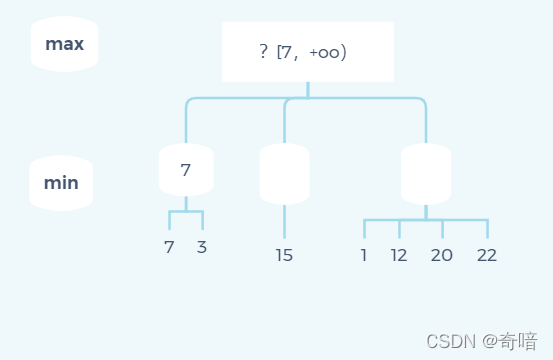
在这里插入图片描述
即通过第一条分支我们能够确定下界α为7，同理递归遍历第二个节点时我们得到下面这张状态图：

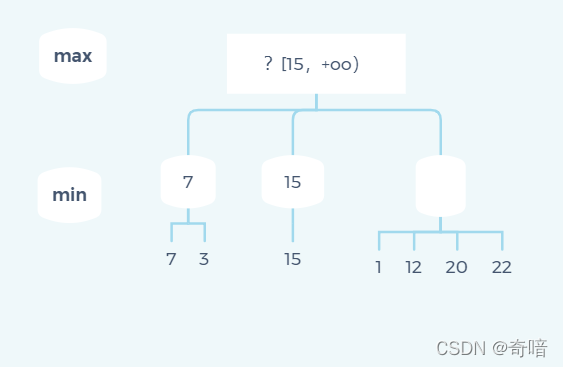
上面这一切都挺正常，现在遍历到第三个节点的第一个子节点1时，就可以终止遍历第三个节点了。
可以看下面这张状态图：（括起来的数字代码当前分支被剪枝）
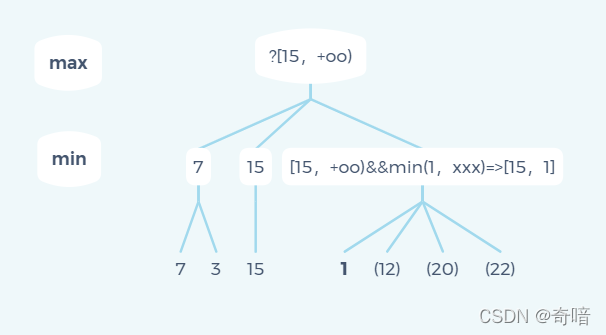
在这里插入图片描述

父元素通知它的下界α要大于15，但是自己得到其中一个为子结果1，即注定了当前节点的上界为1，下界15大于上界1，所以当前节点完全可以放弃，即无需再继续遍历后续子节点的值，瞬间就减少了三条子分支的遍历。

是不是找到点感觉了，但是这个示例太简单了，不得劲，那么下面就换一个复杂一点的例子：
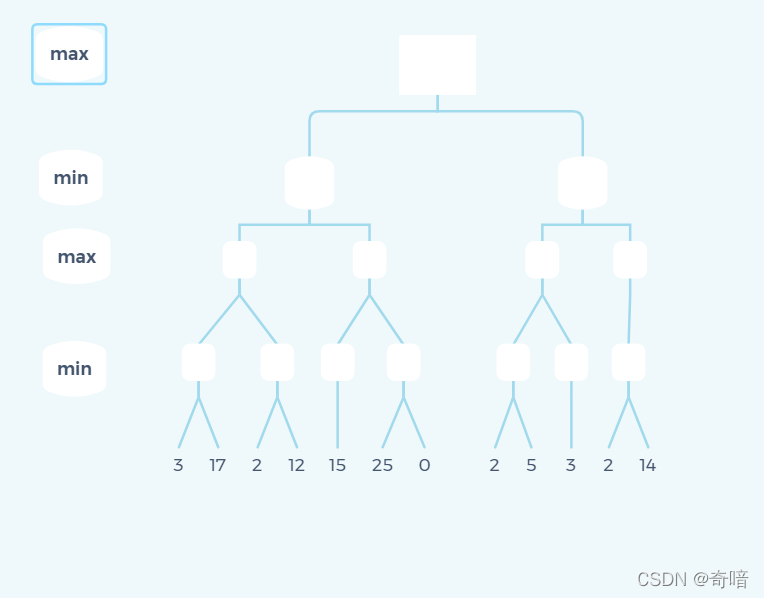
在这里插入图片描述
这个案例就显得复杂多，大家先试着自己思考一下，这次我就不把所以细节状态都展示出来，我只把产生剪枝时的状态展现出来。

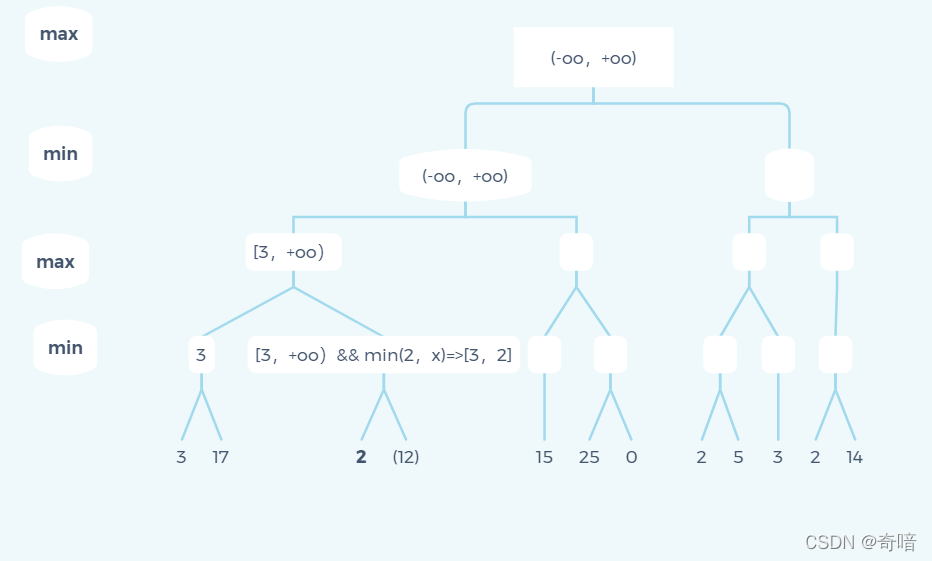
第一个会进行剪枝的地方是遍历完图中的2时，其父节点会产生[3,2]一种下界大于上界的情形，所以后面的12子节点被剪枝。
同样被剪枝的还有三个地方：
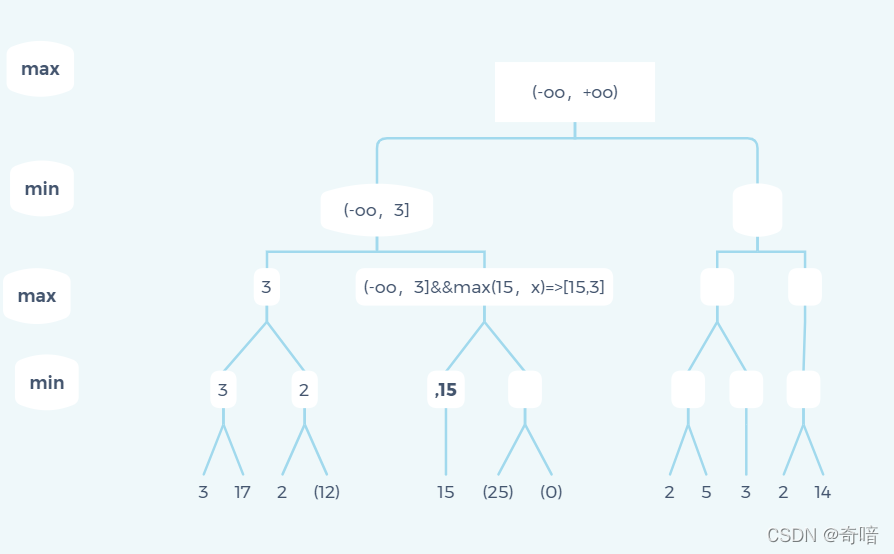
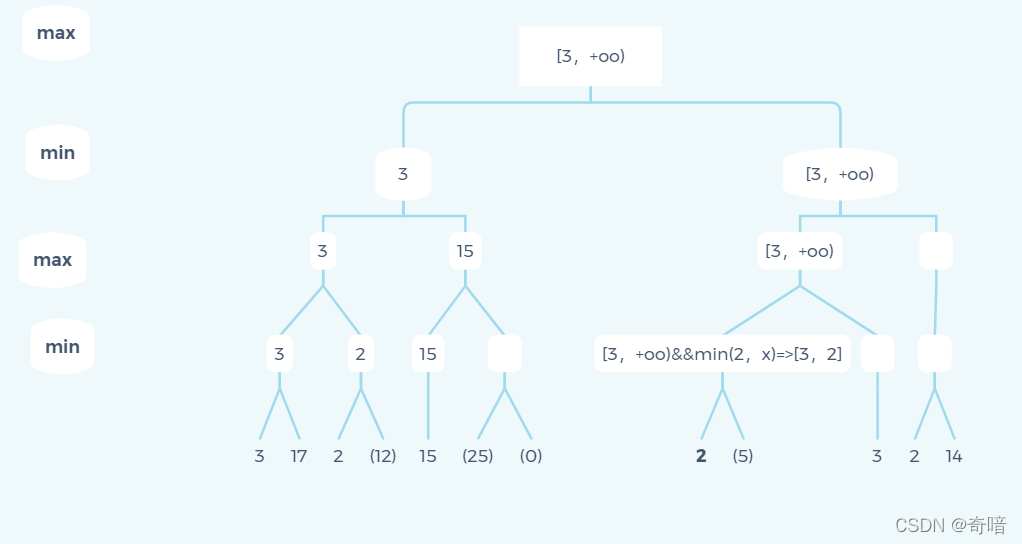
在这里插入图片描述

在这里插入图片描述

可能会有些朋友对这张图另一个分支[3，+oo)这个状态为什么能一直传递给子元素会有疑惑，这里我解释一下：
在第一个大分支已经得到结果3，那么在另一个分支里面如果有任何小于3的数据的分支不管是在max层还是min层，这条分支其实都是无用分支（这个地方大家可以仔细理解理解）。

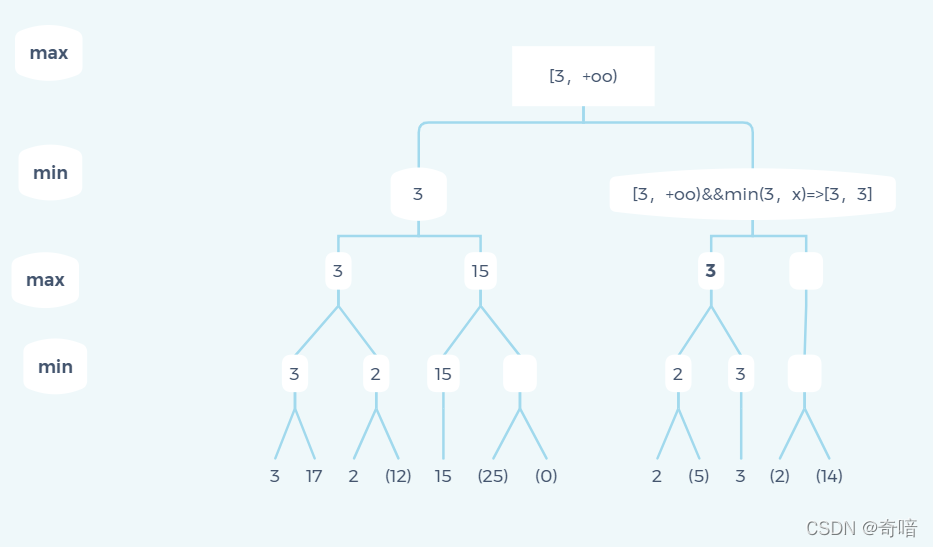
在这里插入图片描述
最后一个地方，得到上界等于下界，那么后面的分支也无需遍历了，因为当前节点能返回的值要么就是这个定值要么就是无解。
通过以上几个案例，我们不难发现α-β剪枝的核心在于通过递归更新节点的上界和下界从而实现剪枝的效果。
具体可以总结为以下四点：

max层子元素的值大于当前下界的值更新下界
max层下界大于等于上界直接返回下界（返回较大者），即剪枝
min层子元素的值小于当前上界的值更新上界
min层下界大于等于上界直接返回上界（返回较小者），即剪枝

代码实现

在极大极小搜索算法的基础上，结合上述四点α-β剪枝的核心，即可得到下面的代码：

//[alpha,beta]
const alphaBeta = (player, node, alpha, beta) => {if (!node.value) {const map = [];for (let i = 0; i < node.children.length; i++) {const val = alphaBeta(player ^ 1, node.children[i], alpha, beta);map.push(val);// 上次子元素的结果更改父元素的alpha beta，并将更新后的alpha beta带入到后续子元素的递归中if (player === 1) {// max层 子元素的值大于当前下界的值 更新下界if (val > alpha) {alpha = val;}// max层 下界大于等于上界直接返回下界（返回较大者）if (alpha >= beta) {return alpha;}} else {// min层 子元素的值小于当前上界的值 更新上界if (val < beta) {beta = val;}// min层 下界大于等于上界直接返回上界（返回较小者）if (alpha >= beta) {return beta;}}}// 返回当前层节点的极值，便于父元素进行剪枝（并不是返回alpha或者beta）node.value = player === 1 ? Math.max(...map) : Math.min(...map);}return node.value;
}function main(tree) {const res = alphaBeta(1, tree, Number.MIN_SAFE_INTEGER, Number.MAX_SAFE_INTEGER);// Number.MIN_VALUE进行直接比较大小时有bugconsole.log(res);console.log(tree);
}const tree1 = {value: null,children: [{value: null,children: [{value: 7,children: []},{value: 3,children: []}]},{value: null,children: [{value: 15,children: []}]},{value: null,children: [{value: 1,children: []},{value: 12,children: []},{value: 20,children: []},{value: 22,children: []}]},]
}
main(tree1);

运行此代码，能得到和极大极小搜索算法同样的结果。

算法对比

接下来，我稍微将两个算法补充点东西，让算法的优化效果展现得更加明显。

let countMinimax = 0;
let countAlphaBeta = 0;
// 1:max  0:min
const minimax = (player, node) => {countMinimax++;// 如果不是底层则继续递归所有子元素if (!node.value) {const map = [];//收集当前层的所有结果node.children.forEach(child => {map.push(minimax(player ^ 1, child));});// 根据当前player来确定进行max或者min操作node.value = player === 1 ? Math.max(...map) : Math.min(...map);}// 子元素的结果返回给父元素return node.value;
}//[alpha,beta]
const alphaBeta = (player, node, alpha, beta) => {countAlphaBeta++;if (!node.value) {const map = [];for (let i = 0; i < node.children.length; i++) {const val = alphaBeta(player ^ 1, node.children[i], alpha, beta);map.push(val);// 上次子元素的结果更改父元素的alpha beta，并将更新后的alpha beta带入到后续子元素的递归中if (player === 1) {// max层 子元素的值大于当前下界的值 更新下界if (val > alpha) {alpha = val;}// max层 下界大于等于上界直接返回下界（返回较大者）if (alpha >= beta) {node.value = 'A' + alpha;return alpha;}} else {// min层 子元素的值小于当前上界的值 更新上界if (val < beta) {beta = val;}// min层 下界大于等于上界直接返回上界（返回较小者）if (alpha >= beta) {node.value = 'B' + beta;return beta;}}}// 返回当前层节点的极值，便于父元素进行剪枝（并不是返回alpha或者beta）node.value = player === 1 ? Math.max(...map) : Math.min(...map);}return node.value;
}function main(tree) {const res = minimax(1, tree);//const res = alphaBeta(1, tree, Number.MIN_SAFE_INTEGER, Number.MAX_SAFE_INTEGER);console.log(countMinimax);//console.log(countAlphaBeta);
}// 11 8
const tree1 = {value: null,children: [{value: null,children: [{value: 7,children: []},{value: 3,children: []}]},{value: null,children: [{value: 15,children: []}]},{value: null,children: [{value: 1,children: []},{value: 12,children: []},{value: 20,children: []},{value: 22,children: []}]},]
}

首先，定义两个全局变量countMinimax和countAlphaBeta分别记录极大极小搜索算法和α-β剪枝算法的遍历次数，并且在α-β剪枝算法进行剪枝的地方重置的节点的value值使得剪枝处更一目了然。
再次分别使用minimax和alphaBeta对Tree1进行操作，分别得到11和8两个结果，和预期一样，少遍历了三次，即减掉了三个叶子节点。

结语

到此，相信大家应该都能够掌握极大极小搜索算法和α-β剪枝算法，本篇文章使用的语言是javascript，主要是使用javascript来描述具体示例会更加方便。有了这两大算法作为基石，中国象棋以及五子棋的ai之路也便有了希望。
最后，如果大家对于本篇文章有任何疑问的地方，欢迎评论区留言或者私信我，我会积极给与答复。希望这篇文章的内容能够解决你们的疑惑，下期再会！