文章目录
- 等可能概型(古典概型)
等可能概型(古典概型)
定义:若实验满足:
- 样本空间 S 种样本点有限(有限性)
- 出现每一个样本点的概率相等(等可能性)
称这种试验为等可能概型(或古典概型)
P ( A ) = A 所 包 含 的 样 本 点 数 S 中 的 样 本 点 数 P(A) = \frac{A所包含的样本点数}{S中的样本点数} P(A)=S中的样本点数A所包含的样本点数
例 1: 一袋中有5个球,其中3个为白球,2个为蓝球,设取到每一球的可能性相等.
(1)从袋中随机取一球,记A={ 取到白球 },求P(A).
(2)从袋中不放回取两球,记B={两个都是白球},求
P(B).
先说明下抽样方法:
不放回抽样: 第 1 次取出一个球,记录其颜色,不再放回,第 2 次从剩余的球中取出一球;
放回抽样: 第 1 次取出一个球,记录其颜色,放回,第 2 次依然从全部的球中取出一球.
解: 将球编号,白球为 1,2,3,蓝球为 4,5.
(1) S = { 1 , 2 , 3 , 4 , 5 } , A = { 1 , 2 , 3 } ⟹ P ( A ) = 3 5 S = \{1,2,3,4,5\}, A = \{1,2,3\}\implies P(A) = \frac{3}{5} S={1,2,3,4,5},A={1,2,3}⟹P(A)=53
(2) S = { ( 1 , 2 ) , ( 1 , 3 ) , . . . ( 5 , 3 ) , ( 5 , 4 ) } , S = \{(1,2),(1,3),...(5,3),(5,4)\}, S={(1,2),(1,3),...(5,3),(5,4)},
B = { ( 1 , 2 ) , ( 1 , 3 ) , ( 2 , 1 ) , ( 2 , 3 ) , ( 3 , 1 ) , ( 3 , 2 ) } . B=\{(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)\}. B={(1,2),(1,3),(2,1),(2,3),(3,1),(3,2)}.
S S S 所包含的样本点数是 5x4
A A A 所包含的样本点数是 3x2
P ( B ) = 3 × 2 5 × 4 = C 3 2 C 5 2 = 0.3 P(B) = \frac{3\times 2}{5\times 4} = \frac{C_{3}^{2}}{C_{5}^{2}} = 0.3 P(B)=5×43×2=C52C32=0.3
一般地,如果有 N N N 个球,其中 a a a 个白球, b = N − a b = N - a b=N−a 个蓝球采用不放回抽样取n个球( n ≤ N n\leq N n≤N),记 A k = { 恰 好 取 到 k 个 白 球 } ( k ≤ a ) A_k=\{恰好取到k个白球\} (k\leq a) Ak={恰好取到k个白球}(k≤a),则
P ( A k ) = C a k C b n − k C N n , 其 中 C N n = ( N n ) = N ! n ! ( N − n ) ! P(A_k) = \frac{C_{a}^{k}C_{b}^{n-k}}{C_{N}^{n}},其中 C_{N}^{n} = \tbinom{N}{n} = \frac{N!}{n!(N-n)!} P(Ak)=CNnCakCbn−k,其中CNn=(nN)=n!(N−n)!N!
P ( A 0 ) = C a 0 C b n C N n , P ( A 1 ) = C a 1 C b n − 1 C N n , P ( A 2 ) = C a 2 C b n − 2 C N n P(A_0) = \frac{C_{a}^{0}C_{b}^{n}}{C_N^{n}},P(A_1) = \frac{C_{a}^{1}C_{b}^{n-1}}{C_N^{n}},P(A_2) = \frac{C_{a}^{2}C_{b}^{n-2}}{C_N^{n}} P(A0)=CNnCa0Cbn,P(A1)=CNnCa1Cbn−1,P(A2)=CNnCa2Cbn−2
P ( 至 少 取 到 2 个 白 球 ) = 1 − P ( A 0 ) − P ( A 1 ) P(至少取到 2 个白球) = 1 - P(A_0) - P(A_1) P(至少取到2个白球)=1−P(A0)−P(A1)
P ( 至 多 取 到 2 个 白 球 ) = P ( A 0 ) + P ( A 1 ) + P ( A 2 ) P(至多取到 2 个白球) = P(A_0) + P(A_1) + P(A_2) P(至多取到2个白球)=P(A0)+P(A1)+P(A2)
例 2: 足球场内23个人(双方队员 11 人加 1 名主裁),至少有两人生日相同的概率为多大?
解: 假设每个人的生日在一年 365 天是等可能的。所以 23 人的生日共有 36 5 23 365^{23} 36523 种可能结果。
先考虑事件 A: “任何两人生日不同”,
要使 A 发生,共有 365 × 364 × . . . × ( 365 − 22 ) 365\times364\times...\times(365-22) 365×364×...×(365−22) 种可能。
因此, P ( A ) = 365 × 364 × . . . × ( 365 − 22 ) 36 5 23 ≈ 0.493 P(A) = \frac{365\times364\times...\times(365-22)}{365^{23}} \approx 0.493 P(A)=36523365×364×...×(365−22)≈0.493
P ( A ‾ ) = 1 − P ( A ) = 0.507 > 0.5 P(\overline{A}) = 1 - P(A) = 0.507 > 0.5 P(A)=1−P(A)=0.507>0.5
例 3: (抽签问题)一袋中有 a 个白球, b 个蓝球,记 a+b=n.设每次摸到各球的概率相等,每次从袋中摸一球,不放回地摸n次。求第 k 次摸到白球的概率。
记 A k = { 第 k 次 摸 到 白 球 } , k = 1 , 2 , . . . , n . 求 P ( A k ) . A_k = \{第 k 次摸到白球\}, k = 1,2,...,n. 求 P(A_k). Ak={第k次摸到白球},k=1,2,...,n.求P(Ak).
解 1. 将 n 个球依次编号为 :1,2,…,n,其中前 a 号是白球。
视 1,2,…,n 的每一个排列为一样本点,则每一样本点等概率。
P ( A k ) = a ( a + b − 1 ) ! ( a + b ) ! = a a + b 与 k 无 关 P(A_k) = \frac{a(a+b-1)!}{(a+b)!} = \frac{a}{a+b} 与 k 无关 P(Ak)=(a+b)!a(a+b−1)!=a+ba与k无关
解 2. 将第 k 次摸到的球号作为一个样本点,由对称性,取到各球的概率相等。
S = { 1 , 2 , . . . , a , a + 1 , . . . , n } S = \{1,2,...,a,a+1,...,n \} S={1,2,...,a,a+1,...,n}
A k = 1 , 2 , . . . , a A_k = {1,2,...,a} Ak=1,2,...,a
⟹ P ( A k ) = a n = a a + b \implies P(A_k)=\frac{a}{n}=\frac{a}{a+b} ⟹P(Ak)=na=a+ba









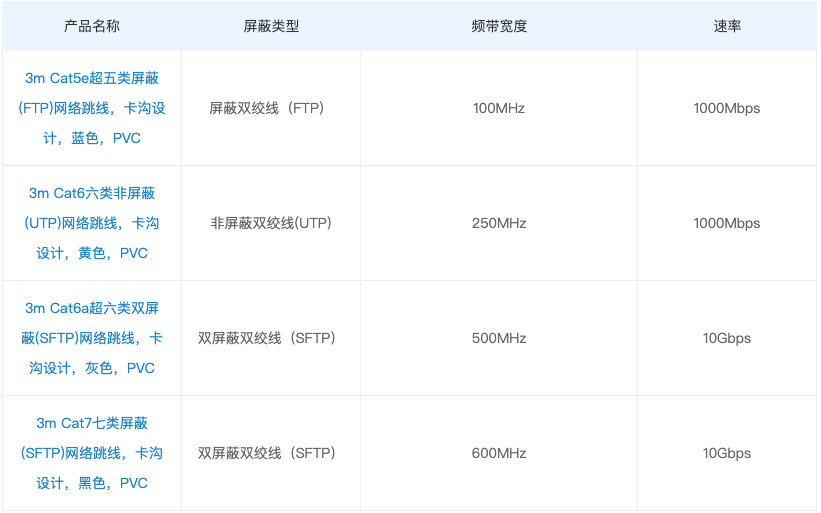

![[4G+5G专题-132]: 传输层 - 以太网电缆的类型(Cat5,Cat5e,Cat6,Cat6a)](https://img-blog.csdnimg.cn/img_convert/28d0fe8566074d316738c3be4545777d.png)