引言

不知道大家还记不记得前面我们分享 支持向量机（SVM）的分析及python实现时说过，当数据遇到线性不可分时，我们可以利用kernel技巧将低维数据映射到高维数据上,从而使得数据线性可分，这是个“升维”操作。那么本章我们就来分享个“降维”操作。

为什么要降维

众所周知，降维的目标就是对输入的数据进行削减，由此剔除数据中的噪声并提高机器学习方法的性能。那么为什么会有降维的操作呢？那是因为高维空间会出现样本稀疏、距离计算困难等问题，这些被我们称作“维数灾难”。缓解维数灾难的一个重要途径就是降维了。首先我们来分享第一个降维算法PCA。
##PCA简单数学原理
主成分分析（Principal Component Analysis，简称PCA）是最常用的一种降维方法。我们有一个假设，即样本点处于一个正交属性空间。存在一个超平面能够将这些样本恰当的表达，同时该超平面还满足如下性质：

• 最近重构型：样本点到这个超平面的距离都足够近
• 最大可分性：样本点在超平面的投影能尽可能分开

基于这两个性质我们就能得到两种等价推导。这里我们不做推导的详细说明（详细过程，请戳：wiki），直接给条件，写出最后的结论。
假定数据样本进行了中心化，即${\sum }_i{x}_i=0$；再假定投影变换后得到的新坐标系为 { w 1 , w 2 , . . . , w d } \{w_1,w_2,...,w_d\} {w1​,w2​,...,wd​}，其中$w_i$是标准正交基向量，即$||w_i|{|}_2=1,w_i^T{w}_j=0,i\ne j$;最终通过一系列推导会得到：
$$X{X}^{T}W=\lambda W$$
于是我们只需对协方差矩阵$X{X}^T$进行特征值分解，将求得的特征值排序：$\lambda_1 \geqslant\lambda_2\geqslant…\geqslant\lambda_d $，再取前$d^{‘}$个特征值对应的特征向量构成$W = (w_1,w_2,…,w_{d^{’}})$。这就是主成分分析的解。

PCA代码实现

那么PCA的伪代码如下：

• 去除平均值（中心化）
• 计算协方差矩阵
• 计算协方差矩阵的特征值和特征向量
• 将特征值从大到小排序
• 保留最上面的N个特征向量
• 将数据转化到上述N个特征向量构建的新空间中
  具体代码如下：

def pca(dataMat, topNfeat=9999999):meanVals = mean(dataMat, axis=0)meanRemoved = dataMat - meanVals #remove meancovMat = cov(meanRemoved, rowvar=0)eigVals,eigVects = linalg.eig(mat(covMat))eigValInd = argsort(eigVals)            #sort, sort goes smallest to largesteigValInd = eigValInd[:-(topNfeat+1):-1]  #cut off unwanted dimensionsredEigVects = eigVects[:,eigValInd]       #reorganize eig vects largest to smallestlowDDataMat = meanRemoved * redEigVects#transform data into new dimensionsreconMat = (lowDDataMat * redEigVects.T) + meanValsreturn lowDDataMat, reconMat

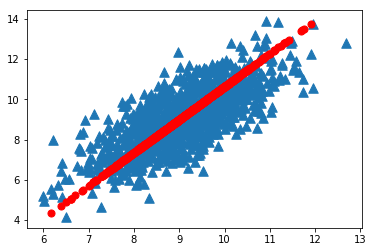
我们采用一个有1000个数据点组成的数据集对其进行PCA降维，运行效果：

import importlib
import pca

importlib.reload(pca)
dataMat = pca.loadDataSet('testSet.txt')
lowDMat,reconMat = pca.pca(dataMat,1)

import numpy as np 
np.shape(lowDMat)

(1000, 1)

import matplotlib
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.add_subplot(111)
ax.scatter(dataMat[:,0].flatten().A[0],dataMat[:,1].flatten().A[0],marker='^',s=90)

<matplotlib.collections.PathCollection at 0x1d8b72b6ac8>

ax.scatter(reconMat[:,0].flatten().A[0],reconMat[:,1].flatten().A[0],marker='o',s=50,c='red')

<matplotlib.collections.PathCollection at 0x1d8b6edb438>

plt.show()

总结

降维技术使得数据变得更易使用，并且它们往往能去除数据中的噪声，使得其他机器学习任务更加精确。