R统计绘图-PCA分析绘图及结果解读(误差线，多边形，双Y轴图、球形检验、KMO和变量筛选等)

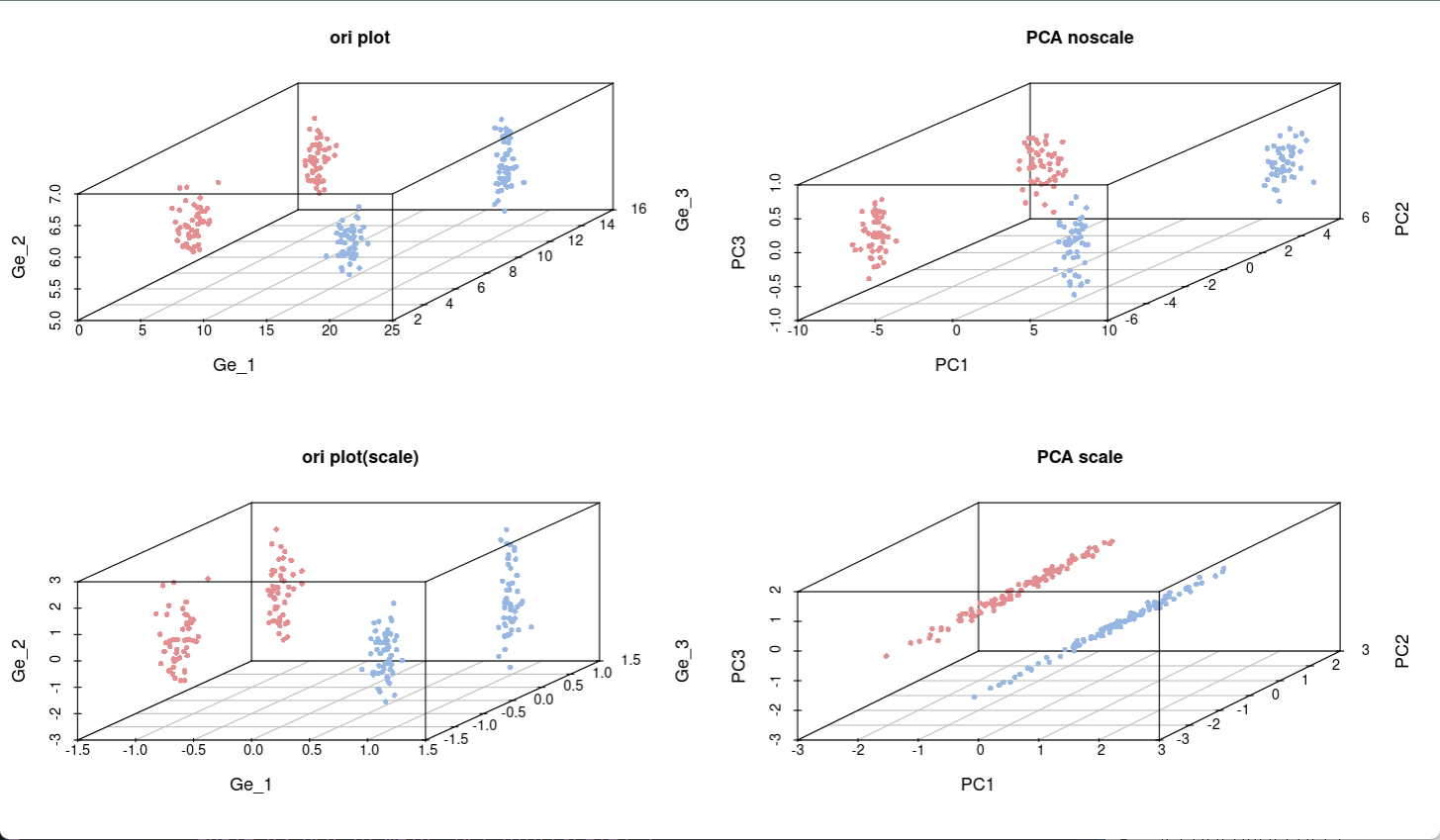
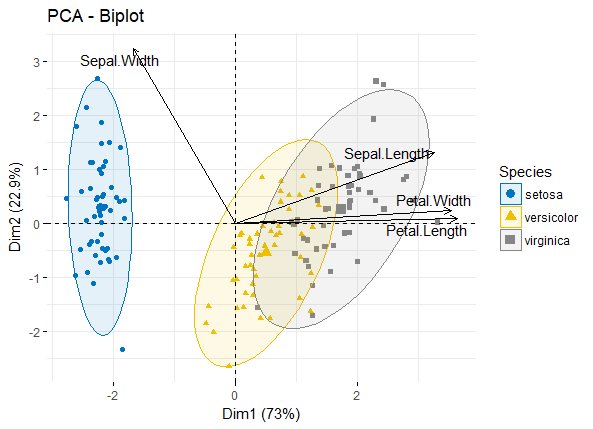
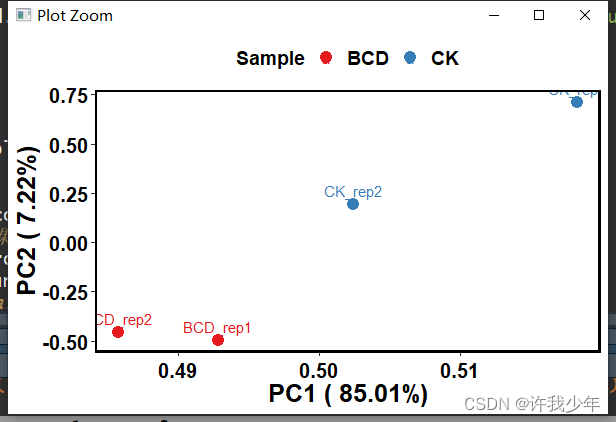
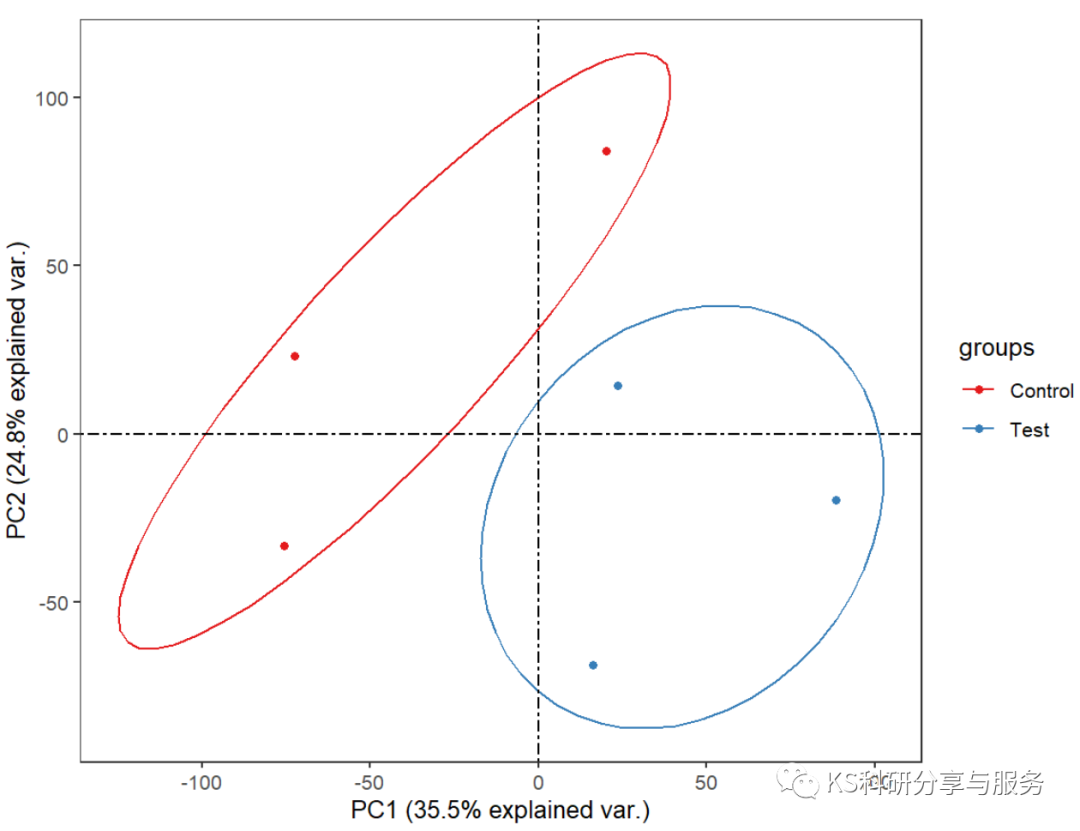
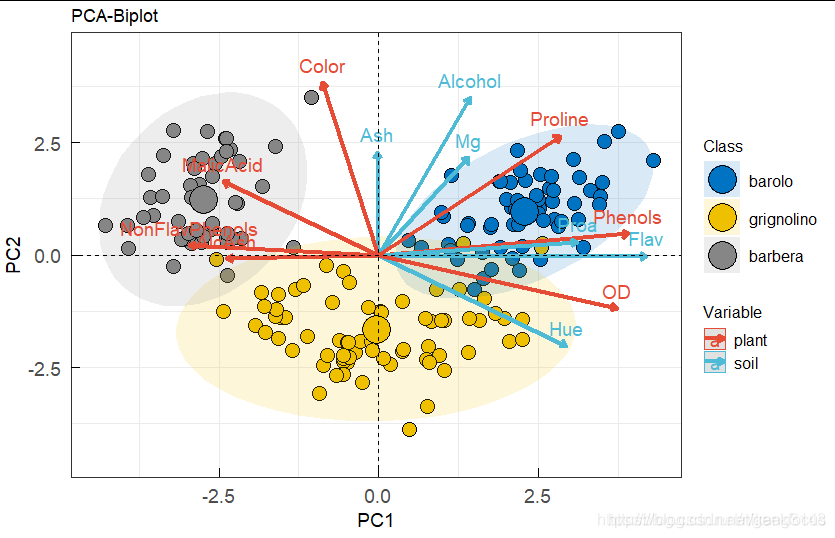
虽然PCA和RDA分析及绘图都写过教程，但是对于结果的解释都没有写的很详细，刚好最近有人询问怎样使用FactoMineR factoextra包进行PCA分析。所以使用R统计绘图-环境因子相关性热图中的不同土壤环境因子数据进行PCA绘图和结果解读推文。

一、数据准备

# 1.1 设置工作路径
#knitr::opts_knit$set(root.dir="D:\\EnvStat\\PCA")# 使用Rmarkdown进行程序运行
Sys.setlocale('LC_ALL','C') # Rmarkdown全局设置
options(stringsAsFactors=F)# R中环境变量设置，防止字符型变量转换为因子
setwd("D:\\EnvStat\\PCA")# 1.2 读入环境因子数据-包含样本和环境因子分类信息
data <- read.table("env.csv", header = T, row.names = 1, sep = ",")
data
dim(data)# 1.3 提取环境因子数据-并将数据转换为数值格式
# apply(data[-1,4:14],2,as.numeric) 表示将数据表按列转换为数值型数据
env = data.frame(data[-1,1:3],apply(data[-1,4:14],2,as.numeric),row.names=rownames(data[-1,]))
###env = data[-1,];env[4:14] = as.numeric(unlist(env[4:14])) # 此代码可以达到上述相同目的
head(env)
dim(env)
## 图2的表可以直接读入
#env=read.csv("env.csv",header = T,row.names = 1,
#sep = ",",comment.char = "",
#stringsAsFactors = F,
#colClasses = c(rep("character",4),rep("numeric",11)))
#head(env) # 查看数据前几行# 1.4 提取环境因子分类信息
type = data.frame(t(data[1,-c(1:3)]))
dim(type)
type # 分类信息只是为了展示，不代表真实分类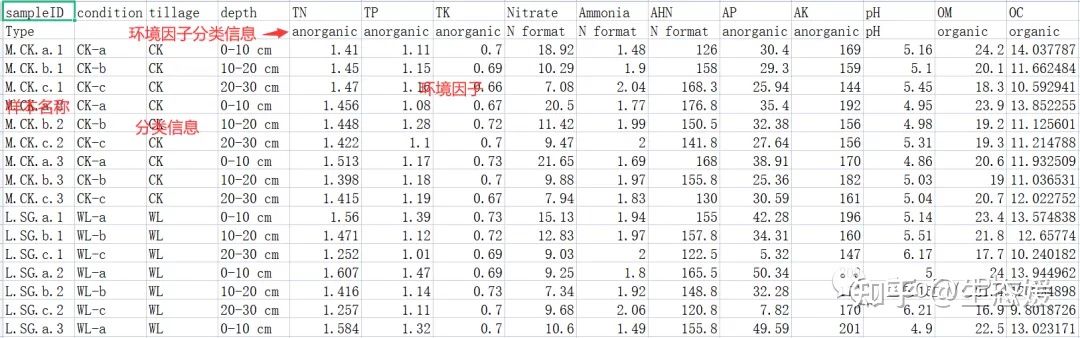

图1|data.csv。环境因子分类信息可以另整理一张表。没有环境因子分类信息就整理为图2格式即可。

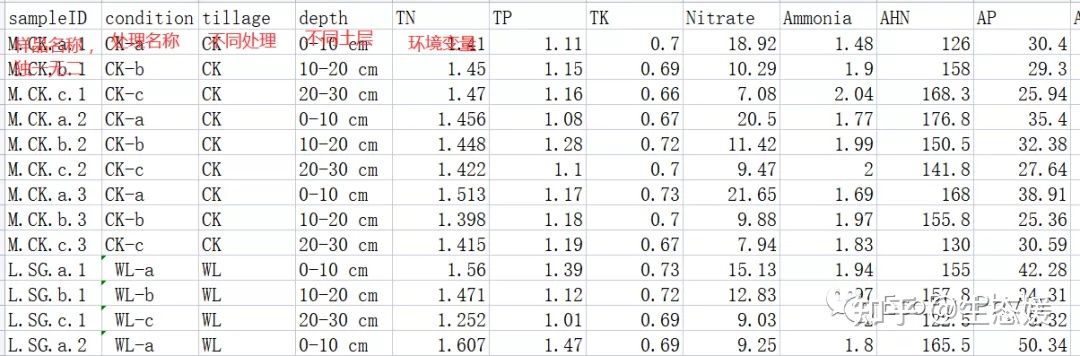
图2|环境因子及分组信息表，env.csv。行为样品名称，列为环境因子名称和分组信息，共有11个环境变量，3个分组信息。

二、主成分分析(PCA)

数据都准备好后，使用FactoMineR中的PCA()函数进行PCA分析，factoextra包可用于提取PCA分析结果信息和绘图(用ggplot2绘图也可)。配套的FactoInvestigate包(http://factominer.free.fr/reporting/index.html)可以自动输出FactoMineR中PCA，MCA和CA分析的结果解释。

# 2.1 调用R包
#install.packages("FactoInvestigate")
#install.packages("htmltools",version="0.5.2")
library(FactoMineR)
library(factoextra) # 用于提取PCA分析结果信息，其实不用也可以。
library(FactoInvestigate)
#browseVignettes("FactoMineR") # 查看帮助文档# 2.2 PCA分析
#res.pca <- PCA(env[4:14], graph = TRUE,axes = c(1,2)) 
##graph = TRUE会默认绘制前两个轴的样本与响应变量PCA图(两张图)。
#page(PCA) # 查看函数代码## 具有附加定性变量的PCA分析：附加样本、定性和定量变量对主成分分析没有贡献，
###坐标来自于基于PCA分析结果的预测值。
res.pca <- PCA(env[2:14], scale.unit = TRUE,# 默认对数据进行scale标准化，最后响应变量间的均值为0，sd=1。##相同尺度的标准化避免了一些变量仅仅因为其较大的度量单位而成为主导变量。使变量具有可比性。ncp = 11, # 结果中默认保留5，nrow(env[-ind.sup,])-1(样本数)和ncol(env[2:14][-c(quanti.sup,quali.sup)])(响应变量数)中的最小值个主成分#ind.sup = 1, # 附加样本，1表示数据表的第一行，不是必须的数据，默认为NULL。附加样本的坐标将根据PCA分析结果进行预测。quanti.sup = NULL, # 附加的定量响应变量数据，不是必须的，默认为NULL。基于PCA分析结果预测坐标。quali.sup = 1:2, # 附加定性变量，分类信息最好不要用数字表示，在行数区间的数字，运行会报错。##1:2表示定性变量在env[2:14]中的列数。不是必须的，默认为NULL。基于PCA分析结果预测坐标，可用于对样本进行分组着色。row.w = NULL, col.w = NULL, # 分别给样本和响应变量设定权重，默认所有样本或所有响应变量的权重都是一样的。默认相当于对变量数据进行了中心化，变量均值接近0。可以设置为1个数字，也可以设置为分别与行数或列数相等的矢量。graph = FALSE)

注：：PCA是基于线性模型的排序方法，因此会涉及数据的中心化和标准化。数据中心化是将原数据减去其均值，中心化后数据的均值为0。样方的中心化是让每个样方的平均值为0，响应变量中心化是让每个响应变量的平均值为0。如果响应变量的量纲不同，响应变量数据就需要标准化。数据的标准化(归一化)是指将数据按照比例缩放，使之所有变量具有相同的尺度，比如常用的Z-score标准化(先对变量进行零中心化，再除以数据标准误差),或者离差标准化(数据减去最小值，再除以最大值与最小值的差值)后数据尺度为[0,1],而MaxAbsScaler绝对值最大标准化(数据除以最大绝对值，不移动中心点。不会将稀疏矩阵变得稠密)后数据尺度为[-1,1]。数据转换方法的选择，需要考虑研究在意的是数据的数值大小变化还是数据变化程度的变化，在意数值本身的变化可以使用原始数据或log转换，在意数据变化程度，则可进行标准化。当数据集中含有离群点，即异常值时，可以用z-score进行标准化，但是标准化后的数据并不理想，因为异常点的特征往往在标准化之后容易失去离群特征。此时可以用RobustScaler方法针对离群点做标准化处理。

FactoInvestigate包的Investigate()可以自动输出FactoMineR包PCA分析的结果解释,输出文件可以是word,html和PDF。默认输出离群值，主成分对样本方差的解释度检测，维度描述,样本聚类及对每个cluster贡献高的变量等信息。

# 2.3 FactoInvestigate包的Investigate()输出结果报告
#?Investigate # 查看函数帮助信息
Investigate(res.pca,file = "Investigate.Rmd",openFile = FALSE,document = c("word_document"))

注：输出的结果包括Investigate.docx或Workspace.RData和Investigate.Rmd。Investigate.docx是word版PCA分析结果报告与结果解读，写的很详细。如果因为某种原因输出报告文件报错(常见htmltools包版本或LaTeX报错)，就会输出Workspace.RData和Investigate.Rmd，包含分析代码和绘图结果，两者放在在同一目录，运行Investigate.Rmd，可以复现PCA分析结果。图不是太好看，可以输出数据自己画。

# 2.4 PCA分析结果的输出数据介绍
str(res.pca)# 输出一个list数据集
summary(res.pca,ncp=2,nbelements=Inf) # nbelements=Inf，输出所有结果## 2.4.1 主成分(PC)特征值
## eigenvalue：特征值可以用来确定在PCA之后要保留的主成分的数量
get_eigenvalue(res.pca) # 11个主成分累计代表的样本方差为100%。
sum(res.pca$eig[,1]) # 所有主成分所表示的总方差为11(11个原始变量)。
res.pca$eig # 包含3列数据，每个主成分的特征值，方差百分比和累积方差百分比。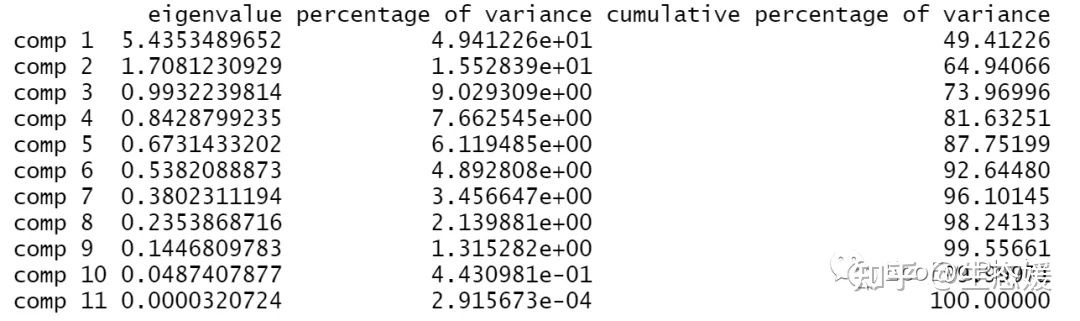

图3|主成分特征值，res.pca$eig。特征值表示每个主成分保留的原始变量的变化量。特征值从高到低排序，PC1表示变量变化最大的方向。选择代表方差>1(特征值>1表示PC比标准化数据中的一个原始变量解释的方差更大。数据未标准化或变量权重不同，不能这样进行选择),此处累计方差解释量~65%(>80%更好)的PC1和PC2进行可视化和后续分析(也可以选择累计方差解释率超过一定阈值的PC用作后续分析)。

## 2.4.2 样本PCA输出数据
res.pca$ind # 包含所有样本的输出结果的矩阵列表
#get_pca_ind(res.pca) # 可以使用factoextra包的函数提取样本输出数据。res.pca$ind$coord # 样本在PC的坐标=左奇异值/sqrt(eig)
res.pca$ind$cos2 # 样本坐标的平方/样本Euclid(L2)范数的平方(标准化数据)。
## 未标准化数据，样本1的cos2=ind1.coord^2/每个个体与PCA重心之间的平方距离(d2)。d2=([(Var1-Var1.mean)/Var1.sd]^2+...+[(Varn-Varn.mean)/Varn.sd]^2)
res.pca$ind$contrib # 所有样本对主成分的贡献度(%)=(res.pca$ind$coord^2)*100/eig^2/样本数
res.pca$ind$dist # 变量标准化之后，样本L2范数(Euclid范数)，即每个样本包含变量的(值平方*变量权重)的和的平方根
##可反应样本间距离。dist值差异越大，样本相似性越小。

注：L2范数指向量中所有数据平方和的平方根。范数介绍：https://blog.csdn.net/a493823882/article/details/80569888

## 2.4.3 响应变量PCA输出数据
res.pca$var # 包含所有响应变量相关结果的矩阵列表
#get_pca_var(res.pca) # 可以使用factoextra包的函数提取响应变量输出数据。res.pca$var$coord # 所有响应变量(这里是环境因子)的坐标，等于右奇异值*特征根的平方根=载荷值(主成分能代表的响应变量的方差)*特征根(主成分的标准误差)。res.pca$var$cor # 样本权重一样时，每个响应变量与轴的相关性=响应变量坐标/(变量值的平方和/样本数的平方根)。绝对值越大，表明相关性越强,正负表示方向。res.pca$var$cos2 # 所有响应变量与轴相关性的平方，等于res.pca$var$cor^2。res.pca$var$contrib # 响应变量对每个主成分的方差贡献值=(var$cos2*100)/apply(res.pca$var$cos2,2,sum)

注：PCA()也计算了响应变量的dist，计算方式为dist2.var <- as.vector(crossprod(rep(1, nrow(X)), as.matrix(X^2 * row.w)))。X为标准化后的数据矩阵，row.w=样本权重/(样本权重之和)，crossprod()内积运算。

# 2.4.4 附加变量预测输出结果：附加样本、定性和定量变量对主成分没有任何贡献。
res.pca$quali.sup # 附加定性变量中每个分类的输出结果。最后输出的报告里会基于Wilks test分析那些定性变量能更好的解释样本之间的差异。
res.pca$quali.sup$coord # 定性变量中每个分类的坐标
res.pca$quali.sup$cos2 # 定性变量中每个分类被主成分代表的部分
res.pca$quali.sup$v.test # 定性变量中每个分类Normal distribution准则
res.pca$quali.sup$eta2 # 定性变量与每个主成分的相关性系数的平方
res.pca$quali.sup$dist # 可用于比较分类变量个水平间的距离。

图4|附加变量预测输出结果。

# 2.4.5 其它输出数据
library(rstatix)
#env[4:11] %>% get_summary_stats(type="mean_sd")
res.pca$call$centre # 响应变量的均值
res.pca$call$ecart.type # 响应变量的标准误差
res.pca$call$row.w.init # 样本权重
res.pca$call$col.w # 响应变量权重
res.pca$call$ncp # 主成分维度
#env[4:11] %>% group_by(env$tillage) %>% get_summary_stats(type="mean")
res.pca$call$quali.sup # 附加定性变量统计值
res.pca$call$X # 原始数据
res.pca$call$call # 运行代码

三、PCA分析结果绘图

factoextra包中的绘图函数fviz_pca_biplot()可以用于绘制PCA双序图。fviz()是ggpubr包中ggscatter()函数的包装器，可以与ggpubr的函数联用。也可用提取的数据使用ggplot2绘图。这里先使用ggplot2绘图，下篇文章介绍factoextra包中的绘图函数。

3.1 提取绘图数据

FactoInvestigate包的Investigate()默认输出的图很多，但是信息没有整合，而且很多细节还需要调整。这里提取数据，自己使用ggplot2进行绘图。

# 3.1.1 提取样本坐标
# get_pca_ind(res.pca) # factoextra提取分析结果，可以很方便的提取prcomp()和princomp()函数的样本PCA分析结果。
sam=data.frame(res.pca$ind$coord)
sam
sam=data.frame(sam[1:2],env[1:3]) # 添加样本分组信息
sam# 3.1.2 提取特征值-每个主成分对样本方差的解释度。
fviz_eig(res.pca,addlabels = TRUE) # 对每个主成分对方差的解释度绘制柱形图。
#fviz_screeplot(res.pca)# 对每个主成分对方差的解释度绘制柱形图。
eig.val <- get_eigenvalue(res.pca) # get_eig(res.pca)效果一样，提出的是res.pca$eig矩阵中数据。
eig.val
## 提取前两个主成分是特征值，并保留两位小数点。
PC1=round(eig.val[1,2],2)
PC2=round(eig.val[2,2],2)
PC1
PC2# 3.1.3 提取响应变量坐标值
var <- get_pca_var(res.pca) # 提取响应变量结果矩阵列表。
res=data.frame(var$coord) # res=data.frame(res$var$coord),效果一样。
res
type
res$type = type[match(rownames(type),rownames(res)),1] # 添加环境因子分类信息
res# 3.1.4 提取附加定性变量的坐标值
quali = data.frame(res.pca$quali.sup$coord)
quali

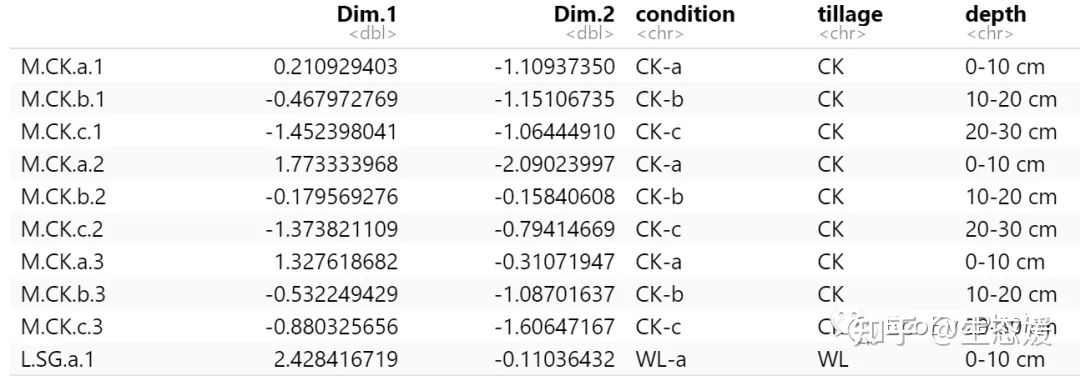
图5|样本坐标信息表，sam。

factoextra包中提取样本、变量和特征根PCA分析结果的函数，常用于prcomp()和princomp()分析结果提取。

# 3.1.5 prcomp()和princomp()主成分分析
prcmp = prcomp(env[4:14], scale =TRUE)
princmp= princomp(env[4:14], cor = TRUE, scores = TRUE) # cor = TRUE表示对数据进行标准化，scores=TRUE表示输出所有PC结果。
prcmp$sdev # 特征根=princmp$sdev
prcmp$rotation # 变量载荷矩阵(列就为PC的特征向量)=princmp$loadings，可用于预测附加样本坐标。
## 载荷值*特征根得出变量在每个主成分的坐标
prcmp$center# 变量均值=princmp$center
prcmp$scale # 变量的standard deviations=princmp$scale
prcmp$x # 样本观察值(坐标)=princmp$scoresget_pca_ind(prcmp) # 提取样本坐标和代表性等信息。
get_pca_var(prcmp) # 提取变量坐标和代表性等信息。
get_eigenvalue(prcmp) # 提取主成分特征值、解释度和累积解释度。

注：prcomp()和princomp()提取的结果与PCA()有些微差别，分析是对数据的处理有些微差异，prcomp()和princomp()标准误差计算用的是n(样本数)-1，而PCA()使用的n。推荐使用prcomp()和princomp()分析后，使用factoextra包函数提取坐标等信息。PCA()不会输出变量载荷矩阵。

3.2 绘图

这里将以不同颜色(tillage)的形状(