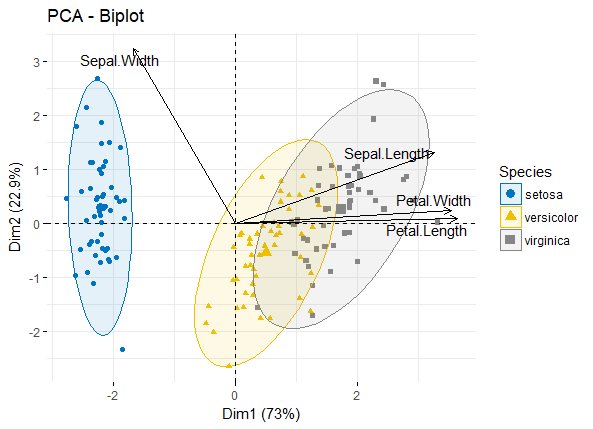
学习笔记的主要内容是在R语言中利用ggplot2进行PCA分析和绘图,包括简单分析与操作流程,对比不同方式得到的结果差异,提供脚本代码供练习.
PCA分析的原理
在处理基因差异表达数据时,有时候需要分析其中因素的影响最大,判断结果的关系,这个时候可以用PCA分析法,之前发过一篇PCA分析的简介和数学原理解析,如果有兴趣点击这里查看,今天的笔记主要围绕实际操作过程进行分享。笔者学习时参考易汉博的教程,感觉这个教程挺好的,推荐给大家,也可以在学习过程中一起交流。
PCA分析示例
创建演示数据
count <- 100 #设置变量个数为100
Ge_1a <- rnorm(count,4,0.6) #生成100个服从均值为4标准差为0.6正态分布的数字
Ge_1b <- rnorm(count,19,0.4)
gro_a <- rep('a',count) #生成100个a,代表a组
gro_b <- rep('b',count)
演示数据为Ge_1的表达量(每个基因包括两组类型的值各100个,且两个组的表达量有差异),接下来创建根据数据创建矩阵,设置样本的名称标签,添加新列R,并生成一个表格输出基因在200个样本中的表达量,每一行为一个样品,每一列为基因的表达值。
c_data <- data.frame(Ge_1=c(Ge_1a,Ge_1b),Group=c(gro_a,gro_b))
label <- c(paste0(gro_a,1:count),paste0(gro_b,1:count))
row.names(c_data) <- labelc_data$R <- rep(0,count*2)
kable(headTail(c_data),booktabs=TRUE,caption="Expr Profile For Ge_1 in 200 samples")
生成了200行3列的表格数据,结果如下:
Table: Expr Profile For Ge_1 in 200 samples
| |Ge_1 |Group |R |
|:----|:-----|:-----|:---|
|a1 |4.77 |a |0 |
|a2 |4.13 |a |0 |
|a3 |4.15 |a |0 |
|a4 |4.04 |a |0 |
|... |... |NA |... |
|b97 |18.93 |b |0 |
|b98 |18.06 |b |0 |
|b99 |18.74 |b |0 |
|b100 |19.52 |b |0 |
加载R包
library(knitr)
library(psych)
library(reshape2)
library(ggplot2)
library(ggbeeswarm)
library(scatterplot3d)
library(useful)
library(ggfortify)
需要加载上述R包,如果没有请先安装后载入R包。
绘制图像
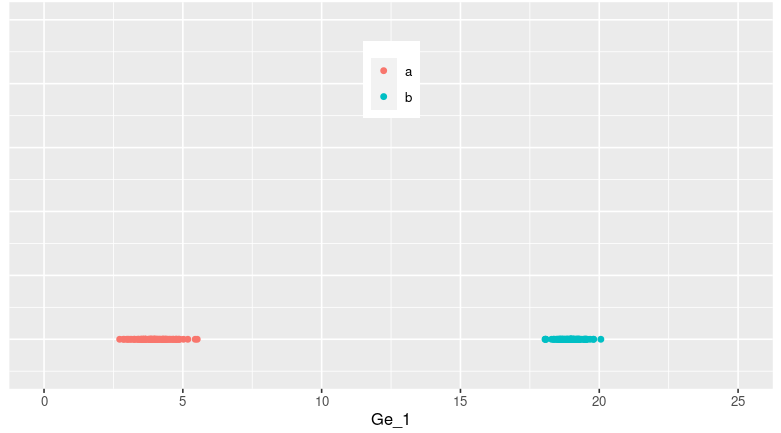
p <- ggplot(c_data,aes(Ge_1,R)) + geom_quasirandom(aes(color=factor(Group))) +theme(legend.position = c(0.5,0.8)) +theme(legend.title = element_blank()) +scale_fill_discrete(name="Group") +theme(axis.line.y=element_blank(),axis.text.y=element_blank(),axis.ticks.y=element_blank(),axis.title.y=element_blank()) +ylim(-0.5,5) + xlim(0,25)
p
利用ggplot函数进行绘图,发现200个样本在Ge1基因表达量上分为了两类(原因是刚刚生成数据时分成了两个不同类型的组,表达量存在差异)
添加一个基因
刚刚是只有Ge1的情况,接下来再创建一个Ge_2(方法和刚刚类似),看看两个基因时情况会发生什么变化?
创建一组均值为6标准差为0.3的正态分布随机数据,并设置行名构建矩阵,输出表达矩阵。需要注意的是:Ge_2的表达量保持稳定(a组和b组的表达水平相当),不像Ge_1存在表达量差异。
> count <- 100
> Ge_2a <- rnorm(count,6,0.3)
> Ge_2b <- rnorm(count,6,0.3)
> c2_data <- data.frame(Ge_1=c(Ge_1a,Ge_1b),Ge_2=c(Ge_2a,Ge_2b),
+ Group=c(gro_a,gro_b))
> row.names(c2_data) <- label
> kable(headTail(c2_data),booktabs=T,
+ caption="Expression for Ge_1 and Ge_2 in 200 samples")Table: Expression for Ge_1 and Ge_2 in 200 samples
| |Ge_1 |Ge_2 |Group |
|:----|:-----|:----|:-----|
|a1 |4.77 |5.71 |a |
|a2 |4.13 |5.65 |a |
|a3 |4.15 |6.38 |a |
|a4 |4.04 |5.88 |a |
|... |... |... |NA |
|b97 |18.93 |6.06 |b |
|b98 |18.06 |6.29 |b |
|b99 |18.74 |5.78 |b |
|b100 |19.52 |5.87 |b |
利用ggplot函数作图,数据为c2data,此时能显示出Ge1和Ge2的分布情况,可以看出在Ge_1(x轴)上分成了两类,而Ge_2上分类趋势很小(因为Ge_2本身就没什么差异分组)
p <- ggplot(c2_data,aes(Ge_1,Ge_2)) +geom_point(aes(color=factor(Group))) +theme(legend.position = c(0.5,0.8)) +theme(legend.title = element_blank()) +ylim(0,10)+xlim(0,25)
p

再添加一个基因
刚刚是两个基因,现在再加一个Ge_3,这个基因的表达量差异设置的更大一些,设置该基因分成两个组,而且每个组的表达量也存在两种类型,所以这个基因对样本分类的作用更大。
> count <- 100
> Ge_3a <- c(rnorm(count/2,6,0.4),rnorm(count/2,14,0.3))
> Ge_3b <- c(rnorm(count/2,14,0.3),rnorm(count/2,4,0.4))
> data_3 <- data.frame(Ge_1=c(Ge_1a,Ge_1b),
+ Ge_2=c(Ge_2a,Ge_2b),
+ Ge_3=c(Ge_3a,Ge_3b),
+ Group=c(gro_a,gro_b))
> data_3 <- as.data.frame(data_3)
> data_3$Group <- as.factor(data_3$Group)
> row.names(data_3) <- label
>
> kable(headTail(data_3),booktabs=T,caption = "Expression 3 Genes in 200 samples")Table: Expression 3 Genes in 200 samples
| |Ge_1 |Ge_2 |Ge_3 |Group |
|:----|:-----|:----|:----|:-----|
|a1 |4.77 |5.71 |5.61 |a |
|a2 |4.13 |5.65 |6.38 |a |
|a3 |4.15 |6.38 |6.47 |a |
|a4 |4.04 |5.88 |5.82 |a |
|... |... |... |... |NA |
|b97 |18.93 |6.06 |3.57 |b |
|b98 |18.06 |6.29 |4.37 |b |
|b99 |18.74 |5.78 |4.18 |b |
|b100 |19.52 |5.87 |4.82 |b |
生成一组颜色变量,用于区分不同类别。每个数据向底面做垂直投影,可以看出在x轴方向(Ge_1)和z轴(Ge_3)上投影时在不同位置分成两类,而在y轴(Ge_2)上投影位于同一区域,所以可以看出Ge_2对样本分类的贡献度最小。
colorl <- c("#E19F90", "#96B4E9")
colors <- colorl[as.numeric(data_3$Group)]
scatterplot3d(data_3[,1:3],color=colors,xlim=c(0,24),ylim=c(0,24),zlim=c(0,24),type="h",angle=45,pch=16)
legend("top",legend=levels(data_3$Group),col=colorl,pch=16,xpd=T,horiz=T)
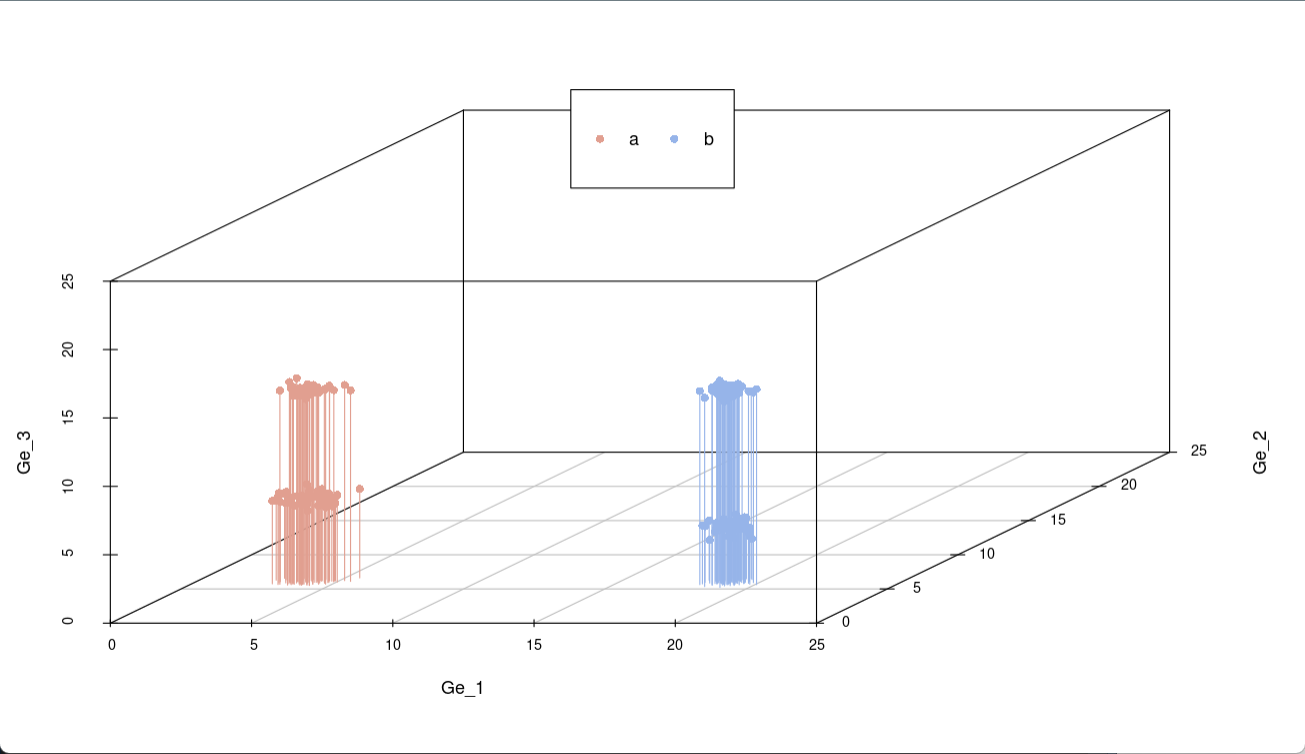
通过上面的演示,已经基本了解PCA的作用了,通过PCA分析能将不同基因在不同样本中的表达量分成几类,接下来,用简单的例子来演示流程。
PCA的实现流程
使用上面创建的data_3数据来进行后续操作。首先生成表达矩阵,包含3个基因在200个样本中的表达情况。
> kable(headTail(data_3),booktabs=T,caption = "Expression 3Gene in 200 samples")
Table: Expression 3Gene in 200 samples
| |Ge_1 |Ge_2 |Ge_3 |Group |
|:----|:-----|:----|:----|:-----|
|a1 |4.77 |5.71 |5.61 |a |
|a2 |4.13 |5.65 |6.38 |a |
|a3 |4.15 |6.38 |6.47 |a |
|a4 |4.04 |5.88 |5.82 |a |
|... |... |... |... |NA |
|b97 |18.93 |6.06 |3.57 |b |
|b98 |18.06 |6.29 |4.37 |b |
|b99 |18.74 |5.78 |4.18 |b |
|b100 |19.52 |5.87 |4.82 |b |
# 对数据进行标准化处理
> data_3_cs <- scale(data_3[,1:3],center = T,scale = T)
> kable(headTail(data_3_cs),booktabs=T,caption = "norm Expression 3 gene in 200 samples")
上面的代码是对数据进行标准化和中心化处理(使数据的差异变化幅度在同一水平),将数据转化为均值为0且标准差为1的新数据集。
Table: norm Expression 3 gene in 200 samples| |Ge_1 |Ge_2 |Ge_3 |
|:----|:-----|:-----|:-----|
|a1 |-0.89 |-1 |-0.87 |
|a2 |-0.98 |-1.22 |-0.7 |
|a3 |-0.97 |1.41 |-0.68 |
|a4 |-0.99 |-0.37 |-0.82 |
|... |... |... |... |
|b97 |0.99 |0.25 |-1.32 |
|b98 |0.88 |1.08 |-1.14 |
|b99 |0.97 |-0.73 |-1.18 |
|b100 |1.07 |-0.44 |-1.04 |
> data_3_cs_cov <- cov(data_3_cs)
> kable(data_3_cs_cov,booktabs=T,
+ caption = "cov for 3 gene in 200 samples")
上面的代码生成协方差矩阵,计算3个基因在200个样本中表达数据的协方差。
Table: cov for 3 gene in 200 samples| | Ge_1| Ge_2| Ge_3|
|:----|----------:|----------:|----------:|
|Ge_1 | 1.0000000| -0.0808226| -0.1181946|
|Ge_2 | -0.0808226| 1.0000000| -0.0106916|
|Ge_3 | -0.1181946| -0.0106916| 1.0000000|
> data_3_cs_cov_e <- eigen(data_3_cs_cov)
#求解特征值和特征向量
> data_3_cs_cov_e$values #特征值
> [1] 1.1383477 1.0099558 0.8516964
> data_3_cs_cov_e$vectors #特征向量
> [,1] [,2] [,3]
> [1,] 0.7189945 0.02734216 -0.6944778
> [2,] -0.3748044 -0.82622441 -0.4205650
> [3,] -0.5852936 0.56267720 -0.5838028
上面的代码得到特征值和特征变量,下面的代码用于产生新矩阵。
> pc_select <- 3
> label <- paste0("PC",c(1:pc_select))
> data_3_n <- data_3_cs %*% data_3_cs_cov_e$vectors[,1:pc_select] #%*%表示矩阵相乘
> colnames(data_3_n) <- label
> kable(headTail(data_3_n),booktabs=T,
+ caption = "PCA gene matrix for 3 gene in 200 samples")Table: PCA gene matrix for 3 gene in 200 samples| |PC1 |PC2 |PC3 |
|:----|:-----|:-----|:-----|
|a1 |0.24 |0.31 |1.55 |
|a2 |0.16 |0.59 |1.6 |
|a3 |-0.83 |-1.57 |0.48 |
|a4 |-0.09 |-0.18 |1.32 |
|... |... |... |... |
|b97 |1.39 |-0.92 |-0.02 |
|b98 |0.89 |-1.51 |-0.4 |
|b99 |1.66 |-0.03 |0.33 |
|b100 |1.54 |-0.19 |0.05 |
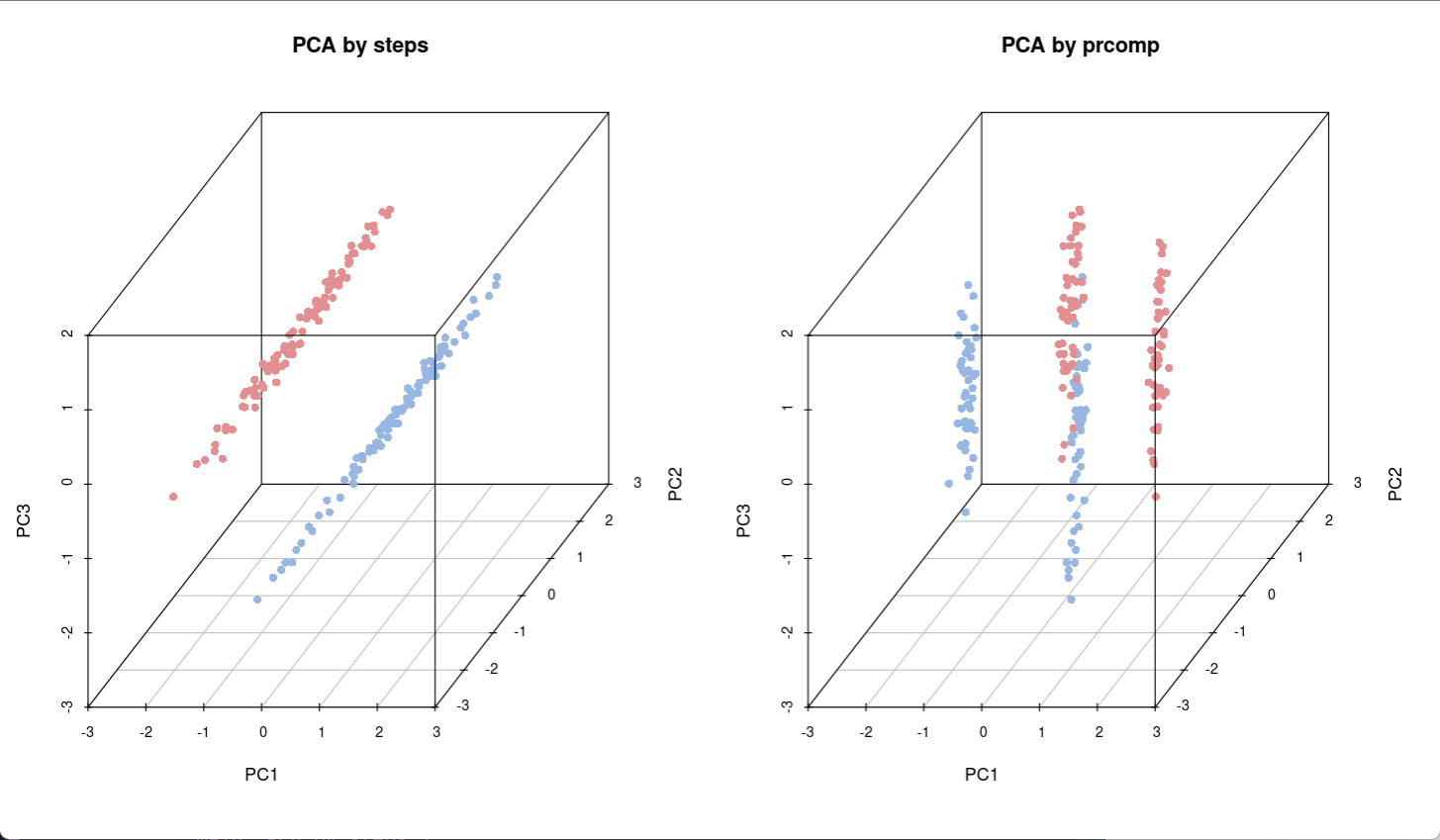
接下来,比较两种方式对样本的聚类差异情况,设置工作区同时输出两个图,并使用scatterplot3d进行绘图。
colorl <- c("#E38F92","#97B6E1")
colors <- colorl[as.numeric(data_3$Group)]par(mfrow=c(1,2)) #图片输出区为一行两图的布局scatterplot3d(data_3[,1:3],color = colors,angle=45,pch=16,main="before data")# 生成图例legend("top",legend = levels(data_3$Group),col=colorl,pch=16,xpd=T,horiz = T)
scatterplot3d(data_3_n,color=colors,angle = 45,pch=16,main="after data")

通过对比上图,可以发现两种数据处理方式形成的样品分组情况不同,在处理后数据右图中,样本的分散程度更大,笔者的理解是其变化特征显示的更广泛,相比左图能够读取更多信息,处理后效果更好(可能是因为此时变量间非线性相关)。
利用prcomp进行PCA分析
pca_data_3 <- prcomp(data_3[,1:3],center=T,scale=T)
str(pca_data_3)
上面的代码对data_3数据进行处理,得到新数据,接着查看一下pca_data_3的数据信息摘要。
List of 5$ sdev : num [1:3] 1.067 1.005 0.923$ rotation: num [1:3, 1:3] -0.719 0.3748 0.5853 0.0273 -0.8262 .....- attr(*, "dimnames")=List of 2.. ..$ : chr [1:3] "Ge_1" "Ge_2" "Ge_3".. ..$ : chr [1:3] "PC1" "PC2" "PC3"$ center : Named num [1:3] 11.47 5.99 9.55..- attr(*, "names")= chr [1:3] "Ge_1" "Ge_2" "Ge_3"$ scale : Named num [1:3] 7.52 0.277 4.548..- attr(*, "names")= chr [1:3] "Ge_1" "Ge_2" "Ge_3"$ x : num [1:200, 1:3] -0.2399 -0.1632 0.833 0.0905 0.3406 .....- attr(*, "dimnames")=List of 2.. ..$ : chr [1:200] "a1" "a2" "a3" "a4" ..... ..$ : chr [1:3] "PC1" "PC2" "PC3"- attr(*, "class")= chr "prcomp"
生成新的数据包含五个变量,按照之前的方法对其进行处理。
data_pca_n <- pca_data_3$x
kable(headTail(data_pca_n),booktabs=T,caption = "PCA gene matrix")
得到prcomp方式的基因表达矩阵,此时存在三个主成分(PC1、2、3)。
Table: PCA gene matrix
| |PC1 |PC2 |PC3 |
|:----|:-----|:-----|:-----|
|a1 |-0.24 |0.31 |1.55 |
|a2 |-0.16 |0.59 |1.6 |
|a3 |0.83 |-1.57 |0.48 |
|a4 |0.09 |-0.18 |1.32 |
|... |... |... |... |
|b97 |-1.39 |-0.92 |-0.02 |
|b98 |-0.89 |-1.51 |-0.4 |
|b99 |-1.66 |-0.03 |0.33 |
|b100 |-1.54 |-0.19 |0.05 |
# 查看特征向量
> pca_data_3$rotationPC1 PC2 PC3
Ge_1 -0.7189945 0.02734216 -0.6944778
Ge_2 0.3748044 -0.82622441 -0.4205650
Ge_3 0.5852936 0.56267720 -0.5838028
接下来,比较两种方式实现PCA分析的结果差异,左图是手动方式,右图是利用prcomp方式,可以看出两种结果具有差异性。
scatterplot3d(data_3_n,color=colors,angle=45,pch=16,main="PCA by steps")
scatterplot3d(data_pca_n,color=colors,angle=45,pch=16,main="PCA by prcomp")
创建PCA计算函数
在R语言中自定义一个函数ct_PCA,用于计算处理PCA数据(参数设置对原始数据进行标准化和中心化)
ct_PCA <- function(data,center=T,scale=T){data_norm <- scale(data, center=center, scale=scale)data_norm_cov <- crossprod(as.matrix(data_norm)) / (nrow(data_norm)-1)data_eigen <- eigen(data_norm_cov)rotation <- data_eigen$vectorslabel <- paste0('PC', c(1:ncol(rotation)))colnames(rotation) <- labelsdev <- sqrt(data_eigen$values)data_new <- data_norm %*% rotationcolnames(data_new) <- labelct_pca <- list('rotation'=rotation, 'x'=data_new, 'sdev'=sdev)return(ct_pca)
}
标准化scale操作是指将数据的差异程度相对化,消除固有差异幅度的影响,从同一衡量标准下判断数据的差异性,接下来,分别演示不经过标准化处理和进行标准化处理的结果。
data_pca_noscale_step <- ct_PCA(data_3[,1:3],center=T,scale = F)
#只中心化,不标准化
data_pca_noscale_step$rotation #查看特征向量PC1 PC2 PC3
[1,] 0.993858995 -0.110611181 -0.003076602
[2,] -0.002918535 0.001590917 -0.999994476
[3,] -0.110615464 -0.993862483 -0.001258325
data_pca_noscale_pc <- data_pca_noscale_step$x
利用刚才生成的四种数据,生成四个不同类型的结果图:
par(mfrow=c(2,2)) #设置输出区为2行2列排版,同时输出4副图
scatterplot3d(data_3[,c(1,3,2)],color=colors,angle=45,pch=16,main="ori plot")
scatterplot3d(data_pca_noscale_pc,color=colors,angle=45,pch=16,main="PCA noscale")
scatterplot3d(data_3_cs[,c(1,3,2)],color=colors,angle=45,pch=16,main="ori plot(scale)")
scatterplot3d(data_3_n,color=colors,angle=45,pch=16,main="PCA scale")
依次生成4副图,可以看出上面两张图(没有scale标准化)的分布比较秘籍,而经过scale处理之后数据的分散程度更高(下面两张图),说明标准化处理后数据的相对变化幅度信息被保留,差异细节更清晰,这也是PCA分析的目的所在。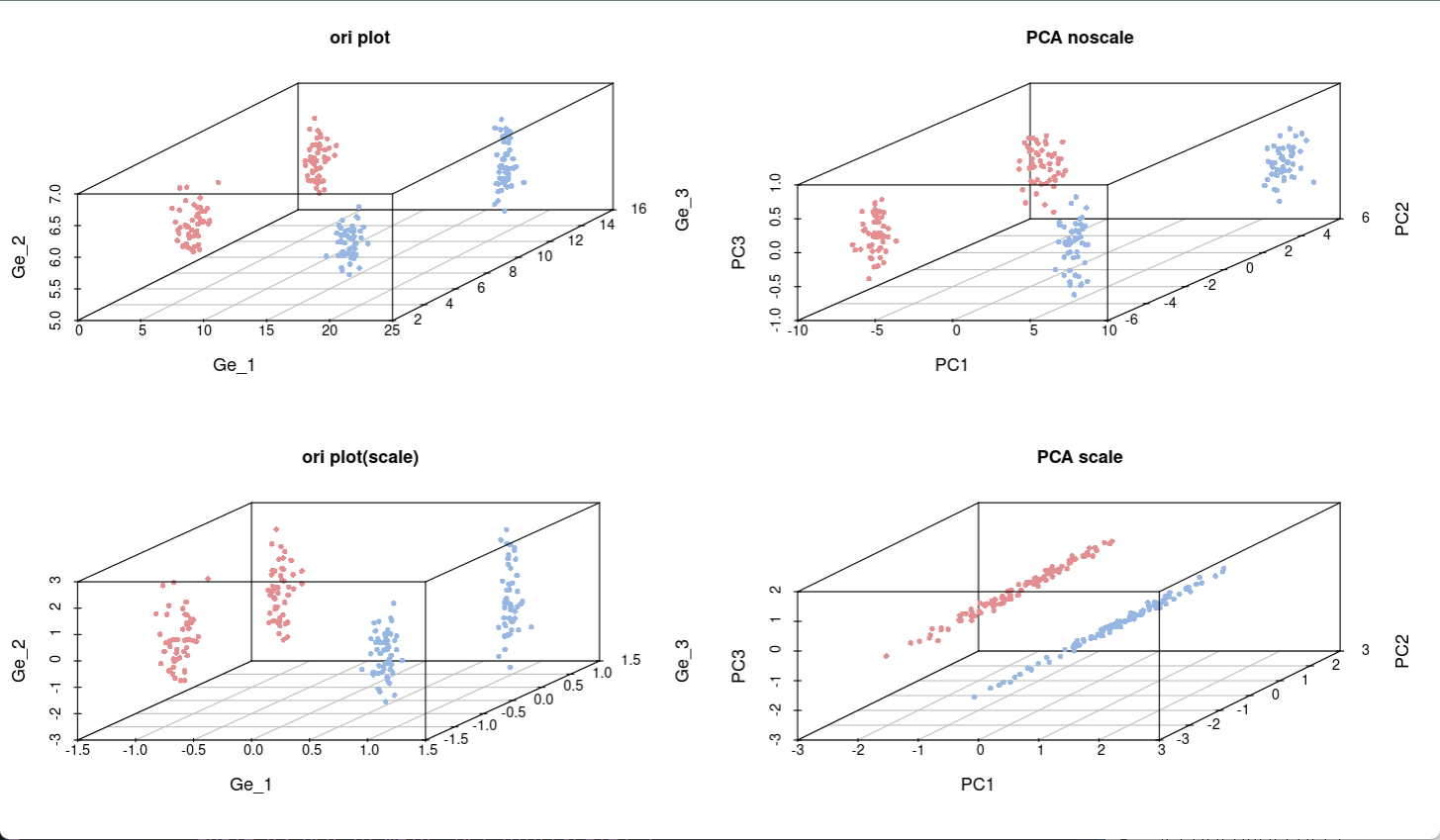
本文中所有代码已整理打包,下载链接:
https://down.jewin.love/?f=/Rscript/PCA.R
参考资料:http://www.ehbio.com
本文由mdnice多平台发布